决策树-机器学习实战

决策树

  决策树模型是一种描述对实例进行分类的树形结构，决策树由节点和有向边组成，节点有两种类型：内部节点和叶节点。内部节点表示一个特征或属性，叶节点表示一个类。
  通常决策树的学习包括3个步骤：特征选择、决策树的生成和决策树的修剪。
  特征选择：选取对训练数据具有分类能力的特征
  通常的准则是信息增益或者信息增益比

1. 信息增益

熵：表示随机变量不确定性的度量。
  设X是一个取有限个值得离散随机变量，其概率分布为：$P(X=x_i) = p_i , i=1,2,...n$, 则X的熵定义为：$H(X) = - \sum_{i=1}^n p_i log p_i$。
熵越大，随机变量的不确定性越大。
计算给定数据集的熵demo：

from math import log

def calcShannonEnt(dataSet):
    #实例总数
    numEntries = len(dataSet)
    #创建字典
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        #记录每个类别出现的次数
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        #计算每个类别出现的概率
        prob = float(labelCounts[key])/numEntries
        #计算熵
        shannonEnt -= prob * log(prob,2)
    return shannonEnt

def createDataSet():
    dataSet = [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels

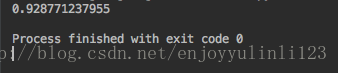
myDat,labels = createDataSet()
print calcShannonEnt(myDat)

输出结果：

条件熵：$H(Y | X)$ 表示在已知随机变量X的条件下随机变量Y的不确定性。
$H(Y|X) = - \sum_{i=1}^n p_i H(Y|X=x_i)$。

信息增益： $g(D,A) = H(D) - H(D | A)$
  经验熵 $H(D)$ 表示对数据集D进行分类的不确定性，经验条件熵$H(D | A)$表示在特征A给定的条件下对数据集D进行分类的不确定性。两者的差为信息增益，表示由于特征A而使得对数据集D的分类不确定减少的程度。

2.划分数据集

  对每个特征划分数据集的结果计算一次信息熵, 然后判断按照哪个特征划分数据集是最好的划分方式

#按照给定的特征划分数据集
def splitDataSet(dataSet, axis, value):
    #新建list
    retDataSet = []
    for featVec in dataSet:
        #抽取符合特征的数据
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

注意：

• Python语言不用考虑内存分配问题 。

  Python语言在函数中传递的是列表的引用, 在函数内部对列表对象的修改, 将会影响该列表对象的整个生存周期。为了消除这个不良影响 ,我们需要在函数的开始声明一个新列表对象。

• list.extend()和 list.append()区别
  
  执行a.append(b)结果为包含4个元素的list，其中第4个元素也是一个list；
  
  执行a.extend(b)结果为包含6个元素的list.

  遍历整个数据集，循环计算熵和splitDataSet函数，找到最好的特征划分方式（信息增益最大的特征）。

#找到信息增益最大的特征
def chooseBestFeaToSplit(dataSet):
    numFeas = len(dataSet[0])-1
    #计算整个数据集的经验熵
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeas = -1
    #遍历数据集中所有特征
    for i in range(numFeas):
        #数据集中第i个特征值写入新的list
        featList = [example[i] for example in dataSet]
        #创建集合，获得唯一属性值
        uniqueVals = set(featList)
        newEntropy = 0.0
        #遍历当前特征中所有唯一的属性值
        for value in uniqueVals:
            #计算当前特征的条件熵
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        #计算信息增益
        infoGain = baseEntropy - newEntropy
        #取得最大信息增益
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeas = i
    return bestFeas

结果返回第0个特征的信息增益最大：

3.构建决策树

由于特征值可能多于两个，第一次划分后数据被传递到树分支的下一个节点，在这个节点上，再次划分数据，采用递归的方式处理数据。
递归结束的条件是：遍历完所有划分数据集的属性，或者每个分支下的所有实例都具有相同的分类，如果所有实例具有相同的分类，则得到一个叶子节点。如果数据集已经处理了所有的属性，但是类标签依然不唯一，通常采用多数表决方法决定叶子节点的分类。

#多数表决
def majorityCnt(classList):
    classCount = {}
    #记录每个类标签出现的频率
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    #排序字典
    sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

通过递归构决策树：

#构造决策树
def createTree(dataSet,labels):
    #数据集所有类标签的列表
    classList = [example[-1] for example in dataSet]
    #所有类标签相同
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    #所有类标签便利完成
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)

    bestFeat = chooseBestFeaToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    #树的信息用字典存储
    myTree = {bestFeatLabel: {}}
    del(labels[bestFeat])

    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    #遍历当前特征值包含的属性值
    for value in uniqueVals:
        #复制类标签存储在新list
        subLabels = labels[:]
        #递归
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

返回嵌套字典：其中第一个关键字’no surfacing’是第一个划分的特征，第二个关键字是’no surfacing’划分的数据集，这些关键字的值为’no surfacing’的子节点，值有可能是类标签，也有可能是一个数据字典。

4. 使用Matplotlib绘制树形图