机器学习分类篇-支持向量机下

前面介绍了线性可分情况下SVM的原理，这里介绍线性不可分下SVM的处理方式。

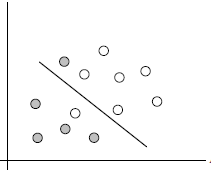
如上图，无论如何不能找到一个超平面将两类点分开，SVM的处理方式主要分两步：
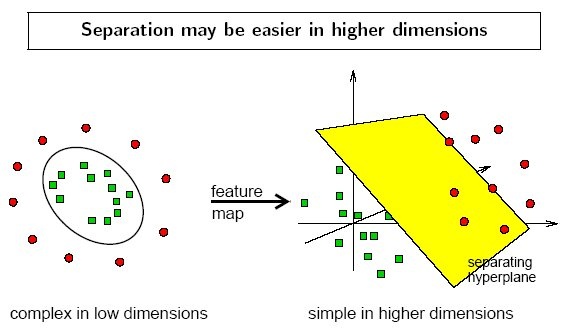
1.利用一个非线性的映射将原数据集转化到高维空间中。
2.在高维空间中找一个超平面根据线性可分的情况处理。

利用上图帮助理解，第一个是典型的2维线性不可分的情况，将其映射到三维空间中分开，就可以按线性可分的情况处理，找一个超平面将其分开。

翻墙后，YouTube的这个演示视频可能更直观一点。
https://www.youtube.com/watch?v=3liCbRZPrZA

那么如何利用非线性映射将数据转化到高维呢？
举个例子：
三维的输入向量 X = (x1, x2, x3)
要转化到六维空间Z中去，可以让
z1 = x1, z2 = x2, z3 = x3, z4 = x1*x2, z5 = x1*x3, z6 = x2*x3
d(Z) = W*Z +b=z1*w1+z2*w2+z3*w3+z4*w4+z5*w5+z6*w6+b

这只是一个例子，我们可以用很多很多方程将低维的数据映射到高维，问题是我们应该如何选择合理的非线性转化将数据转化到高维呢。还有一个问题，从上面我们可以看到计算过程中，大量进行内积运算，运算量非常高，怎么解决这个问题呢。

SVM用核函数(kernel trick)解决这两个问题

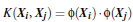
代入核函数运算后的结果是等同于内积运算的结果的，但是运算量远远低于后者。
核函数有很多种，最常用的是高斯径向基核函数RBF

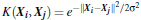
多种核函数的选择可以用经验来判断比如图像分类通常用RBF，文字不用RBF。也可以尝试不同的kernel，根据结果准确度而定。

下面举一个例子来说明核函数的内部原理
假设定义两个向量x = (x1, x2, x3) y = (y1, y2, y3)
定义方程: f(x) = (x1*x1, x1*x2, x1*x3,x2*x1,x2*x2+x2*x3+x3*x1+x3*x2+x3*x3)
将3维向量映射到9维
K(x,y) = (x,y的内积运算)^2

假设x = (1,2,3), y = (4,5,6)
则 f(x) = (1,2,3,2,4,6,3,6,9)
f(y) = (16,20,24,20,25,36,24,30,36)
f(x)和f(y)的内积 = 16+40+72+40+100+180+72+180+324 = 1024

用核函数算呢 K(x, y) = (4 + 10 + 18)^2 = 1024
同样的结果使用kernel方法计算容易很多。