把x1,x2,x3,.....,xn看作常数,而把待定参数θ0,θ2,.....,θn看作 L 的自变量。
对连续型总体X 和 离散型随机变量X,样本的似然函数分别是概率密度 和 分布率的连城形式。
极大似然估计法的基本思想:在OLS估计中,我们假定一个单一总体的参数是确定的。这个总体可以生成大量的随机样本,我们所用的样本不过是其中的一个。总之,在假设的重复抽样过程中会产生大量的样本,因而可以产生总体参数的大量样本估计值。
极大似然估计法(Maximum Likelihood Estimation,MLE)需要对随机扰动项的分布做出假定,通常选择正态分布假定。在极大似然估计中,假定样本是固定的,竹个观测值都是独立观测的,这个样本可由各种不同的总体生成,而每个样本总体都有自己的参数。那么在可供选择的总体中,哪个总体最可能生成所观测到的n个样本值? 为此需要估计每个可能总体取得这n个观测值的联合概率,选择其参数能使观测样本的联合概率最大的那个总体。
最大似然法,在二十世纪二十年代初,由费歇(R,A,Fisher l890—1962)发明的最大似然法(maximum likelihood method)是在所有估计问题中应用范围最广,并且可以从理论上证明由此得到的估计量具有几个理想的特性的方法( 见下面说明)。它可以说是统计估计理论上划时代的发现之一。设总体的概率模型为F(x|θ)。为了说明的方便,暂假定只有一个未知参数,X1,X2,……,Xn是容量为 n 的随机样本(大写X),实际观测到的样本观测值(小写x)为 Xl=x1,X2=x2,……,Xn=xn 。把同各Xi对应的密度函数或概率函数(包括作为未知数的未知参数)的连乘积看成是未知参数的函数,称其为似然函数(Likelihood function)。
也就是说,这样定义的似然函数,就是把手中得到的样本观测值实现的“概率密度或概率”,即“似然程度”看成是未知参数θ的函数。使这一似然程度为最大从而决定θ的值的“方式”,可以说是极为“合理的”估计方式。令作为样本观测值的函数被决定的θ* = g(x1,x2,……,xn)对于一切可能的(先验容许的)θ值,都能满足下列条件
L(θ*)≥L(θ) ①
就是说θ*是使给定的样本观测值的似然程度为最大的θ。这时θ*叫做θ的最大似然估计值。用观测以前的样本(随机变量)X1,X2,……,Xn,代换函数g 的 n 个变量后得到的θ估计值θ^ = g(Xl,X2,……,Xn)叫做根据容量为n的样本计算的最大似然估计量。
如果所有可能的θ的集合是有限集合,要求解满足条件①式的θ值是很容易确定的,然而在大部分的应用问题中,θ的集合是无限集合。因此,在许多场合将似然函数对θ求偏导数,然后需要另外求解的方法。
此外,由于似然函数是非负的,对其进行对数变换是单调递增的变换,所以①式等价于 ㏒ L(θ*)≥㏒ L(θ)
并且, 偏导数㏒/偏导数θ = (1/L) * 偏导数L/偏导数θ
所以使logL(θ)的偏导数为0的θ值 和 使L(θ)的偏导函数为0的θ值相等。
因此,当对L(θ)直接求导比较麻烦时,可以对LogL(θ)求导,从而求得估计值θ^。
似然函数(Likelihood Function):
假定{xi}i=1→n 是从概率密度函数为f(x ; θ)的总体中抽取的独立同分布样本。目标是估计未知参数向量θ∈Rk。
似然函数定义为观察值xi的联合密度L(X;θ),它是θ的函数:
L(x;θ) = ∏f(xi ; θ)
其中,X为样本数据矩阵,由观察值x1 , x2,……,xn组成每一行。
θ的最大似然估计量(maximum likelihood estimator,MLE)定义为θ= arg maxL(X;θ)
通常最大化对数似然函数更容易求
ζ(X;0) = Log L(X;θ)
对数似然函数与似然函数的解是等价的,因为对数转换是单调的一对一映射。即
θ = arg max L(X;θ) = argmaxf(X;θ)
最大化过程总是可以被分析表达的,即我们将得到θ估计值的显式分析表达式。然而不幸的是,在其他一些情形下,最大化过程可能是错综复杂的,牵涉到非线性最优化技术。
给定样本X和似然函数,可将运用数值方法(numerical method)来确定最大化 L(X;θ)或者ζ(X;θ)的θ值,这些数值方法通常是基于牛顿一拉普生(Newton-Raphson)迭代技术。
来自:http://www.zybang.com/question/b404a34559959d22af97c1dc3233c7ce.html
总结:似然函数与概率的区别在于,似然函数引入了参数的概念,是已知概率求参数,概率是已知参数求概率。
举例:
例子:
考虑投掷一枚硬币的实验。通常来说,已知投出的硬币正面朝上和反面朝上的概率各自是pH = 0.5,便可以知道投掷若干次后出现各种结果的可能性。比如说,投两次都是正面朝上的概率是0.25。用条件概率表示,就是:
其中H表示正面朝上。
在统计学中,我们关心的是在已知一系列投掷的结果时,关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型:假设硬币投出时会有pH 的概率正面朝上,而有1 − pH 的概率反面朝上。这时,条件概率可以改写成似然函数:
也就是说,对于取定的似然函数,在观测到两次投掷都是正面朝上时,pH = 0.5 的似然性是0.25(这并不表示当观测到两次正面朝上时pH = 0.5 的概率是0.25)。
如果考虑pH = 0.6,那么似然函数的值也会改变。
注意到似然函数的值变大了。这说明,如果参数pH 的取值变成0.6的话,结果观测到连续两次正面朝上的概率要比假设pH = 0.5时更大。也就是说,参数pH 取成0.6 要比取成0.5 更有说服力,更为“合理”。总之,似然函数的重要性不是它的具体取值,而是当参数变化时函数到底变小还是变大。对同一个似然函数,如果存在一个参数值,使得它的函数值达到最大的话,那么这个值就是最为“合理”的参数值。
在这个例子中,似然函数实际上等于:
-
 , 其中
, 其中
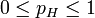 。
。
如果取pH = 1,那么似然函数达到最大值1。也就是说,当连续观测到两次正面朝上时,假设硬币投掷时正面朝上的概率为1是最合理的。
类似地,如果观测到的是三次投掷硬币,头两次正面朝上,第三次反面朝上,那么似然函数将会是:
-
 , 其中
T表示反面朝上,
, 其中
T表示反面朝上,
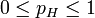 。
。
这时候,似然函数的最大值将会在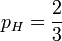 的时候取到。也就是说,当观测到三次投掷中前两次正面朝上而后一次反面朝上时,估计硬币投掷时正面朝上的概率
的时候取到。也就是说,当观测到三次投掷中前两次正面朝上而后一次反面朝上时,估计硬币投掷时正面朝上的概率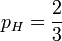 是最合理的。
是最合理的。








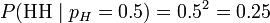
















 1533
1533

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








