概率模型有时既含有观测变量(observable variable),又含有隐变量(latent variable)。如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计或贝叶斯估计来计算模型参数。但是,当模型含有隐变量时,就不能简单地使用以上估计方法,而EM算法就是针对含有隐变量的概率模型参数的极大似然估计法。
一般地,用 X 表示可观测随机变量的数据,
Z
表示隐随机变量的数据, X 和
Z
连在一起称为完全数据(complete-data),观测数据 X 又称为不完全数据(incomplete-data)。假设给定观测数据
X
,其概率分布是 P(X|θ) ,其中 θ 是需要估计的模型参数,那么不完全数据 X 的似然函数是
P(X|θ)
,对数似然函数 L(θ)=logP(X|θ) ;假设 X 和
Z
的联合概率分布是 P(X,Z|θ) ,那么完全数据的对数似然函数是 logP(X,Z|θ) 。对于不完全数据的统计估计问题,EM算法已经成为了一种通用的工具。
从掷硬币实验说起
给定两枚硬币 A 和
B
,它们出现正面的概率分别为 θA 和 θB (未知),我们的目标是通过重复5次以下实验来估计 θ=(θA,θB) 。
选择一枚硬币,并且知道具体是哪一枚,然后用选中的硬币掷十次,记录结果。因此,总共进行了50次掷硬币的实验。如下图所示
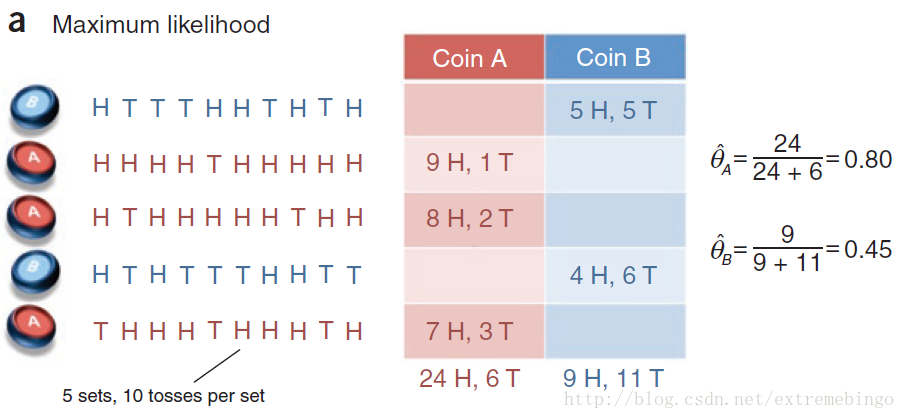
现在,引入两个随机变量 X={
X1,X2,X3,X4,X5} 和 Z={
Z1,Z2,Z3,Z4,Z5} ,其中 Xi∈{
0,1,⋯,10} 表示第 i 次实验硬币正面朝上的次数,
Zi∈{A,B}
表示第 i 次实验所用的硬币。上述问题为完全数据的参数估计问题,可通过正面出现的比例进行估计
θA^=# of heads using coin Atotal # of flips using coin AθB^=# of heads using coin Btotal # of flips using coin B
事实上,上述的估计方式就是统计学上的最大似然估计。
现在考虑一个更有挑战性的参数估计问题。只给定硬币出现正面的次数,而不给定是由哪一枚硬币掷出的,即 Z 为隐含变量。因此,该问题就转化为不完全数据的参数估计问题。此时,由于不知道具体是哪一枚硬币,所以无法通过直接计算硬币出现正面的次数来估计
θ
。当概率模型存在隐变量时,不能简单地使用极大似然估计,需要采用下文的EM算法来计算模型参数。
凸函数
定义1 定义在区间 I=[a,b] 上的实函数 f ,如果对于
∀x1,x2∈I,λ∈[0,1]
,函数 f 满足以下不等式
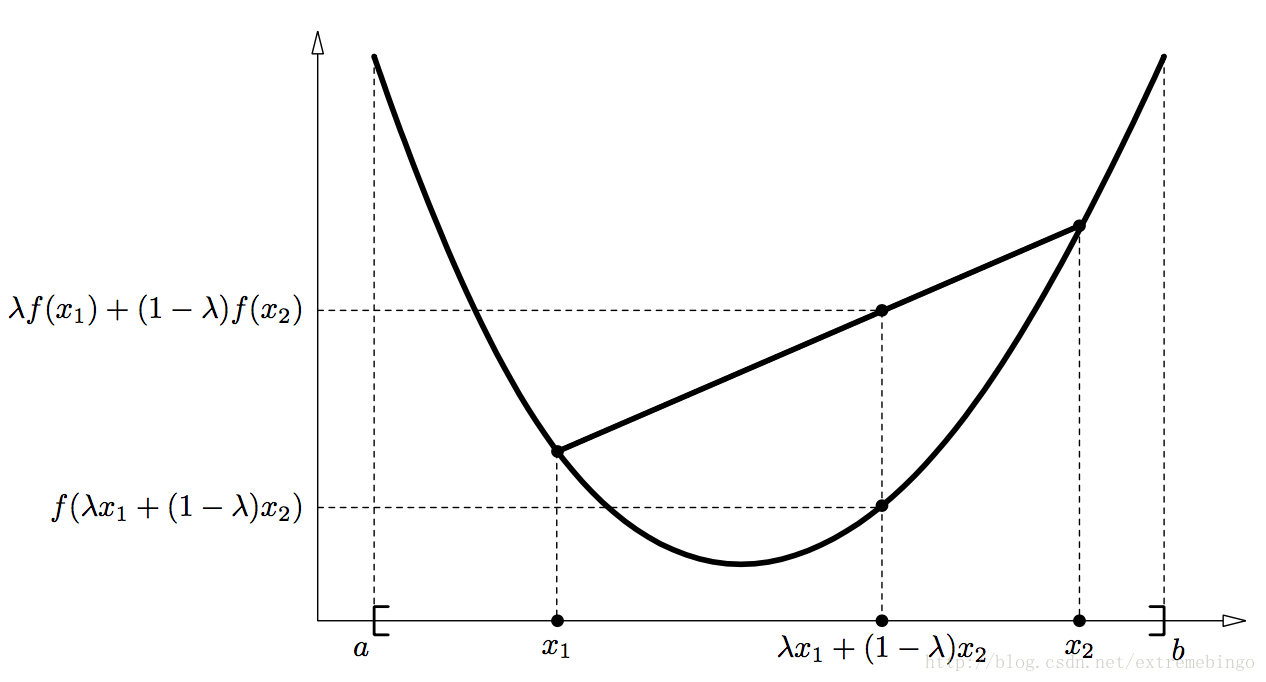
f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2)(1)
则称函数 f 为凸函数。其几何解释如下图所示
定义2 如果函数
−f
是凸函数,则函数 f 是凹函数。
定理1 如果函数
f
在区间 [a,b] 上二阶可导,并且 f′′(x)≥0 ,则 f 在区间
[a,b]
上为凸函数。
定理2(Jensen inequality) f 为区间
[a,b]
上的凸函数,若 x1,x2,⋯,xn∈I ,并且 λ1,λ2,⋯,λn≥0,∑ni=1=1 ,则以下不等式成立
f(∑i=1nλixi)≤∑i=1nλif(xi)(2)
证明: 使用数学归纳法证明
- 当 n=1 时,(2)式显然成立,并取得等号。
- 当 n=2 时,即为凸函数的定义。
- 假设当 n=n 时(2)式成立,则
f(∑i=1n+1λixi)=f(λn+1xn+1+∑i=1nλixi)=f(λn+1xn+1+(1−λn+1)11−λ








 EM算法是一种处理含有隐变量概率模型参数估计的方法。通过掷硬币实验介绍问题背景,深入讲解EM算法的E-step和M-step,以及在高斯混合模型中的应用。涉及凸函数概念,Jensen不等式,并讨论算法的收敛性和初值选择的重要性。
EM算法是一种处理含有隐变量概率模型参数估计的方法。通过掷硬币实验介绍问题背景,深入讲解EM算法的E-step和M-step,以及在高斯混合模型中的应用。涉及凸函数概念,Jensen不等式,并讨论算法的收敛性和初值选择的重要性。


 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








