量化投资投资学基础

飓风神龙

已于 2024-10-31 16:39:16 修改

阅读量824

点赞数 14

文章标签：量化交易金融 python 学习

于 2024-10-20 00:25:53 首次发布

本文链接：https://blog.csdn.net/fan1102958151/article/details/143029626

版权

投资

什么是投资

投资是为了获得可能但并不确定的未来值（Future value）而作出牺牲确定的现值（Present value）的行为。（William F.Sharpe，1990年获得诺贝尔经济学奖）

投资有三大特点

投资的时间性：资金具有时间价值，是牺牲当前消费（Reduced current consumption）和计划未来消费（Planned later consumption）之间的权衡
投资的不确定性（Uncertainty）：也即风险性，如果证券没有风险是否意味着没有收益？
投资的收益性：增加投资者的财富来满足未来的消费

什么是投资学

投资学（Investments)是研究投资行为及均衡定价的科学，又分为微观金融学(finance) 和宏观金融学(macro-finance) 以及交叉学科。

微观金融学包括公司金融、投资学、证券市场微观结构。
宏观金融学包括货币银行学、国际收支理论、金融体系稳定性研究、微观金融学的自然延伸。
交叉学科又包含Financial Engineering和Law and Finance。

投资学主要内容

金融资产

实物资产：取决于该社会经济的生产能力，为经济创造净利润，如土地、建筑物、机器以及可用于生产产品和提供服务的知识。金融资产：对实物资产的索取权

金融资产主要分为四大类：

固定收益型或债务型证券
普通股或权益型证券
基金
衍生产品（期货、期权、互换）

主要市场

主要的市场主要分为债券市场、外汇市场、贵金属市场、大宗商品市场和股票市场

债卷市场

债券市场有以下几个特点：

120万亿规模大，场内场外将互通
利率债和信用债
到期收益率是重要指标，可以参考国债期货
用EXCEL表计算到期收益率
投资方法：被动投资和积极投资

债券价格的六大原理：

债券价格与市场利率变化成反比。
债券价格受利率变动的影响大小，与初始市场利率的高低成反比（低利率时期，市场利率变动对债券价格变动造成更大影响）
长期债券的价格受市场利率的影响大于短期债券。
债券价格受市场利率影响的程度随到期期限的延长而递减。
债息率越低债券受市场利率变化的影响越大。
市场利率下降使债券价格上涨的幅度，大于市场利率上升使债券价格下降的幅度。

债券的到期收益率计算方式：到期收益率是债券价格的逆运算，是债券的支付现值与其价格相等的折现率。到期收益率通常被视为在购买日至到期日之间持有债券所获得平均收益率的测量。

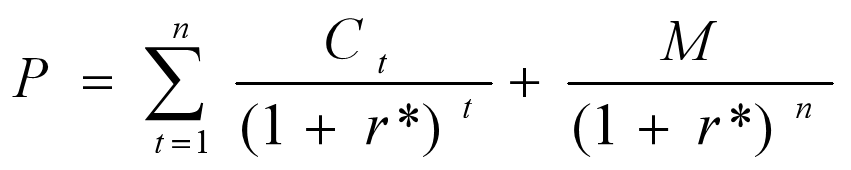
三个条件：持有到期；再投资收益率等于到期收益率；发行人按期支付利息。

外汇市场

美元指数
人民币汇率
避险货币
商品货币
数字货币

贵金属市场

黄金和白银
与美元指数有关
避险功能
与通胀相关
与大宗商品有色金属关联
与风险资产负相关

大宗商品市场

石油
有色金属
黑色系
化工
农产品
软商品

股票市场

在股票市场中，举例：2021年A股呈现以下特点：

高波动性：A股市场一直以来都有较高的波动性，价格会受到各种因素的影响，包括经济数据、政策变化、市场情绪等。投资者需要注意市场风险，并做好风险管理。
相对较高的估值：与一些发达市场相比，A股市场的估值水平可能相对较高。这可能是因为中国经济增长潜力被看好，以及境内外资金流入的影响。
行业结构的调整：中国政府一直在推动经济结构的转型升级，这也影响了A股市场的行业结构。一些新兴行业，比如新能源、消费升级、科技创新等，可能受到更多市场关注。
政策影响：政策对A股市场有很大影响力，一些政策调整可能会对市场产生正面或负面的影响。投资者需要及时关注政策动向，并据此进行投资决策。

金融市场与经济

金融市场的信息作用: 促使资本流向前景良好的公司
消费时机: 通过购买金融资产来储存财富，将来卖出这些金融资产以供消费。
风险分配: 投资者可以选择满足自身特定风险偏好的证券。
所有权和经营权的分离: 获得稳定性的同时也引发了代理问题。

投资过程

资产配置：对资产大类的选择
证券选择：在每一资产大类中选择特定的证券，证券分析包括对证券进行估价和决定使投资组合集中在那些最具吸引力的资产上。

市场参与者

公司 – 净借款者
家庭 – 净储蓄者
政府 – 既可能是借款者又可能是储蓄者
金融中介：集中资金进行投资。包含：投资公司（公募、私募、财务公司）、商业银行、保险公司
投资银行
风险投资与私募股权

基础数理概念

概述

在概率论的建模中，我们往往假设随机变量的分布已知，但是这个假设在实际中时很难做到的。

统计学能做的就是找到最佳的参数，如正态分布的 $\mu$ 和 $\delta ^2$ ，也会关心 $\mu$ 和 $\delta ^2$ 是否符合符合相关要求。

使用一个更通俗的例子来说，由于概率论的建模，现在假设中国人的身高近似服从正态分布，那究竟这个正态分布中的 $\mu$ 和 $\delta ^2$ 的值是多少就是统计学做的事情，而这个工作也叫做参数估计。

一般认为，统计学是收集、分析、表述和解释数据的科学，统计学是一门处理数据的方法和技术的学科。

《概率论》学习笔记

概率论与统计学的关系

基本概念

总体：研究对象的全体，它是一个随机变量，用XX表示。

个体：组成总体的每个基本元素。

简单随机样本：来自总体XX的nn个相互独立且与总体同分布的随机变量X1,X2⋯ ,XnX1,X2⋯,Xn，称为容量为nn的简单随机样本，简称样本。

统计量：设X1,X2⋯ ,Xn,X1,X2⋯,Xn,是来自总体XX的一个样本，g(X1,X2⋯ ,Xn)g(X1,X2⋯,Xn)）是样本的连续函数，且g()g()中不含任何未知参数，则称g(X1,X2⋯ ,Xn)g(X1,X2⋯,Xn)为统计量。

样本均值： X‾=1n∑i=1nXiX=n1∑i=1nXi 样本方差：S2=1n−1∑i=1n(Xi−X‾)2S2=n−11∑i=1n(Xi−X)2

样本矩：样本kk阶原点矩：Ak=1n∑i=1nXik,k=1,2,⋯Ak=n1∑i=1nXik,k=1,2,⋯

样本kk阶中心矩：Bk=1n∑i=1n(Xi−X‾)k,k=1,2,⋯Bk=n1∑i=1n(Xi−X)k,k=1,2,⋯

分布

χ2χ2分布：χ2=X12+X22+⋯+Xn2∼χ2(n)χ2=X12+X22+⋯+Xn2∼χ2(n)，其中X1,X2⋯ ,Xn,X1,X2⋯,Xn,相互独立，且同服从N(0,1)N(0,1)

tt分布：T=XY/n∼t(n)T=Y/nX∼t(n) ，其中X∼N(0,1),Y∼χ2(n),X∼N(0,1),Y∼χ2(n),且XX，YY 相互独立。

FF分布：F=X/n1Y/n2∼F(n1,n2)F=Y/n2X/n1∼F(n1,n2)，其中X∼χ2(n1),Y∼χ2(n2),X∼χ2(n1),Y∼χ2(n2),且XX，YY相互独立。

分位数：若P(X≤xα)=α,P(X≤xα)=α,则称xαxα为XX的αα分位数

正态总体的常用样本分布

设X1,X2⋯ ,XnX1,X2⋯,Xn为来自正态总体N(μ,σ2)N(μ,σ2)的样本，X‾=1n∑i=1nXi,S2=1n−1∑i=1n(Xi−X‾)2,X=n1∑i=1nXi,S2=n−11∑i=1n(Xi−X)2,则：

(1) X‾∼N(μ,σ2n) X∼N(μ,nσ2) 或者X‾−μσn∼N(0,1)nσX−μ∼N(0,1)

(2) (n−1)S2σ2=1σ2∑i=1n(Xi−X‾)2∼χ2(n−1)σ2(n−1)S2=σ21∑i=1n(Xi−X)2∼χ2(n−1)

(3) 1σ2∑i=1n(Xi−μ)2∼χ2(n)σ21∑i=1n(Xi−μ)2∼χ2(n)

(4) X‾−μS/n∼t(n−1) S/nX−μ∼t(n−1)

重要公式与结论

(1) 对于χ2∼χ2(n)χ2∼χ2(n)，有E(χ2(n))=n,D(χ2(n))=2n;E(χ2(n))=n,D(χ2(n))=2n;

(2) 对于T∼t(n)T∼t(n)，有E(T)=0,D(T)=nn−2(n>2)E(T)=0,D(T)=n−2n(n>2)；

(3) 对于F ~F(m,n)F ~F(m,n)，有 1F∼F(n,m),Fa/2(m,n)=1F1−a/2(n,m);F1∼F(n,m),Fa/2(m,n)=F1−a/2(n,m)1;

(4) 对于任意总体XX，有 E(X‾)=E(X),E(S2)=D(X),D(X‾)=D(X)nE(X)=E(X),E(S2)=D(X),D(X)=nD(X)