1.11 数字信号

1.11 数字信号

1.11 数字信号

我们已经讨论了通过对时间轴进行采样来获得离散时间信号，并通过对频率轴进行采样来获得离散频率集合。相同的概念可以应用于幅度轴，在幅度轴上，信号幅度可以被采样为仅包含有限集合的离散值。这样的离散时间、离散值的信号称为数字信号，与之相对的是模拟信号，后者在时间上和幅度上都是连续的。

​​

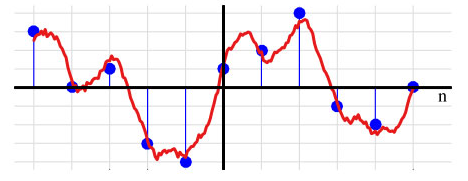
图1.73：通过对y轴切片来获得数字信号

图1.73显示了如何通过对底层连续幅度进行切片来获得具有固定值集合的数字信号。例如，幅度为2.2的信号可以被舍入为2、1.4或1，依赖于所需的分辨率。

计算机只能处理数字信号，因为离散时间信号虽然仅定义在有限的时间值上——但在幅度轴上可以有无限值。正如计算机内存是有限的并且只能存储已知数量的时间值，其宽度也是有限的（例如，8位），并且只能存储有限数量的幅度值（例如，对于一个8位宽的内存，我们可以有 $2^8=256$ 个幅度值）。

1.12 小画面

英语中有26个字母，并且有许多规则将它们连接成单词。参照图1.55，基本DSP的语言要简单得多。

1. 只有一个字母：时间为0的采样（可以被任意数缩放）。该采样的DFT是频域中的频率为0的单个序列，实际上是具有频率为0的复数正弦波。
2. 只有一个主要规则：该采样中的时间移位 $n_0$ 生成了一个相移，实际上在频域中是具有倒数周期 $n_0$ 的复数正弦波。

任何离散时间序列都可以被视为移位并缩放的采样和的总和。

第二章、系统

一个执行某些规定操作以在输入信号上生成输出信号的设备或算法被称为系统。如图2.1所示，通过无线介质从点A到点B的通信是由三个系统组成的游戏：

​​

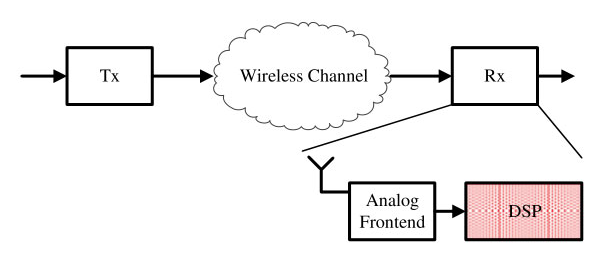
图2.1：无线通信是由3个系统组成的

• Tx：Tx系统生成要通过空气或任何其他介质传输的信号。
• 无线信道：尽管无线信道可能看起来像敌人，但它是承载Tx信号到达Rx的系统。通过广泛的测量实验，科学家已经对该信道进行了相当深入的研究。因此，Tx和Rx的传输策略基于以最优方式应对无线信道所带来的障碍。
• Rx：理想情况下，Rx应该执行与Tx执行操作的精确逆向操作。然而，由于无线信道在信号传递过程中引入了弱且失真的信号，Rx系统的任务变得更加艰巨，并且包含了若干额外的操作。通过子系统高效解决这些问题是通信的核心。图2.1中展示了两个子系统，分别是一个调节输入信号以准备进行数字处理的模拟前端和一个应用高效算法以恢复Tx数据的数字信号处理（DSP）引擎。这就是软件定义无线电（SDR）。

2.1 线性系统

一个线性系统意味着，如果两个输入被缩放并相加在一起形成一个新的输入，那么系统的新输出也是它们各自输出的缩放和。

缩放（Scaling）：

对于缩放成立，如果

输入 $s_1[n]$ 产生输出 $r_1[n]$

那么

输入 $\alpha s_1[n]$ 产生输出 $\alpha r_1[n]$

其中，$\alpha$ 是任意标量。

相加（Addition）：

当两个这样的输入相加在一起时，输出应该是它们各自输出的和，如

输入 $s_1[n]+s_2[n]$ 产生输出 $r_1[n]+r_2[n]$

一个线性系统将上述两个特性结合起来，即缩放和相加，如

输入 ${\alpha }_1{s}_1[n]+{\alpha }_2{s}_2[n]$ 产生输出 ${\alpha }_1{r}_1[n]+{\alpha }_2{r}_2[n]$ （公式 2.1）

下面，我们讨论线性系统和非线性系统的例子。

---

例 2.1

考虑一个系统

$$r[n] = \frac{3}{7} \cdot s[n]$$

该系统的输出，响应于输入 $1\cdot s_1[n]=1\cdot \sin (2\pi 0.1n)$，是

$$r_1[n] = \frac{3}{7} \sin(2\pi 0.1n)$$

类似地，它对另一个不同信号 $2\cdot s_2[n]=2\cdot \sin (2\pi 0.3n)$ 的响应是

$$r_2[n] = \frac{3}{7} (2) \sin(2\pi 0.3n) = \frac{6}{7} \sin(2\pi 0.3n)$$

当该系统接收到输入 $1\cdot s_1[n]+2\cdot s_2[n]$ 时，输出是

$$r[n] = \frac{3}{7} \left( 1 \cdot \sin(2\pi 0.1n) + 2 \cdot \sin(2\pi 0.3n) \right) = \frac{3}{7} \sin(2\pi 0.1n) + \frac{6}{7} \sin(2\pi 0.3n) = r_1[n] + r_2[n]$$

因此，它是一个线性系统。

另一方面，当相同的输入 $1\cdot s_1[n]+2\cdot s_2[n]$ 被给予另一个系统时

$$r[n] = s^2[n]$$

使用恒等式 sin ⁡ ( A ) sin ⁡ ( B ) = 0.5 { cos ⁡ ( A − B ) − cos ⁡ ( A + B ) } \sin(A) \sin(B) = 0.5 \{ \cos(A-B) - \cos(A+B) \} sin(A)sin(B)=0.5{cos(A−B)−cos(A+B)}，输出是：

$$r[n] = \left( 1 \cdot \sin(2\pi 0.1n) + 2 \cdot \sin(2\pi 0.3n) \right)^2 \\= \sin^2(2\pi 0.1n) + 4 \cdot \sin^2(2\pi 0.3n) + 4 \cdot \sin(2\pi 0.1n) \sin(2\pi 0.3n) \\= \sin^2(2\pi 0.1n) + 4 \cdot \sin^2(2\pi 0.3n) + 2 \cdot \cos(2\pi 0.2n) - 2 \cdot \cos(2\pi 0.4n) \\\neq r_1[n] + r_2[n] \\= \sin^2(2\pi 0.1n) + 4 \cdot \sin^2(2\pi 0.3n)$$

显然，这是一个非线性系统。

我们可以从上面的例子中推导出，如果在地面上绘制 $x$ 轴和 $y$ 轴作为独立变量，那么图2.2中加沙大金字塔和悉尼歌剧院的轨迹可以分别与线性系统和非线性系统相关联。

‍

​​

图2.2：加沙大金字塔和悉尼歌剧院