Stanford Machine Learning 公开课笔记(3) Neural Network

最近在Coursera上学习Stanford的Andrew Ng的Machine Learning公开课，也做笔记，写作业。本章是Neural Network, 记录一下我的笔记。大部分是课堂视频截图，形式比较丑。写完编程作业(主要用octave来实现，和matlab语法很像)之后，发现写作业并且在系统中提交通过才能给你带来真正地学会了的感觉，推荐认真听课并且独立完成作业。

同样，首先记录自己的几个疑问

1 如何决定神经网络有多少层？
2 Gradient的为什么可以按照课件中讲解的方式进行计算?
3 神经网络和逻辑回归什么关系?

Why do we Need Neural Networks?
because we sometimes need to learn complex machine learning hypothesis.如下图
假设有一个2元分类问题，只有2个特征X₁和X₂，打算用逻辑回归来学习，由于目测decision boundary非常扭曲，所以构造X₁和X₂的所有的Polynomial  terms作为逻辑回归的特征参与训练。这样可以最大限度地得到一个很好的分类器。
假设有5000+个feature,那么构造出来的这样构造出来的Polynomial将会非常复杂。如果假定Polynomial的最高次为a，那么将会有O(N的a次方)个可能性。
这说明，logistic regression and linear regression are not suitable for complex non-linear hypothesis.
所以应该用新方法，也就是神经网络的方法，来解决非线性的问题。 

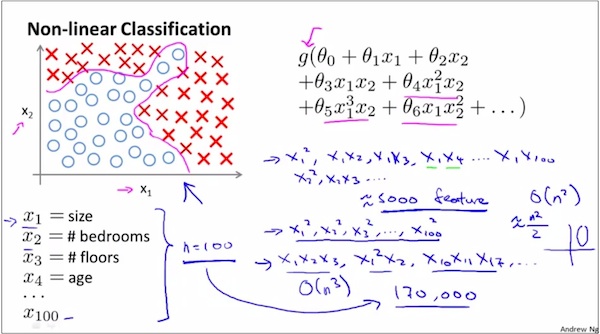
如下，假设有2500个像素，那么二次特征将有(1+2500)*2500/2≈3million

Neural network model representation-1
The leftmost is the input layer, the rightmost layer is the output layer. the rest are the hidden layers.

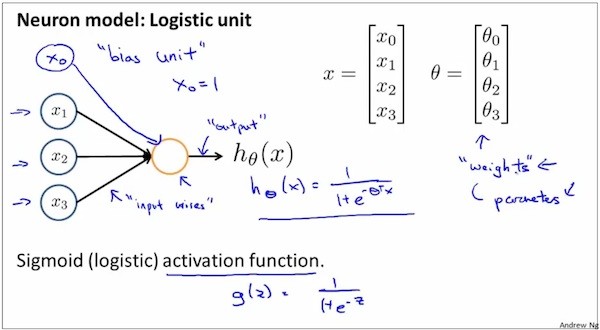
Neural network model representation-2

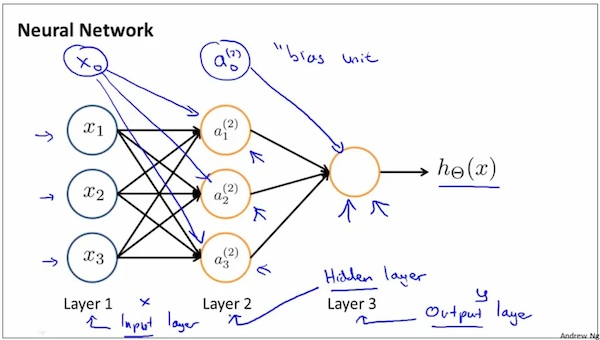
Neural network model representation-3
可以这样来理解θ(j)矩阵。把它看成layer j经过矩阵乘法变化到了layer j+1，即θ * layer (j) = layer (j+1), 所以维度如下。

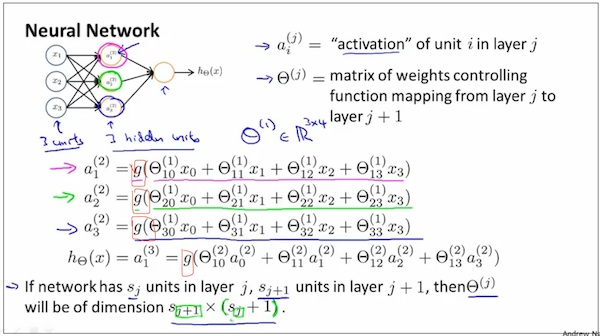
How can neural network handle complex non-linear questions?   Intuition1
下面的分类问题是个是XOR问题，它的decision boundary是非线性的。

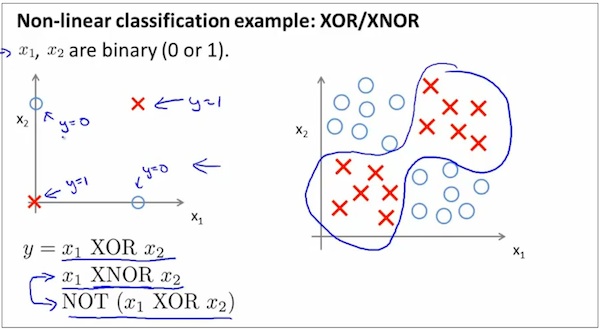
下面采用神经网络方法来求解XOR问题，step1

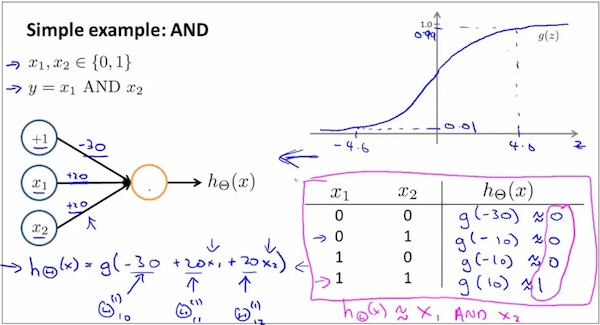
下面采用神经网络方法来求解XOR问题，step2

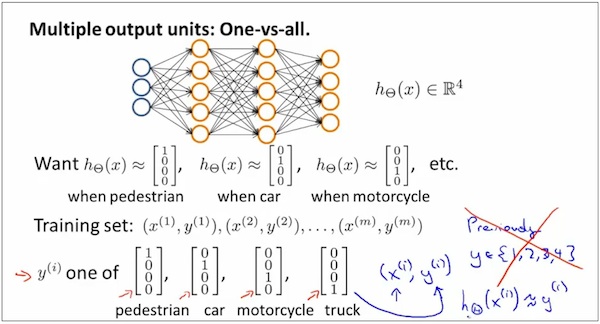
扩展 multi-class neural network
类似逻辑回归的one-vs-all方法

Neural Network Cost Function

在regularization部分，Neural Network的regularization部分并不计算bias unit的θ值。类似的，Logistic Regression的regularization部分也不计算bias unit的theta值。

如何求Neural Network问题的Gradient
1. 先理解什么叫做Gradient。类比之前的模型。
对于线性回归，Gradient是θ的偏导数，θ₀，θ₁，θ₂是标量，Gradient可用于使用Gradient Descent方法去求解Cost Function的最小值
对于逻辑回归，Gradient是θ的偏导数，θ₀，θ₁，θ₂是标量，Gradient可用于使用Gradient Descent方法去求解Cost Function的最小值
对于神经网络，Gradient是θ的偏导数，θ₀，θ₁，θ₂是二维的矩阵(这是因为神经网络的θ本来就是二维的矩阵，这在Forward 
Propagation和 Backward Propagation中能够明显地看出来，所以得到的Gradient也是二维的矩阵了)，同样，Gradient可用于使用Gradient Descent方法去求解Cost Function的最小值。

2. 简化问题，假设输入只有一份，用这一份输入进行训练。

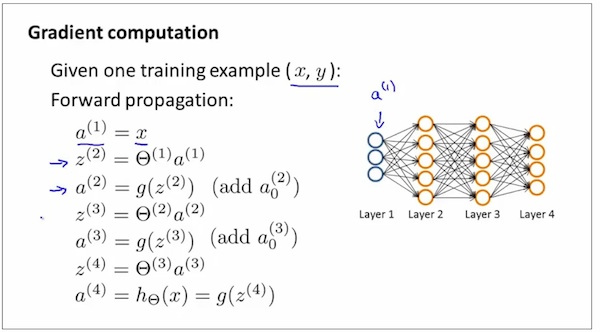
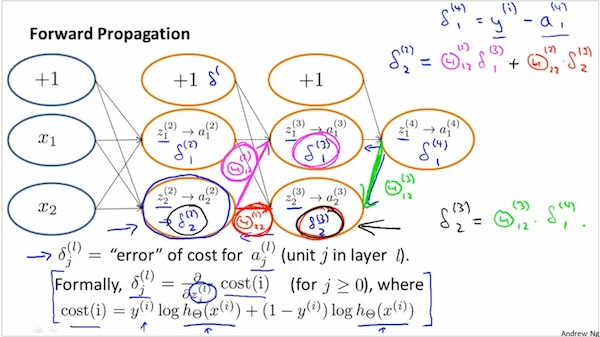
在下图中，分别计算layer 2 ~ layer l 的误差δ。 注意 1 没有计算δ¹，因为layer1是输入，没有误差。
注意 2 g’的展开表达式省略了严格证明，如图手写所示，暂时不证明为什么展开式这样。
注意 3 可以通过复杂的数学证明得出，下面的δ和gradient是相关的

gradient的具体计算方法

如何理解gradient的计算式呢？
先简化问题

如下图，δ是cost(i)对z的偏导数。z是中间变量，是sigmoid(z)中的z。
What these delta terms are？they turn out to be the partial derivative of the cost function with respect to these intermediate terms that we're computing.
And so their measure of how much would we like to change the neural network's weights in order to  affect these intermediate values of the computation,
so as to affect the final output the neural network h of x and therefore affect the overall cost.

Octave中使用Neural Network的注意事项1
如何在octave中对Neural Network进行计算呢 重点是unroll parameters
step1

上图中的D代表 gradient matrices.

Octave中使用Neural Network的注意事项2
使用Gradient Checking进行验证
在迭代计算过程中，即使cost function在下降，依然可能把gradient算错了。
Gradient checking 1

Gradient checking 2

Gradient checking 3

Gradient checking 4

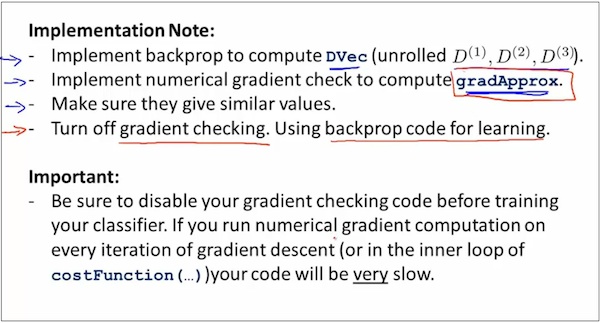
记住，在复杂模型中，不要忘记使用Gradient Checking来验证是否计算争取了。另外，验证之后，在训练阶段，要关闭验证过程，否则训练将会非常缓慢。

Octave中使用Neural Network的注意事项3
Random Initialization
为什么需要random initialization?

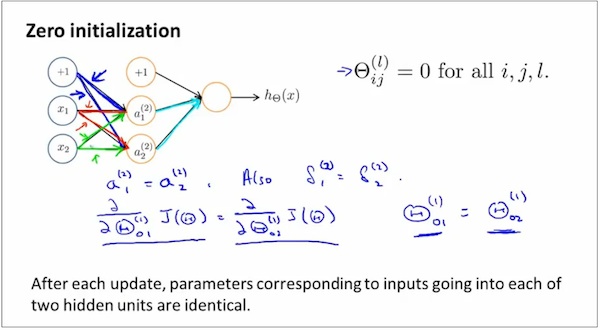
如何进行random initialization

Octave中使用Neural Network的注意事项4
多少层hidden layer?
The more hidden unit, the better, but to many hidden units might be computationally expensive.

Training的过程步骤

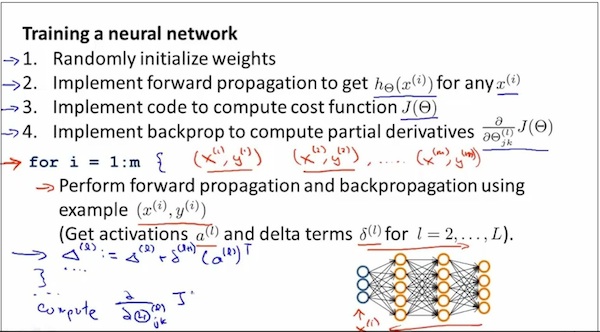
注意1 虽然神经网络的J(θ)不是凸函数，虽然不能理论上保证达到global mimimun，但是用神经网络得到的local mimimun结果也是很好的，在实际中往往表现很好。
注意2 What back propagation is doing is computing the direction of the gradient, and what gradient descent is doing is it's taking little steps downhill until hopefully it gets to。

现在回答开头的问题

1 如何决定神经网络有多少层？

   理论上说，层数越多，效果越好，但是开销也会越高。实际用途中，一般选择使用hidden layer1~2层。
2 Gradient的为什么可以按照课件中讲解的方式进行计算?
   直接使用对矩阵求导的数学公式。

3 神经网络和逻辑回归什么关系?

   可以认为神经网络把逻辑回归进行了很多层，每一层的输出都是下一层的输入。