MATLAB实现光波导的仿真

最新推荐文章于 2023-05-31 09:30:30 发布

matlab练习生

最新推荐文章于 2023-05-31 09:30:30 发布

阅读量2k

点赞数 5

分类专栏： # MATLAB光学建模仿真文章标签：算法 matlab 开发语言

本文链接：https://blog.csdn.net/fendoudecheng/article/details/130404642

版权

MATLAB光学建模仿真专栏收录该内容

25 篇文章 88 订阅

订阅专栏

波导中，以平板介质光波导为例，TE模是电矢量平行于界面的导波

从射线光学入手，这里的光按照是不是在侧壁上实现全反射，分为导行波和辐射波

结合光的反射、折射的相关概念，当入射角大于临界角时，可以实现全反射。

在波导中传播时，光的相位变化包括两部分：沿光路传播导致的光程差，以及在反射面上产生的相位差。

对于s光和p光（电矢量分别垂直和平行于入射面），对应的反射产生的相位差不同：

$\phi_s=-2\arctan{\frac{\sqrt{\beta^2-n_2^2k^2}}{\sqrt{n_1^2k^2-\beta^2}}}$

$\phi_p=-2\arctan{\frac{n_1^2\sqrt{\beta^2-n_2^2k^2}}{n_2^2\sqrt{n_1^2k^2-\beta^2}}}$

其中：

$\beta=n_1k\cos{\theta_1}$

如此，可以表示出TE模在宽度为d的光波导内传播的特征方程：

$\tan{\left(\kappa d\right)}=\frac{\kappa\left(\gamma+\delta\right)}{\kappa^2-\gamma\delta}$

其中：

$\kappa=n_1k\sin{\theta_1}$

$\gamma=\sqrt{\beta^2-n_2^2k^2}=\sqrt{\left(n_1^2-n_2^2\right)k^2-\kappa^2}$

$\delta=\sqrt{\beta^2-n_3^2k^2}=\sqrt{\left(n_1^2-n_3^2\right)k^2-\kappa^2}$

同时，TM模的特征方程也可以表示出来：

$\tan{\left(\kappa d\right)}=\frac{n_1^2\kappa\left(n_3^2\gamma+n_2^2\delta\right)}{n_2^2n_3^2\kappa^2-n_1^4r\delta}$

可以看到这样的特征不能得到简单的解析解，用作图和数值求解可以进行求解。

用作图法求解时，对应的方程如下所示：

$\tan{\left(x\right)}=F\left(x\right)=\frac{x\left[\sqrt{V_{12}^2-x^2}+\sqrt{V_{13}^2-x^2}\right]}{x^2-\sqrt{V_{12}^2-x^2}\sqrt{V_{13}^2-x^2}}$

程序如下：

clear
close all
n1 = 1.56; %芯层折射率
n2 = 1.2;
n3 = 1;
d = 3e-6;
lambda = 1.55e-6;
k = 2*pi/lambda;

V12 = sqrt(n1^2-n2^2)*k*d;
V13 = sqrt(n1^2-n3^2)*k*d;

F = @(x) (x*(sqrt(V12^2-x^2)+sqrt(V13^2-x^2))./(x^2-(sqrt(V12^2-x^2)*sqrt(V13^2-x^2))));

ezplot(@tan,[0,4*pi,-5,5])
hold on
ezplot(F,[0,4*pi])
title('Graphical solution of the eigenvalue')
xlabel('\kappa d')

结果：

从图中可以大致观察到方程解的位置。这里估计第一个解为：x = 2.727

x = 2.727;

用得到的解反计算出光波导中的模式：

kappa = x/d;
theta = asin(kappa/(n1*k));
beta = (n1*k)*cos(theta);
 
disp(['    x = ',num2str(x)]);
disp(['kappa = ',num2str(kappa)]);
disp(['theta = ',num2str(theta)]);
disp([' beta = ',num2str(beta)]);

可以得出相应的结果。

对应的，我们可以使用数值求解的方式更方便的得到结果：

Feigin = @(x) (F(x)-tan(x));

x(1) = fzero(Feigin,3);
x(2) = fzero(Feigin,6);
x(3) = fzero(Feigin,8.5);
x(4) = fzero(Feigin,10.6);

kappa = x/d;
theta = asin(kappa/(n1*k));
beta = (n1*k)*cos(theta);
gamma = sqrt((n1^2-n2^2)*k^2-kappa.^2);
delta = sqrt((n1^2-n3^2)*k^2-kappa.^2);

format short g
A = [x' theta' beta' kappa' gamma' delta'] %数据显示

此时，A的每一列分别存储了对应的解。

需要注意的是，这种数值求解的方法，实际上还是需要大致知道解的位置的。

对于TM模式，上述解法仍然成立。

得到解后，我们要讨论解的有效性，概括来说就是有意义的解对应的有物理意义的值应当是实数。

也就是需要满足：

$\kappa d=x\le V_{12}$

就像讨论方程根是否存在，我们讨论是否一定存在一个模式，能在波导中稳定传播。

满足条件的模式应当是上述特征方程的实数解。

在对称的平面光波导中，这样的模式一定存在，叫做基模，但在非对称光波导中，不一定。

可以绘制图像来说明这一点：

V12 = 0.7;
V13 = 1.1;
F = @(x) (x*(sqrt(V12^2-x^2)+sqrt(V13^2-x^2))./(x^2-(sqrt(V12^2-x^2)*sqrt(V13^2-x^2))));

figure(1)
subplot(1,2,1)
ezplot(@tan,[0,1.5*pi,-5,5])
hold on 
ezplot(F,[0,1.5*pi,-5,5])
title(['Graphical solution of the eigenvalue: V_{12}=',num2str(V12),',V_{13}=',num2str(V13)])
xlabel('\kappa d')

V13 = 0.7;
F = @(x) (x*(sqrt(V12^2-x^2)+sqrt(V13^2-x^2))./(x^2-(sqrt(V12^2-x^2)*sqrt(V13^2-x^2))));

subplot(1,2,2)
ezplot(@tan,[0,1.5*pi,-5,5])
hold on 
ezplot(F,[0,1.5*pi,-5,5])
title(['Graphical solution of the eigenvalue: V_{12}=',num2str(V12),',V_{13}=',num2str(V13)])
xlabel('\kappa d')

结果：

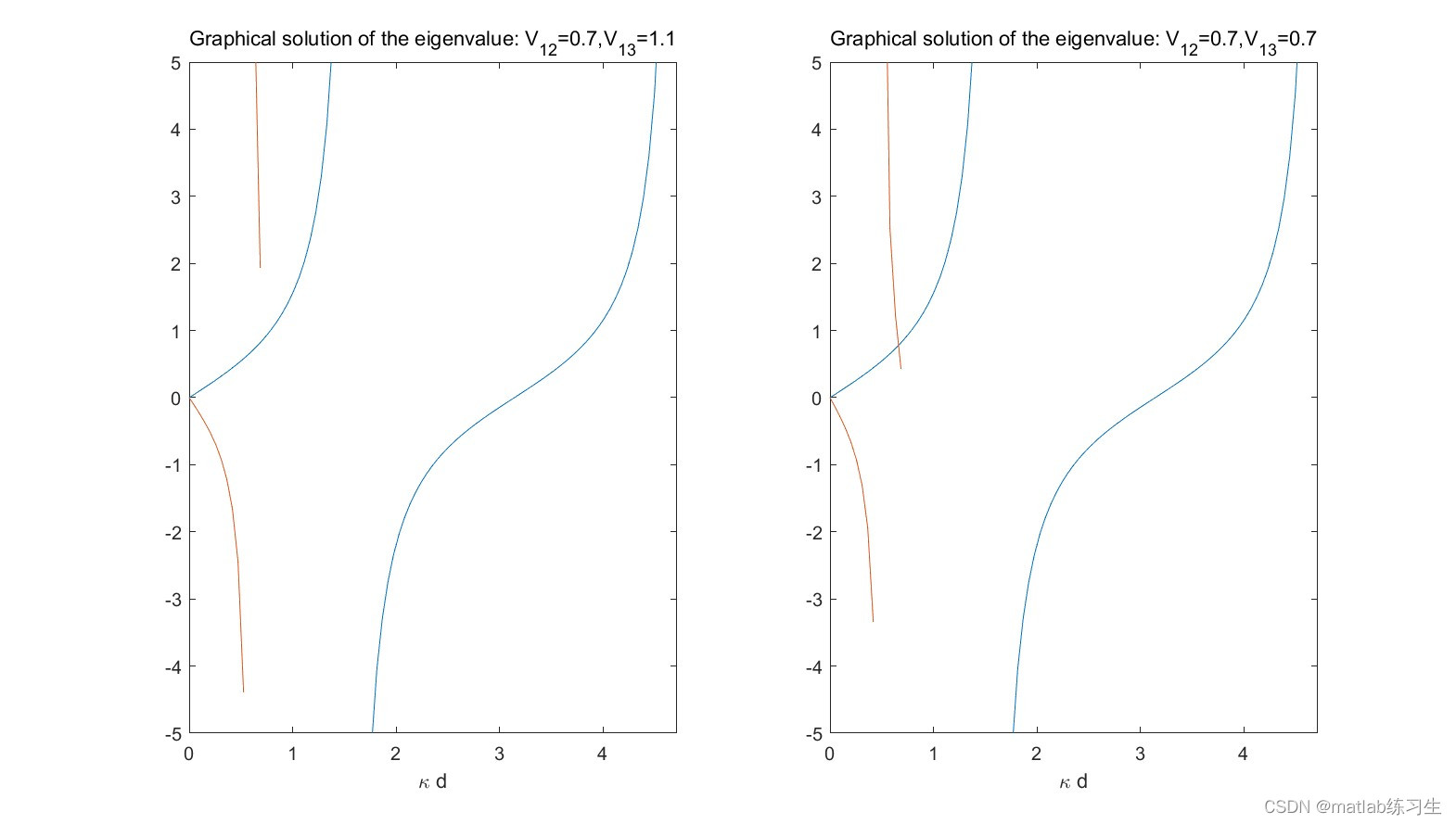
可以看出，对称光波导在tan(x)函数的第一个周期内，存在一个交点。这是因为在零点处F(x)的值为0，在第一个奇点处左侧趋近于-∞，右侧趋近+∞，在临界值附近再次趋近于0

这相当于在整个y轴范围内都存在数值，和tan(x)函数必然相交。

反过来，非对称波导不一定存在同样的特性，如左图所示吗，没有交点。

既然能算出模式的解，自然可以用matlab绘制出TM模式的模场分布：

通过电磁理论求解一定边界条件下的麦克斯韦方程组，并得到电磁场的表达式如下：

$\ E_y=Ae^{-\delta x}, x\geq0$

$E_y=A\left[\cos{\left(\kappa x\right)}-\frac{\delta}{\kappa}\sin{\left(\kappa x\right)}\right],-d\le x\le0\$

$E_y=\left[\cos{\left(\kappa d\right)}+\frac{\delta}{\kappa}\sin{\left(\kappa d\right)}\right], x\le-d\$

程序代码如下：

Np = 1001;
x2 = linspace(-2*d,-d,Np);
x1 = linspace(-d,0,Np);
x3 = linspace(0,d,Np);

Ey1 = zeros(Np,3);
Ey2 = Ey1;
Ey3 = Ey2;

for m = 1:3 %分别计算1、2、3阶
    Ey1(:,m) = cos(kappa(m)*x1)-delta(m)/kappa(m)*sin(kappa(m)*x1);
    Ey2(:,m) = (cos(kappa(m)*d)+delta(m)/kappa(m)*sin(kappa(m)*d))*exp(gamma(m)*(x2+d));
    Ey3(:,m) = exp(-delta(m)*x3);
end

figure
Ey = [Ey2;Ey1;Ey3];
Ey = Ey/diag(max(abs(Ey)));
x = [x2';x1';x3'];
plot(x,Ey(:,1),'-',x,Ey(:,2),'--',x,Ey(:,3),':','LineWidth',2)
legend('TE_0','TE_1','TE_2')
xlabel('x')
axis([x(1) x(end) -1.1 1.1])
hold on 
plot([-d,-d],[-1.1,1.1],'black--')
plot([0,0],[-1.1,1.1],'black--')
plot([x(1),x(end)],[0,0],'black')

结果：

注意矩阵拼接时候的行列对应。