Pyomo介绍

      Pyomo：全称Python Optimization Modeling Objects，优化建模工具，是一个基于Python的开源软件包，支持多种优化功能，用于制定和分析优化模型(optimization models)。Pyomo可用于定义符号问题(symbolic problems)、创建具体问题实例(create concrete problem instances)，并使用标准求解器解决这些实例。Pyomo包含一个pyomo命令，可自动构建和优化模型。源码地址：https://github.com/Pyomo/pyomo ，license为BSD，最新发布版本为6.9.1。

      Pyomo支持多种问题类型，包括：

      (1).Linear programming(线性规划)

      (2).Quadratic programming(二次规划)

      (3).Nonlinear programming(非线性规划)

      (4).Mixed-integer linear programming(混合整数线性规划)

      (5).Mixed-integer quadratic programming(混合整数二次规划)

      (6).Mixed-integer nonlinear programming(混合整数非线性规划)

      (7).Mixed-integer stochastic programming(混合整数随机规划)

      (8).Generalized disjunctive programming(广义析取规划)

      (9).Differential algebraic equations(微分代数方程)

      (10).Mathematical programming with equilibrium constraints(具有平衡约束的数学规划)

      (11).Constraint programming(约束规划)

      安装Pyomo，执行命令：pip install pyomo

      GLPK：GNU Linear Programming Kit，是开源的线性规划求解器，适用于线性问题，线性规划中会用到。从 https://sourceforge.net/projects/winglpk/ 下载winglpk-4.65.zip，解压缩，并将D:\soft\winglpk-4.65\glpk-4.65\w64目录添加到系统环境变量中。

      这里参考 https://github.com/Pyomo/pyomo-gallery 中的线性规划问题示例，简单说明Pyomo的使用。Diet Problem是经典的线性规划问题，目标是选择一组食物，以最低的成本满足营养需求。

      Diet Problem可以用以下模型在数学上表述为线性规划问题：

      测试代码如下：在原有基础上，新加入了约束条件，即从所有食物中必须选择5种食物

from pyomo.environ import *
infinity = float('inf')
ninfinity = float('-inf')

# 1. creating a model object
model = AbstractModel()

# 2. F and N are declared abstractly using the Set component
model.F = Set() # Foods
model.N = Set() # Nutrients

# 3. the model parameters are defined abstractly using the Param component
model.c    = Param(model.F, within=PositiveReals) # Cost of each food
model.a    = Param(model.F, model.N, within=NonNegativeReals) # Amount of nutrient in each food
model.Nmin = Param(model.N, within=NonNegativeReals, default=0.0) # Lower bound on each nutrient
model.Nmax = Param(model.N, within=NonNegativeReals, default=infinity) # Upper bound on each nutrient
model.V    = Param(model.F, within=PositiveReals) # Volume per serving of food
model.Vmax = Param(within=PositiveReals) # Maximum volume of food consumed

# 4. Var component is used to define the decision variables
model.x = Var(model.F, within=NonNegativeIntegers) # Number of servings consumed of each food
model.y = Var(model.F, within=Binary) # decide whether to choose this food

# 5. Objective component is used to define the cost objective
def cost_rule(model): # Minimize the cost of food that is consumed
    return sum(model.c[i]*model.x[i] for i in model.F)
model.cost = Objective(rule=cost_rule, sense=minimize)

# 6. rule functions are used to define constraint expressions in the Constraint component:
def nutrient_rule(model, j): # Limit nutrient consumption for each nutrient
    value = sum(model.a[i,j]*model.x[i] for i in model.F)
    return inequality(model.Nmin[j], value, model.Nmax[j])
model.nutrient_limit = Constraint(model.N, rule=nutrient_rule)

def volume_rule(model): # Limit the volume of food consumed
    return sum(model.V[i]*model.x[i] for i in model.F) <= model.Vmax
model.volume = Constraint(rule=volume_rule)

def select_rule(model):
    return sum(model.y[i] for i in model.F) == 5
model.select = Constraint(rule=select_rule)

def linking_upper_rule(model, f):
    return model.x[f] <= model.y[f] * 1e6
model.linking_upper = Constraint(model.F, rule=linking_upper_rule)

def linking_lower_rule(model, f):
    return model.x[f] >= model.y[f]
model.linking_lower = Constraint(model.F, rule=linking_lower_rule)

      执行命令如下：

pyomo solve --solver=glpk test_pyomo_linear_programming.py ../test_data/diet.dat

      执行结果如下图所示：没有增加约束条件时，成本为15.05；增加约束条件后成本为15.4

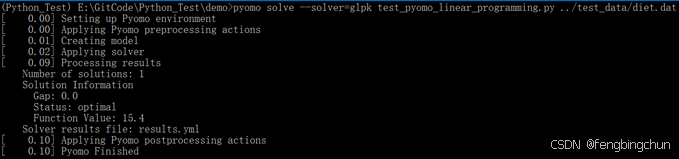
      执行完后会生成results.yml文件，内容如下：

# ==========================================================
# = Solver Results                                         =
# ==========================================================
# ----------------------------------------------------------
#   Problem Information
# ----------------------------------------------------------
Problem: 
- Name: unknown
  Lower bound: 15.4
  Upper bound: 15.4
  Number of objectives: 1
  Number of constraints: 28
  Number of variables: 18
  Number of nonzeros: 121
  Sense: minimize
# ----------------------------------------------------------
#   Solver Information
# ----------------------------------------------------------
Solver: 
- Status: ok
  Termination condition: optimal
  Statistics: 
    Branch and bound: 
      Number of bounded subproblems: 41
      Number of created subproblems: 41
  Error rc: 0
  Time: 0.02000141143798828
# ----------------------------------------------------------
#   Solution Information
# ----------------------------------------------------------
Solution: 
- number of solutions: 1
  number of solutions displayed: 1
- Gap: 0.0
  Status: optimal
  Message: None
  Objective:
    cost:
      Value: 15.4
  Variable:
    x[Cheeseburger]:
      Value: 3
    x[Fish Sandwich]:
      Value: 1
    x[Fries]:
      Value: 5
    x[Ham Sandwich]:
      Value: 1
    x[Lowfat Milk]:
      Value: 4
    y[Cheeseburger]:
      Value: 1
    y[Fish Sandwich]:
      Value: 1
    y[Fries]:
      Value: 1
    y[Ham Sandwich]:
      Value: 1
    y[Lowfat Milk]:
      Value: 1
  Constraint: No values

      GitHub：https://github.com/fengbingchun/Python_Test