牛顿-拉夫逊简单解释

核心：

牛顿-拉夫逊法在数学上是求解非线性代数方程式的有效方法。

其要点是把非线性方程式的求解过程变成反复地对相应的线性方程式进行求解的过程，即通常所称的逐次线性化过程。是数值计算普遍使用的重要方法，以开方运算为例，求平方根不是四则运算，因此在计算机上求平方根使用牛顿-拉夫逊迭代法来转化为四则运算进行求解。

将非线性代数方程组

                                   (1)

   在待求量  的某一个初始估计值 附近，展开成泰勒级数并略去二阶及以上的高阶项，得到线性化方程组

                         (2)

  称为牛顿法的修正方程式

由上式根据初值   可求得第一次迭代的修正量

           (3)

将 和 相加，得到变量的第一次改进值

牛顿法求解的迭代格式为

      (4)

       (5)

(4) 和（5）两式中  是函数 关于 的一阶偏导数矩阵

即jacobi matrit雅可比矩阵      是迭代次数

牛顿法当初值  和方程的精确解足够接近时，具有平方收敛特性。 

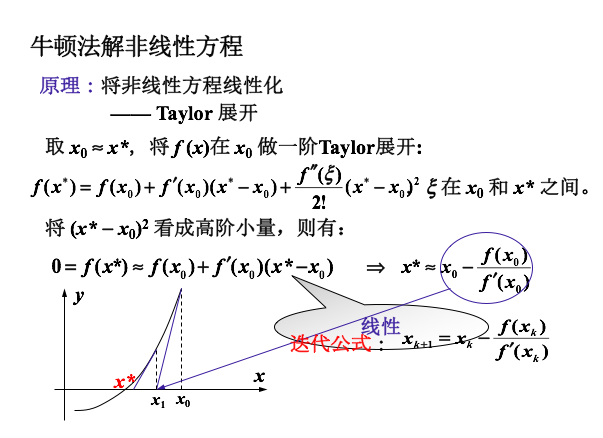
如下图：

所求  ，经常被拿来，做cost function 

如果上面的解释仍然不是很明确的话，下面给出更详细清楚的说法

假定  a > 0 ,求  等价于解方程

给定一个初始近似值  令

  是一个校正量，称为增量，于是

    即  

由于  是一个小量，如果省略高阶项    ，则得到

即 

于是 

这里 不是 的真值， 但是是真值  的 进一步近似，重复以上过程可得到迭代公式

        

逐次求得        若

则 ，容易证明序列对于任意 均收敛

简单python 2.7代码如下：

x=float(input("sqrt root for:"))

guess=20
while abs(guess*guess-x)>0.05:
    guess=(guess + x/guess)/2
    print(guess,guess*guess)
print guess

改变 guess 以及 近似误差(epsilon)，都会对求解过程产生影响。

以下贴一个二分查找求平方根:

def pow(x,epsilon):
    numGuesses=0
    low=0.0
    high=x
    ans=(high + low)/2.0
    while abs(ans**2 - x)>=epsilon:
        numGuesses +=1
        print "high is " + str(high) + " low is " + str(low) + " ans " + str(ans)
        if ans**2 <x:
            low = ans
        else:
            high=ans
        ans=(high + low)/2.0
    print ans 
    print numGuesses

改变 guess 以及 近似误差，都会对求解过程产生影响。