ACM_kruscal 计算最小生成树

算法作用

计算最小生成树
生成树: 将一个图的顶点不变, 通过去除一些边, 使它成为一棵树
最小生成树: 所有生成树中的边权和最小的生成树
比如下面图1的最小生成树是图2

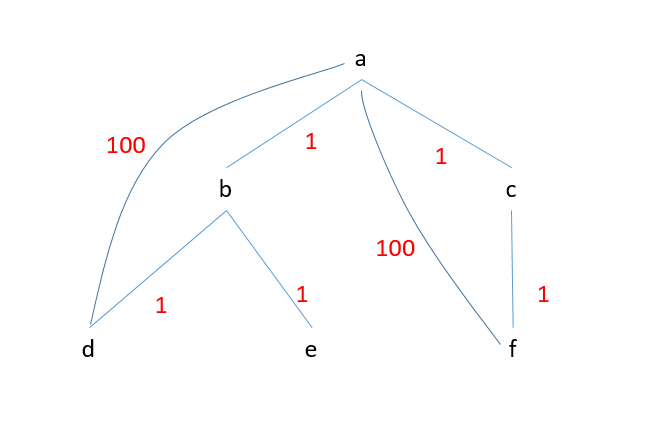
图1

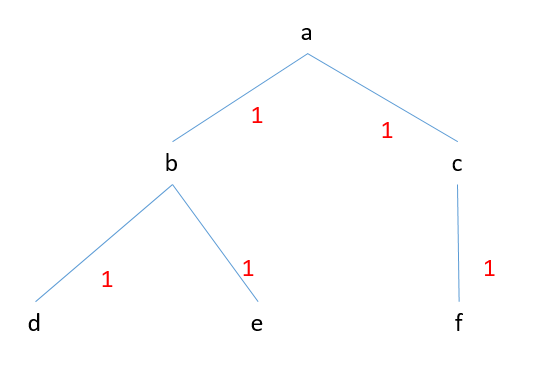
图2

时间复杂度

O(ElogE)E是边数

代码实现

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1e5 + 10;
const int M = 1e5 + 10;
int pa[N];

struct Edge {
    int from, to, cost;
    bool operator < (const Edge & rhs) const {
        return cost < rhs.cost;
    }
};

Edge oldEdge[N], newEdge[N];

int find(int x) {
    return x == pa[x] ? x : pa[x] = find(pa[x]);
}

void readData();

int main() {
    readDate();
    for(int i = 0; i < n; ++i)
        pa[i] = i;
    int cnt = 0;
    sort(oldEdge, olEdge + m);
    for(int i = 0; i < m; ++i) {
        int fx = find(oldEdge[i].from);
        int fy = find(oldEdge[i].to);
        if(fx == fy) continue;
        pa[fx] = fy;
        newEdge[cnt++] = oldEdge[i];
    }
}

其中oldEdge是老图, newEdge是新图, n是顶点数, m是边数, pa是用来实现并查集的父亲指向
代码的主体部分仅两个
1. sort的排序函数
2. find的并查集查找函数(包括后面的合并操作)
其中以前的图以边的方式存储在oldEdge中, 得到的新图的边同样以边的方式存在newEdge中, 如果想用邻接矩阵, 邻接表或者链式前向星等, 转化一下即可

算法拓展

某些看似和路径无关的可以转移过来, 看个人灵活性了吧

算法证明

算法的基本思想是: 从最小的边开始, 一直找, 不停的合并到新图中, 直到遍历所有边
证明: 反证法
设由Kruskal算法生成的T0序列为e1, e2, e3 … ev-1，假设其不是最小生成树。任意最小生成树T定义函数f(T)：T0中不存在于T中边在T0的下标。设T1是使f(T)最大的变量，设f(T1)=k，即ek不存在于T1中，T1为树且ek不在T1中，所以由引理1得T1+ek必存在圈C，C上必有e,k ≠ek，e,k不在T0 中。现令T2 = T1 - e,k + ek，则T2也为生成树但由Kruskal算法可知ek是使e1, e2 … ek-1, ek无圈的权值最小的边，e1, e2 … ek-1, e,k是树的子图必无圈故e,k的权值必定小于ek，即T2的总权值不大于T1的权值，因T1是最小生成树，故必T2也是最小生成树，但f(T2)＞k与k是f函数最大取值矛盾，故T0是最小生成树。

代码实现的具体过程及思路

主要就两个过程
先sort一下, 然后不断的选最小的边来进行扩展, 知道用完所有的边
要点无非两个:
1. sort, 使用stl中的sort即可(用的是归并排序, 时间复杂度是ElogE)
2. 并查集算法, 这个在我以前写的一篇博客中详细介绍了这种算法, 链接如下
http://blog.csdn.net/fkjslee/article/details/48809903

复杂度证明

第一个复杂度来自sort, stl中的归并排序, 复杂度ElogE, 没什么好解释的
第二个复杂度来自并查集, 并查集的一次查找的复杂度是反阿克曼函数, 近似等于O(1), 一个会查找E* 2次, 所以复杂度是O(E)
所以总的复杂度是O(ElogE)