k-近邻算法(k-Nearest Neighbor，KNN)

算法介绍

所谓K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例（也就是上面所说的K个邻居）， 这K个实例的多数属于某个类，就把该输入实例分类到这个类中。根据这个说法，咱们来看下引自维基百科上的一幅图：

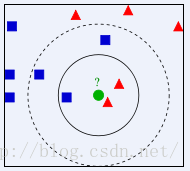
如 上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说，现在，我们不知道中间那个绿色的数据是从属于哪一类（蓝色小正方形or红色小三角形），下面，我们就要解决这个问题：给这个绿色的圆分类。

·            如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。

·            如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。

关于kNN的python实现流程如下所示：

1、设定标签和验证数据的比例（例如0.5，那么就是0-499作为测试数据，500-999作为已分类验证数据）；

2、将数据进行归一化处理（归一化处理是按照列数据进行，例如3列数据，先找到每列数据的最大值max和最小值min，计算它的跨度range=max-min,再将此列里面的每个数据除以range得到）；

3、判断分类是遍历所有的测试数据，例如按照第一步所阐述的0-499作为测试数据，500-999作为已分类验证数据，具体代码如下：

def datingClassTest():
    hoRatio = 0.50      #hold out 10%
   datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')       #load data setfrom file
    normMat, ranges,minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs =int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult =classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
       if (classifierResult != datingLabels[i]): errorCount += 1.0
//normMat[numTestVecs:m,:]这个就是取normMat[500:1000,:]的数据。

4、进行数据分类（将待分类的数据和所有已分类的数据进行一次欧氏距离计算，按照计算距离从小到大排列，选择最近的K个已分类数据对待分类数据进行贴标签，最后选择标签最多的那个作为待分类数据的类别），代码实现如下：

def classify0(inX, dataSet, labels, k):
    dataSetSize =dataSet.shape[0]
    diffMat = tile(inX,(dataSetSize,1)) - dataSet
    sqDiffMat = diffMat**2
    sqDistances =sqDiffMat.sum(axis=1)
    distances =sqDistances**0.5
     //以上计算欧氏距离
    sortedDistIndicies =distances.argsort()    
    //按照欧式距离从小到大排列，取数组的下标作为值
    classCount={}         
    //计算K次数据
    for i in range(k):
        voteIlabel =labels[sortedDistIndicies[i]]
       classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
//按照分类标签数从大到小排列
    sortedClassCount =sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
//返回最大的分类标签
return sortedClassCount[0][0]

优点

1.简单，易于理解，易于实现，无需估计参数，无需训练；

2. 适合对稀有事件进行分类；

3.特别适合于多分类问题(multi-modal,对象具有多个类别标签)， kNN比SVM的表现要好。

缺点

该算法在分类时有个主要的不足是，当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。

该方法的另一个不足之处是计算量较大，因为对每一个待分类的文本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。