优化

问题定义

目标函数为$min f(x)$

梯度下降

一阶方法
$f(x)$在$x_k$的一阶泰勒级数展开：

$$f(x_{k+1})=f(x_k+\Delta x_k) \approx f(x_k)+f(x_k)'\Delta x_k$$

momentum

通过积累下降速度，来加速梯度下降方法。这时学习率（学习速度）变复杂。

牛顿法

二阶方法
对$f(x)$在$x_k$处进行二阶泰勒展开

$$f(x_{k+1})=f(x_k+\Delta x)\approx f(x_k)+f'(x_k)\Delta x+\frac 12 \Delta x^T H(f)\Delta x$$
其中， $H(f)$是 $f(x)$的所有二阶导数构成的矩阵.我们的目标是求上式得最小值，所以按照惯例对 $\Delta x$其求导： $$f'(x_k)+H(f)\Delta x=0$$ 得到迭代更新量 $$\Delta x=-\frac{f'(x_k)}{H(f)}$$ 牛顿法利用了二阶导数，对于二次函数的最小化问题能够一步收敛。由于需要计算Hessian矩阵，对于非二次函数的高纬问题，计算、存储开销为 $O(n^2)$，而且对于使用BP方式计算梯度的神经网络来说，我们可能根本不知道如何计算Hessian矩阵。而共轭梯度下降是无需要计算Hessian矩阵的方法。

共轭梯度下降（Conjugate gradient）

二阶方法。使用梯度下降可能存在在相同的方向上多次迭代，如下图绿线所示：

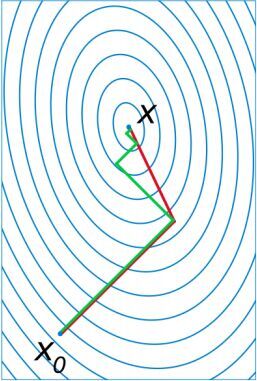
共轭梯度方法不选择准确的梯度方向为它的前进方向，从不在相同的方向上迭代两次，如上图中红线所示。
对于目标函数$f(x)$为二次的情况，可以写为:

$$f(x)=\frac12x^TAx+b^Tx+c$$ ,并且总可以找到 $A$满足对称性：$A=A^T$，求 $\nabla f(x)$: $$\nabla f(x) = A x + b,$$
梯度下降和共轭梯度下降方法对比如下：

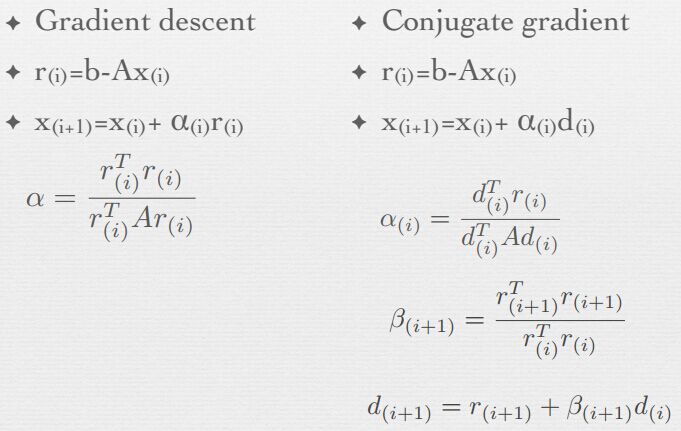
计算问题

不用计算hesse矩阵

学习率

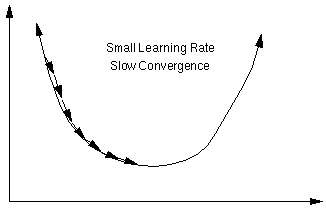
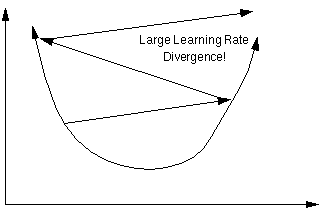
学习率过小，收敛速度慢；学习率过大，可能导致网络的损失函数值不降反增。如下图：

根据学习率随训练迭代的变化方式分为两种：非自适应和自适应。

非自适应

一般地，学习率随着训练迭代增加而减小，其形式包括很多种，如
退火方法（Annealing schedule，如指数退火法），或者其他自定义的衰减方式。
caffe中使用的learning rate 下降方式，详见这里。

自适应

Adagrad

Adadelta

RMSprop

Adam

Adaptive Moment Estimation

以上详细见本部分的参考2

参考

1.Learning Rate Schedules for Faster Stochastic Gradient Search, Christian Darken, Joseph Chang and John Moody, Neural Networks for Signal Processing 2 — Proceedings of the 1992 IEEE Workshop, IEEE Press, Piscataway, NJ, 1992.
2.http://sebastianruder.com/optimizing-gradient-descent/
3.http://cs231n.github.io/neural-networks-3/#anneal

参考

共轭梯度：
1.bengio,etc,Deep Learning,2015
2.Jonathan Richard Shewchuk,An Introduction to the Conjugate Gradient Method Without the Agonizing Pain,1994
3.http://andrew.gibiansky.com/blog/machine-learning/conjugate-gradient/