目录
一. 特殊矩阵的输入
1.1 数值矩阵的输入
生成m✖️n零矩阵，单位矩阵以及幺模矩阵，MATLAB格式如下：
A=zeros(m,n);
B=ones(m,n);
C=eye(m,n);
生成和矩阵D同样位数的零矩阵，MATLAB格式如下：
E=zeros(size(D));备注：幺模矩阵的行列式|det(U)|=1
1.2 随机元素矩阵
如果矩阵中的元素满足[0,1]区间上的均匀分布，可利用此生成n✖️m阶均匀分布的伪随机数矩阵，MATLAB格式如下：
A=rand(n,m);1.3 对角元素矩阵
已知向量生成对角矩阵的MATLAB格式，如下：
A=diag(V);
数学形式的解释如下：
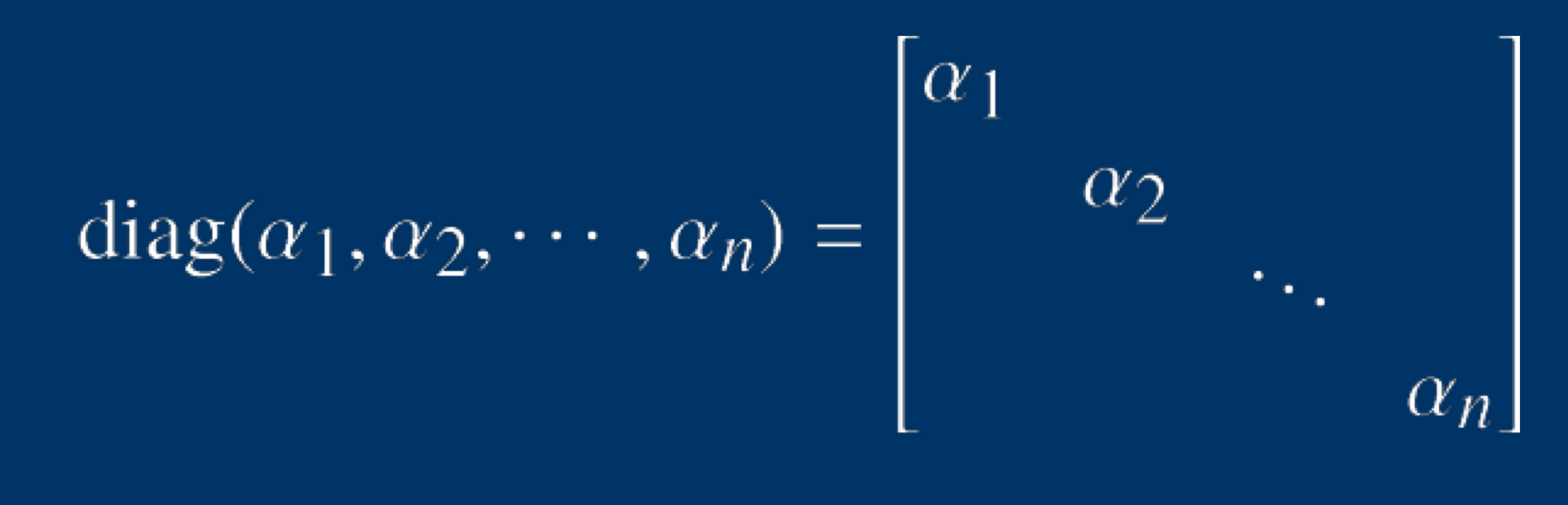
逆过来，已知矩阵提取对角元素列向量，方法一样：
V=diag(A);还有一种特殊形式，可以生成主对角线上面第k条对角线为V的矩阵，MATLAB格式：
A=diag(V,k);例题1
此例题主要研究diag()函数不同的调用格式。
（1）由行向量生成对角矩阵
代码：
C=[1,2,3];
V=diag(C)运行结果：
V =
1 0 0
0 2 0
0 0 3
（2）由列向量通过转置变成行向量
代码：
C=[1,2,3];
V=diag(C);
V1=diag(V)' %此处的V为对角矩阵，也可以看成列向量运行结果：
V1 =
1 2 3
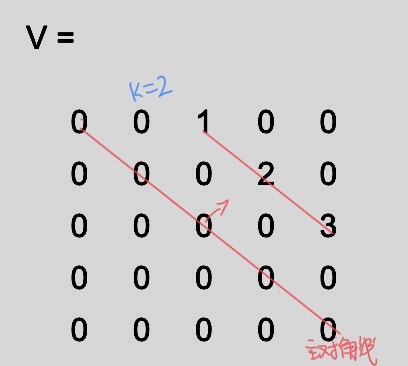
（3）主对角线上面第k条对角线为向量C的矩阵
代码：
C=[1,2,3];
V=diag(C,2)运行结果：
V =
0 0 1 0 0
0 0 0 2 0
0 0 0 0 3
0 0 0 0 0
0 0 0 0 0
分析如下：
例题2
利用diag()函数生成三对角矩阵，如下：
解：
MATLAB代码如下：
V=diag([1 2 3 4])+diag([2 3 4],1)+diag([5 4 3],-1)
%主对角线上一行与下一行运行结果：
V =
1 2 0 0
5 2 3 0
0 4 3 4
0 0 3 4
二. Hilbert矩阵及逆Hilbert矩阵
Hilbert矩阵一定是一个方阵，数学表达形式如下：
矩阵中第（i,j)个元素的值可用如下形式表示：
生成n阶的Hilbert矩阵，MATLAB格式如下：
A=hilb(n)求它对应的逆Hilbert矩阵，MATLAB格式如下：
B=invhilb(n)三. Hankel(汉克）矩阵
Hankel矩阵的数学形式，如下：
经过观察发现，第一列和最后一行的数据就可以代表整个矩阵中的所有元素。MATLAB格式如下：
%提前给定两个向量C和R
H=hankel(C,R)观察可发现，第一列的各个元素为C向量，最后一行各个元素定义为R。很明显H为一个对称矩阵。
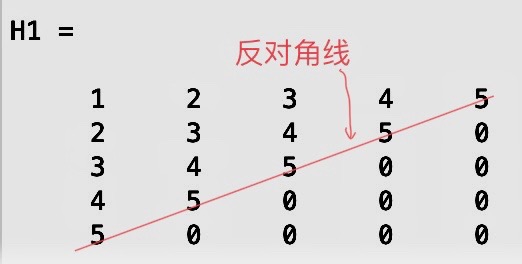
如果只给定一个向量，如下格式：
H1=hankel(C)
则此Hankel矩阵反对角线上元素相等，且反对角线下元素均为零。
MATLAB代码：
clc;clear;
C=[1 2 3 4 5];
H1=hankel(C)运行结果：
H1 =
1 2 3 4 5
2 3 4 5 0
3 4 5 0 0
4 5 0 0 0
5 0 0 0 0
分析：
四. Vandermonde（范德蒙）矩阵
范德蒙矩阵的数学形式如下：
矩阵中的第(i,j)个元素满足如下等式：
MATLAB格式：
V=vander(C)五. 伴随矩阵
P(s)为首项系数为1的多项式，表达式如下：
由多项式得到的伴随矩阵，如下：
MATLAB调用格式，如下：
B=compan(P)例题3
考虑一个多项式，利用MATLAB求出该多项式的伴随矩阵。
解：
MATLAB代码如下：
clc;clear;
P=[2 0 4 5 6];%由高次到低次的系数
A=compan(P)运行结果：
A =
0 -2.0000 -2.5000 -3.0000
1.0000 0 0 0
0 1.0000 0 0
0 0 1.0000 0
六. 符号矩阵的输入
可以由数值矩阵转换为符号矩阵，MATLAB格式如下：
B=sym(A)举例MATLAB代码：
clc;clear;
A=hilb(3) %A为Hilbert矩阵
B=sym(A) %分数形式运行结果：
A =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
B =
[ 1, 1/2, 1/3]
[ 1/2, 1/3, 1/4]
[ 1/3, 1/4, 1/5]
1140
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
