详解信号的参数估计

唠嗑！

已于 2024-01-17 22:38:42 修改

阅读量947

点赞数 2

分类专栏：信息论安全文章标签：现代信号处理网络安全

于 2022-05-17 22:05:14 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/forest_LL/article/details/124802708

版权

信息论安全专栏收录该内容

37 篇文章 17 订阅

订阅专栏

目录

一. 估计的评价准则

二. 一致估计

三. 估计均值

四. 估计方差

4.1 均值已知

4.2 均值未知

五. 估计自相关函数

5.1 无偏自相关函数估计

5.2 有偏自相关函数估计

六. 发展历程

七. 参考书籍

一. 估计的评价准则

假设a是一个广义平稳随机信号x(n)的一个特征量， $\hat a$ 代表a的一个估计量。估计的偏差可以反应估计量与真值的接近程度，定义如下：

$B=E[a-\hat a]=a-E[\hat a]$

理解：

第一个等号：真实值减去估计值的均值，即为估计的偏差

第二个等号：真实值是不变的，所以其均值为自己本身。

直观上，B越小， $\hat a$ 对a的估计就越好。理论上当样本数N趋于无穷大时，会逐渐形成无偏估计，如下：

$\lim_{N\to \infty}B=a-\lim_{N\to\infty}E[\hat a]=0$

无偏估计可直观理解为估计误差为0，根据该定义发现是一种渐近的理解（引入了数学中的极限思想），对信号处理非常有用

估计的方差可以表示各次估计值相对估计均值的分散程度。估计的方差定义如下：

$var[\hat a]=\sigma^2_{\hat a}=E\lbrace [\hat a-E(\hat a)]^2\rbrace=E[\hat a^2]-[E(\hat a)]^2$

理解：

第一个等号：方差的另一种写法

第二个等号：方差与均值的关系

第三个等号：均值的线性性质

估计的均方误差可以综合反映估计的特性，定义如下：

$E[\tilde a^2]=E[(\hat a-a)^2]$

这个是实际做实验时，最常用的一个量，来综合衡量估计算法的好坏，比如网络安全领域的MMSE估计，等等。

如果均方误差满足如下条件，则称其为一致估计，如下：

样本数 $N\to \infty$
$\lim_{N\to\infty}E[\tilde a^2]=0$

性质1考虑样本无限制下的渐近性质

性质2代表均方误差需要接近于0

二. 一致估计

本小节我们来证明一个很有用的性质。

性质：给定一致估计，证明偏差和方差都趋于零。

证明：

给定均方误差化简如下：

第一个等号：均方误差的概念

第二个等号：均值的性质

第三，四个等号：佩服

第四个等号：偏差和方差的概念

由条件可得，一致估计的均方误差为0，也就是可得：

$E[\tilde a^2]=0$

带入上面的式子化简，所以可得：

$B^2+\sigma_{\hat a}^2=0$

两个平方和为0，只能是都为0，所以最终可得偏差和方差均为0。

证明完毕。

备注说明一个概念叫有效估计，如下：

利用 $\hat a$ 代表某算法的估计值，其他算法的估计值表示如下：

$\hat a_1,\hat a_2,\cdots,\hat a_k,\cdots$

如果以下不等式恒成立：

$E(\hat a-a)^2\leq E(\hat a_k-a)^2$

则称该估计为有效估计。

有效估计需要保证该算法比其他算法的误差都要小。

三. 估计均值

利用N代表观察次数，则平稳信号序列x(n)的观察样本如下：

$x_0,x_1,\cdots,x_{N-1}$

由此可计算均值的估计：

$\hat m_x=\frac{1}{N}\sum_{i=0}^{N-1}x_i$

相加除以N，这就是普通的平均值计算公式。

3.1 偏差

首先可得：

$E[\hat m_x]=E(\frac{1}{N}\sum_{i=0}^{N-1}x_i)=\frac{1}{N}\sum_{i=0}^{N-1}E[x_i]=m_x$

由此可计算偏差：

$B=m_x-E[\hat m_x]=0$

所以此方式是一种无偏估计。

3.2 方差

根据定义可得：

$E(\hat m_x^2)=E[(\frac{1}{N}\sum_{i=0}^{N-1}x_i)(\frac{1}{N}\sum_{j=0}^{N-1}x_j)]=\frac{1}{N^2}\sum_{j=0}^{N-1}\sum_{i=0}^{N-1}E[x_ix_j]$

（1）当 $x_i$ 和 $x_j$ 互不相关时，有：

$E[x_ix_j]=E[x_i]E[x_j]=m_x^2$

代入原式子进行化简可得：

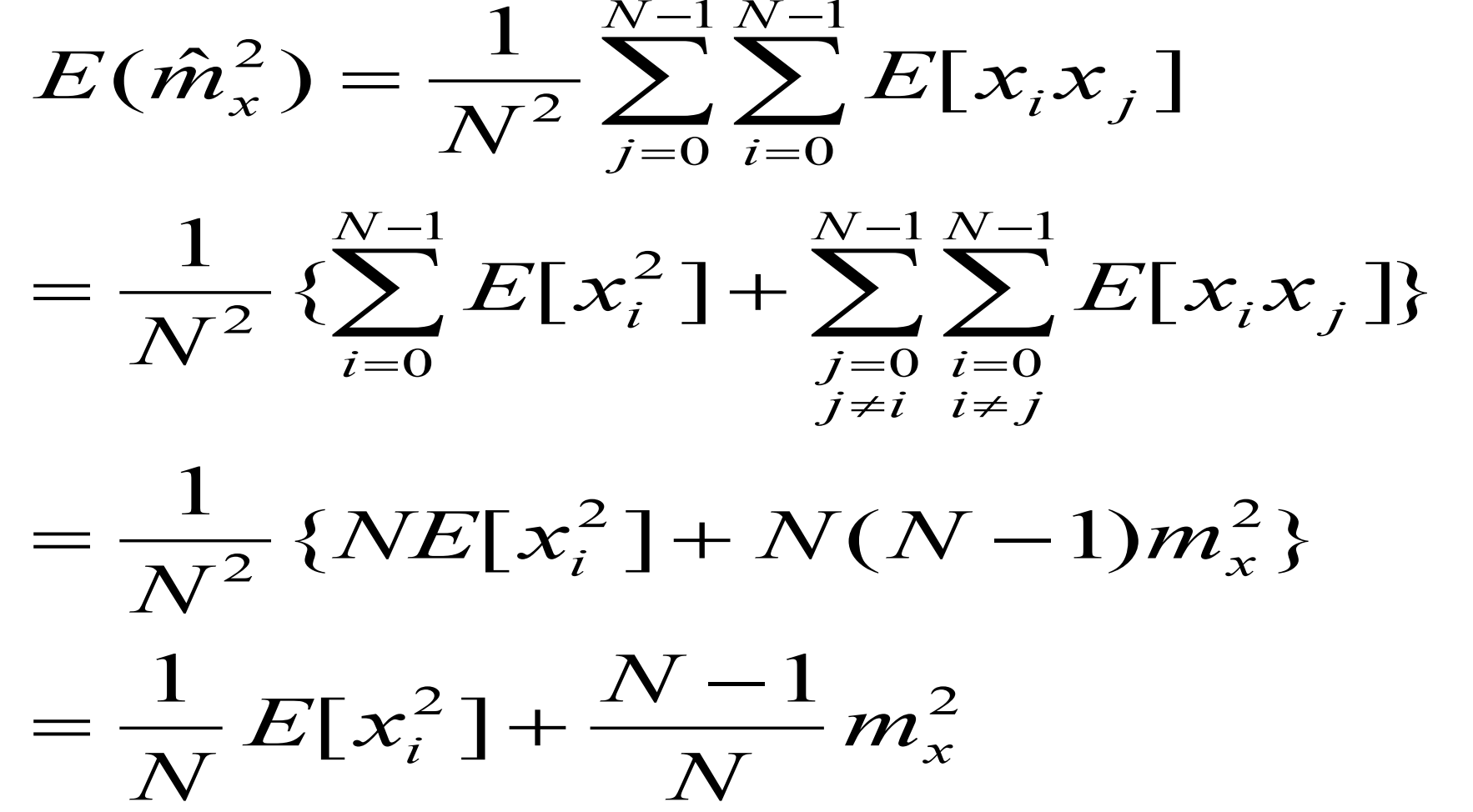
所以该估计的方差为：

$\sigma_{m_x}^2=E[\hat m_x^2]-m_x^2=\frac{1}{N}E[x_i^2]-\frac{1}{N}m_x^2=\frac{1}{N}\sigma_x^2$

可得如下极限：

$\lim_{N\to\infty}\sigma_{m_x}^2=0$

所以该估计为无偏一致估计。

（2）当 $x_i$ 和 $x_j$ 相关时，有：

$\sigma_{m_x}^2=E\lbrace [\hat m_x-E(\hat m_x)]^2\rbrace$

进一步化简可得：

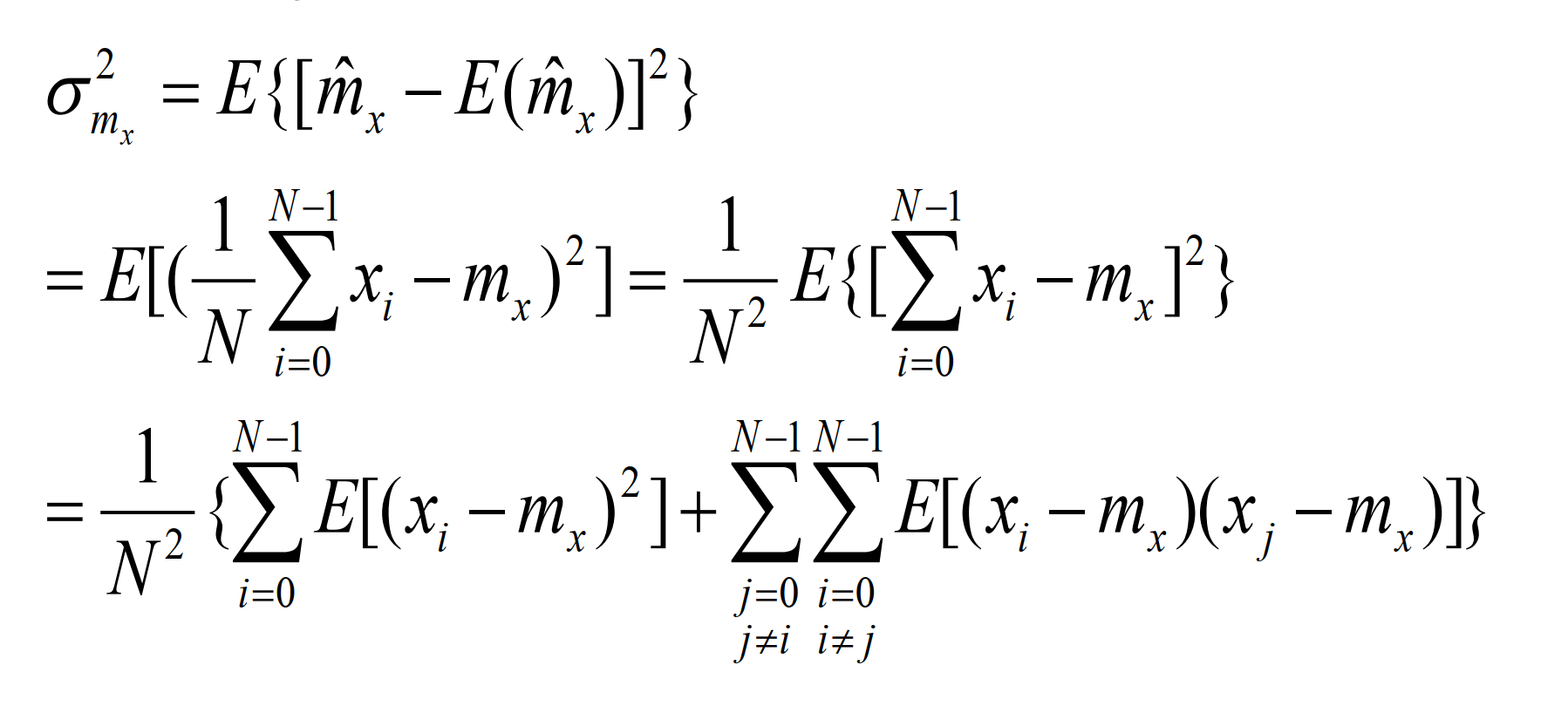
当i和j相差m时，可得：

$E[(x-m_x)(x_j-m_x)]=cov(m)$

由于在N个数据中，相距m点的数据样本有N-m对，所以可得：

当信号数据存在相关性时，估计值的方差与协方差相关，不是一致估计，当然改变N值可以改善估计方差。

四. 估计方差

4.1 均值已知

当信号均值 $m_x$ 已知，方差估计可计算得：

$\hat \sigma_x^2=\frac{1}{N}\sum_{i=0}^{N-1}(x_i-m_x)^2$

证明此式子为无偏一致估计。

解：

（1）首先验证偏差：

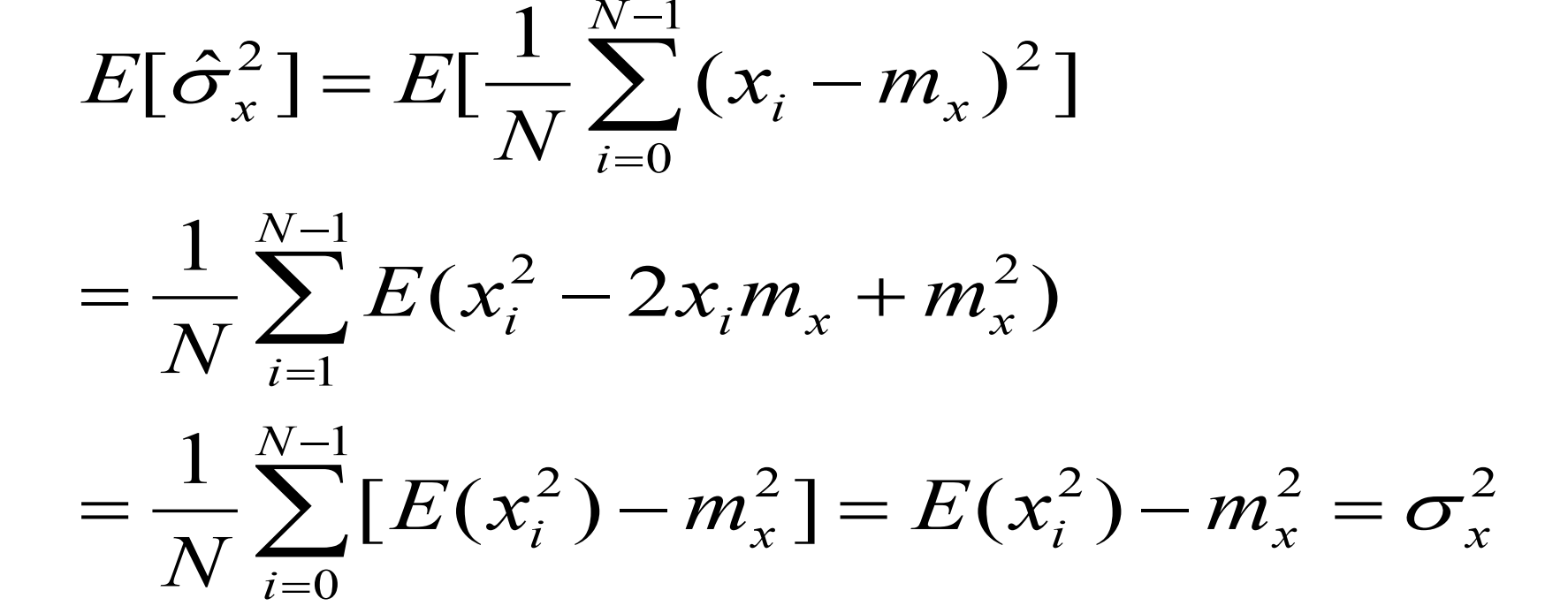
（2）接着验证一致性：

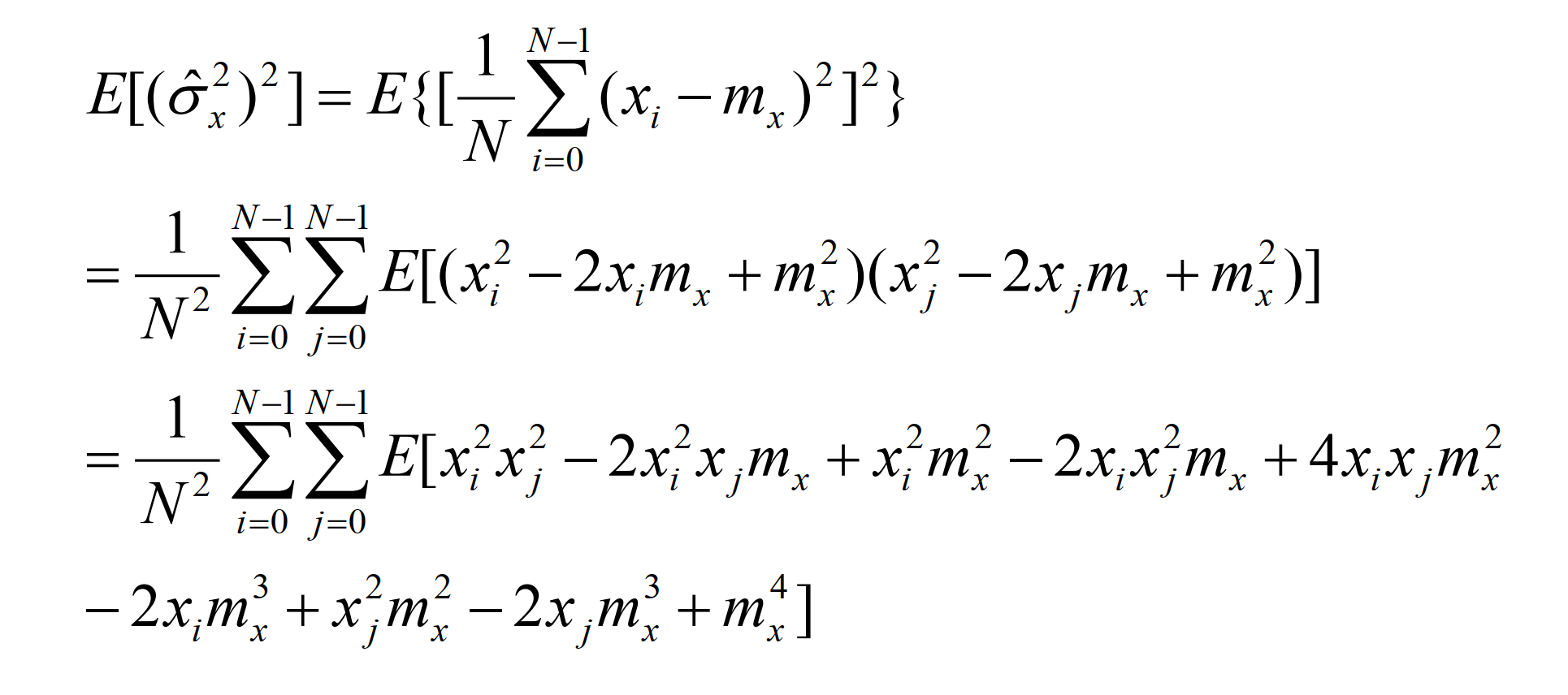
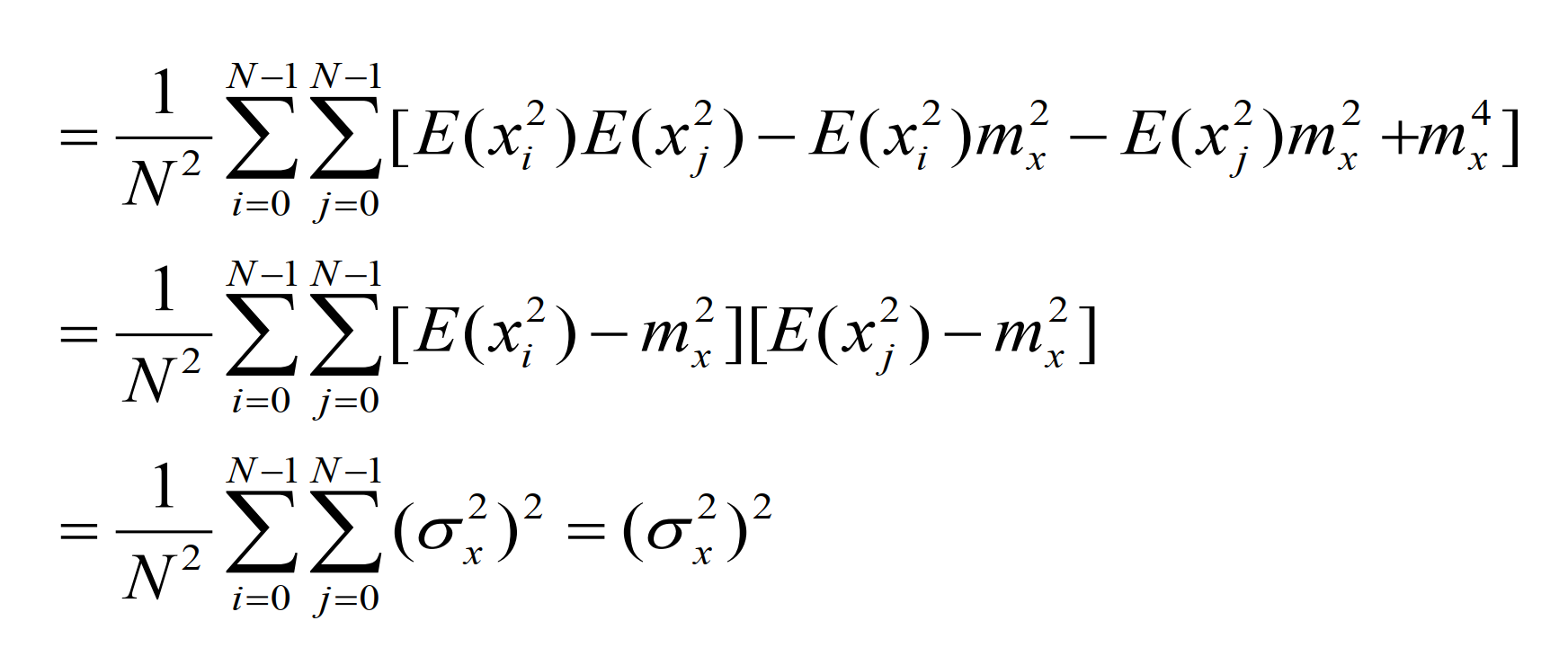
所以，估计的方差计算为：

4.2 均值未知

当估计的均值未知时， $m_x$ 用估值 $\hat m_x$ 代替，方差可估计如下：

$\hat \sigma_x^2=\frac{1}{N}\sum_{i=0}^{N-1}(x_i-\hat m_x)^2$

(1) 证明该偏差为有偏估计

（2）修改原式子，形成无偏估计

解：

（1）

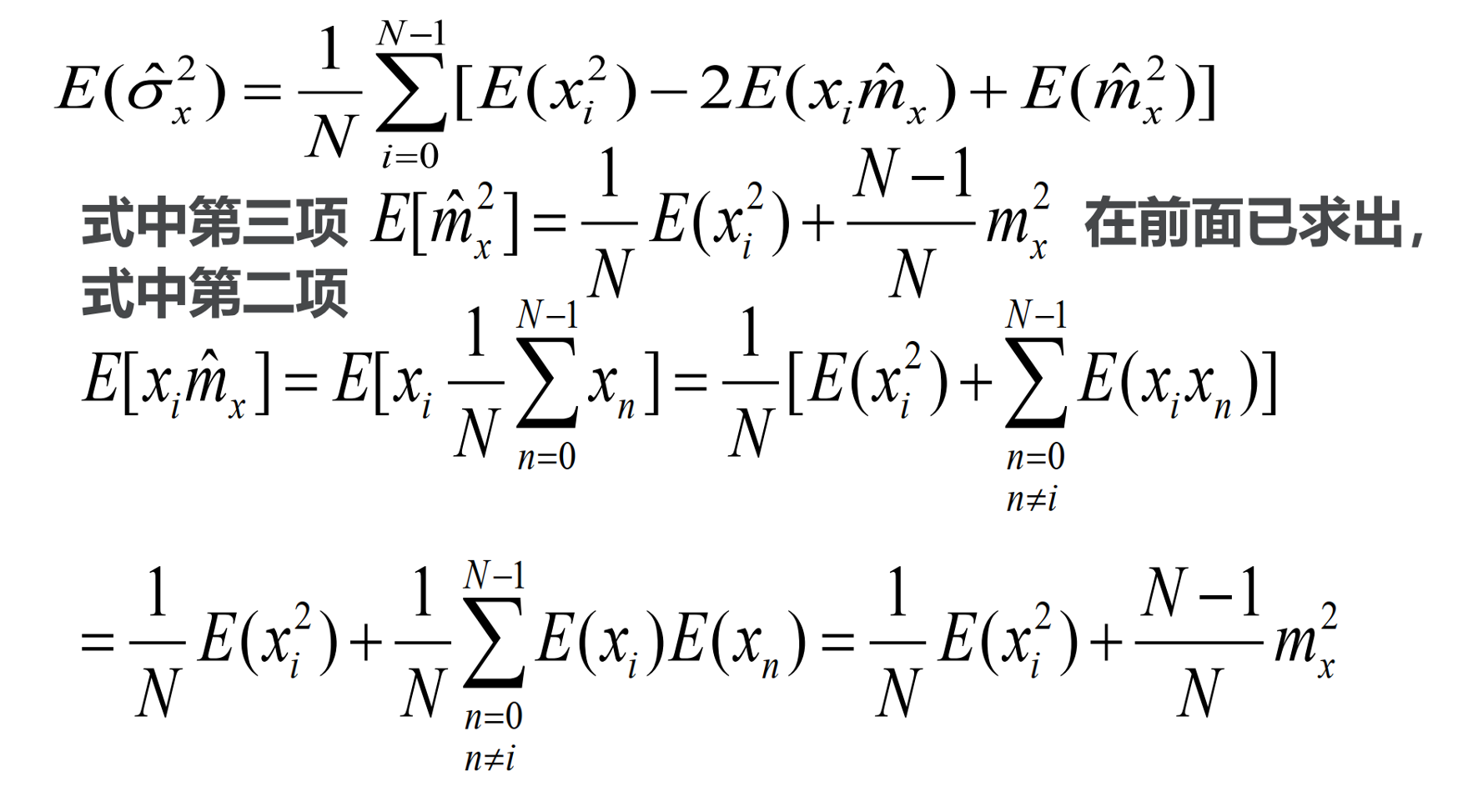
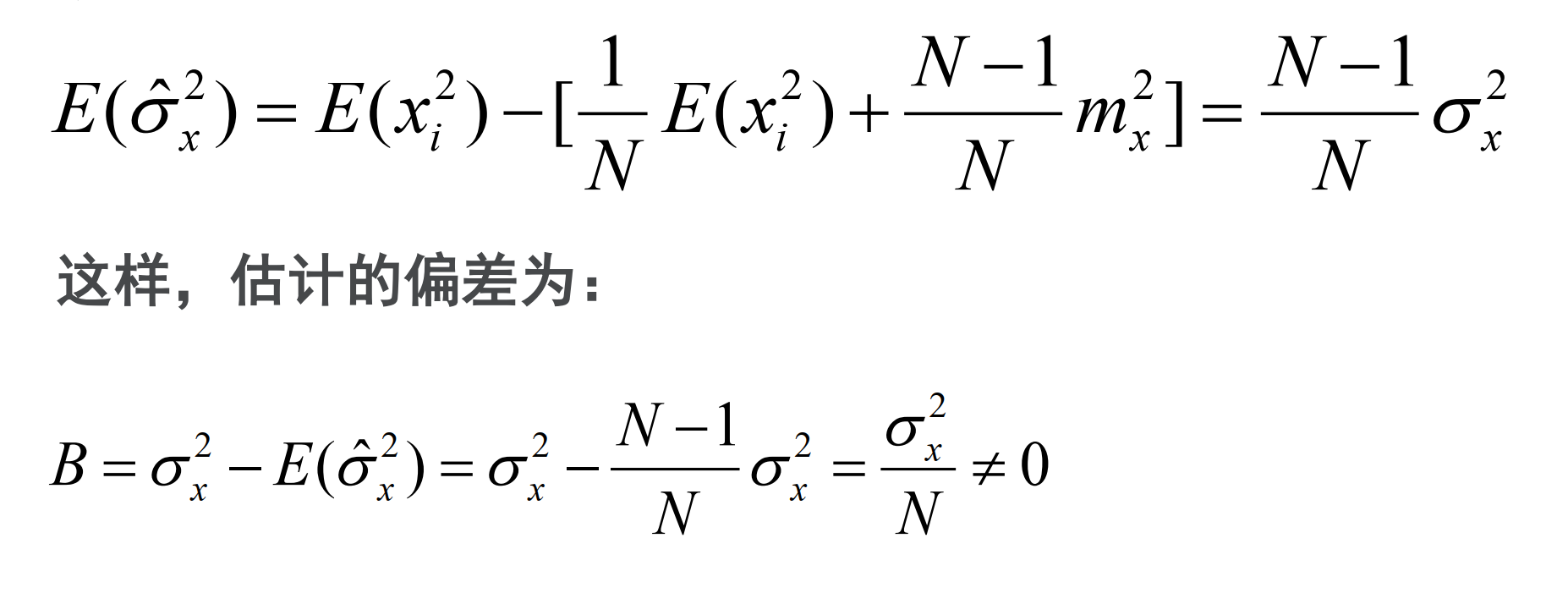
很明显此为有偏估计。

（2）无偏估计的形式如下：

$\hat \sigma_x^{'2}=\frac{1}{N-1}\sum_{i=0}^{N-1}(x_i-\hat m_x^2)^2$

以下证明此式子为无偏估计：

显然可得：

$\hat \sigma_x^{'2}=\frac{N}{N-1}\hat \sigma_x^2$

对上式子两边求均值，可得：

$E(\hat \sigma_x^{'2})=\frac{N}{N-1}E(\hat \sigma_x^2)=\sigma_x^2$

所以B=0，此为无偏估计。

五. 估计自相关函数

5.1 无偏自相关函数估计

估计公式为：

$\hat r_{xx}(m)=\frac{1}{N-|m|}\sum_{n=0}^{N-|m|-1}x(n)x(n+m)$

首先可计算：

$E[\hat r_{xx}(m)]=\frac{1}{N-|m|}\sum_{n=0}^{N-|m|-1}E[x(n)x(n+m)]=r_{xx}(m)$

由此可计算偏差为：

$B=r_{xx}(m)-E[\hat r_{xx}(m)]=0$

所以此估计为无偏估计。

估计方差的计算较复杂，可以近似可得：

当N满足如下时，方差趋于0：

$N>>m,\quad N\to\infty$

5.2 有偏自相关函数估计

估计公式如下：

$\hat r_{xx}(m)=\frac{1}{N}\sum_{n=0}^{N-|m|-1}x(n)x(n+m)$

首先可计算：

所以估计的偏差为：

$B=r_{xx}(m)-E[\hat r_{xx}(m)]=\frac{|m|}{N}r_{xx}(m)$

接着可计算：

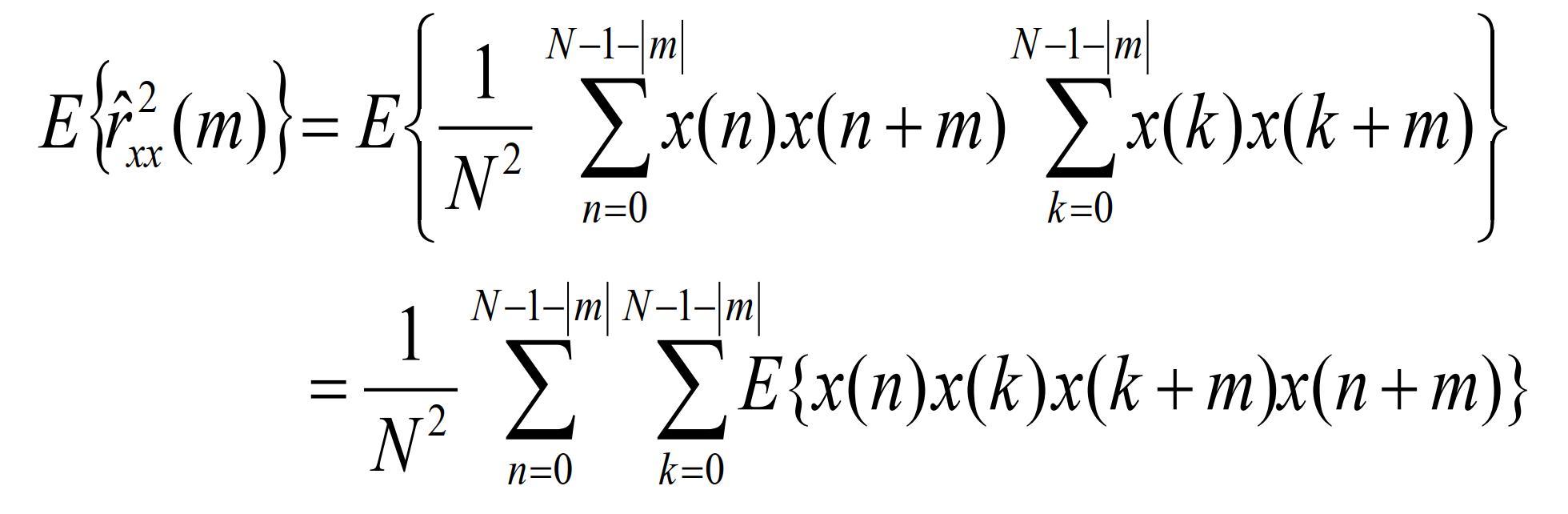
若x(n)是零均值的实高斯信号，估计的方差为：

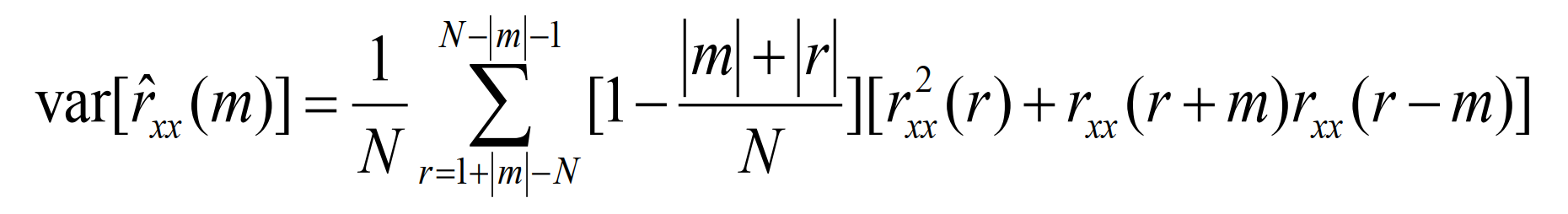
显然可得如下极限：

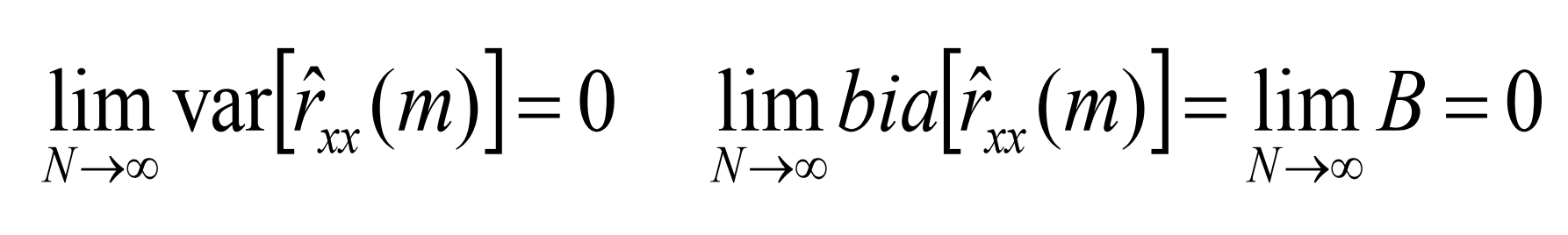
所以对于固定的m， $\hat r_{xx}(m)$ 是 $r_{xx}(m)$ 的一致估计。

有偏自相关函数估计式求傅氏变换：

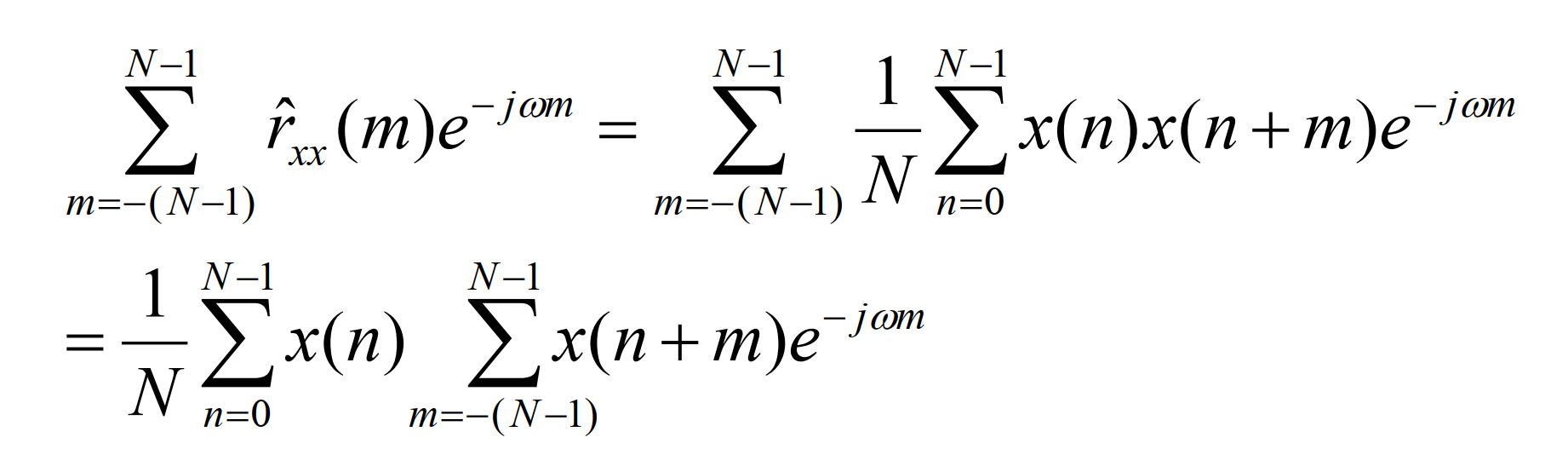
为了利用FFT计算线性卷积，可以将x(n)扩展到2N-1点的序列，如下：

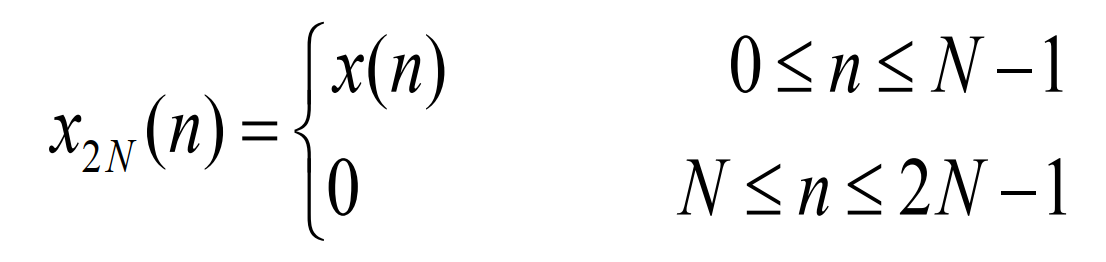
令l=n+m，可得：

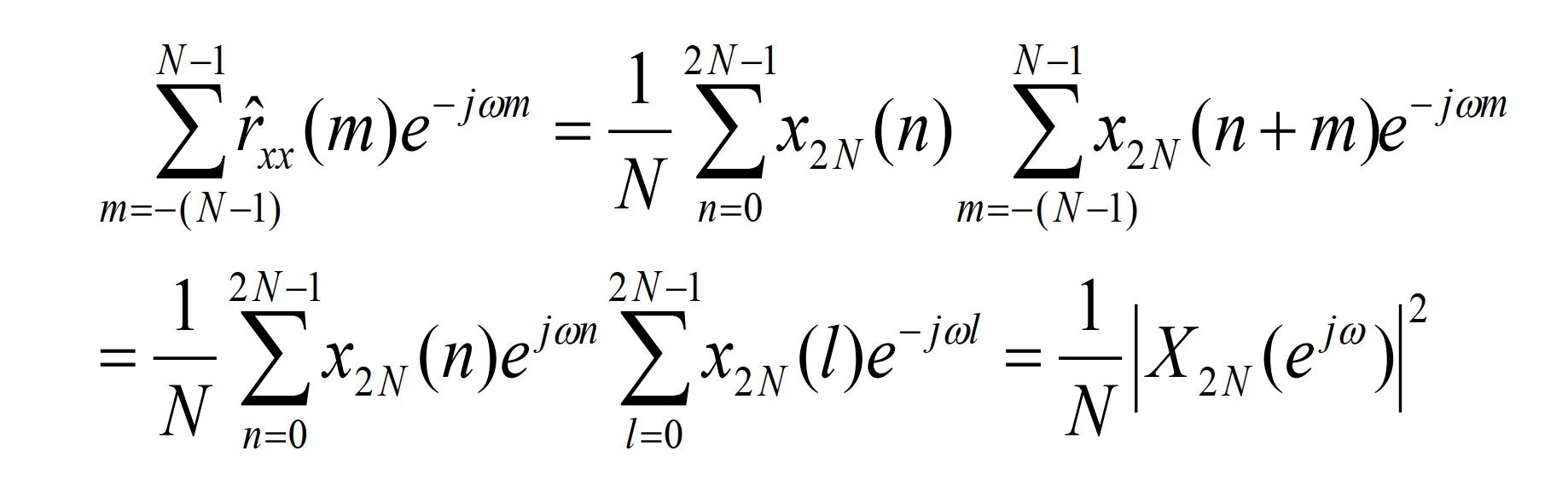
上式子中 $|X_{2N}(e^{j\omega})|^2$ 代表有限长信号的能量谱，除以N后代表功率谱。

六. 发展历程

1930s 二战时期 :初创阶段

1940s-1950s:大发展时期 (1943/D.O.North, 1942/1949/N.Wiener, 1944/S.O.Rice, 1949/P.M.Woodward)

1950s-1960s:理论成熟时期（经典的统计信号处理理论） (D.Middleton-Bayes风险理论、R.E.Kalman-滤波理论、P.J.Huber-Robust统计学、 J.P.Burg-最大熵谱估计、Capon谱估计）特征：广义平稳、高斯分布、线性问题/处理

1970s-现代统计信号处理阶段（鲁棒检测、非参量检测等）特征：非平稳、非高斯、非线性问题/处理

发展现状：针对三非（非平稳、非高斯、非线性）问题，先后发展出了相应的理论与方法。

非平稳：各种时频分析理论与方法（小波分析、分数阶傅氏变换）、循环平稳理论与方法；

非高斯：高阶统计分析理论与方法（高阶累积量、高阶谱）；

非线性：EKF、UKF、PF等。

七. 参考书籍

1.羊彦，景占荣，高田. 信号检测与估计. 西北工业大学出版社，2014

2. 段凤增. 信号检测与估计. 哈尔滨工业大学出版社，2002

3. 李道本. 信号的统计检测与估计理论. 科学出版社，2004

4. 叶中付. 统计信号处理. 中国科学技术大学出版社，2009

5. 史蒂文 M 凯. 统计信号处理基础—估计与检测理论. 电子工业出版社，2003

关注

2
点赞
踩
2

收藏

觉得还不错? 一键收藏
打赏
0
评论
详解信号的参数估计

一. 估计的评价准则假设a是一个广义平稳随机信号x(n)的一个特征量，代表a的一个估计量。估计的偏差可以反应估计量与真值的接近程度，定义如下：直观上，B越小，对a的估计就越好。理论上当样本数N趋于无穷大时，会形成逐渐无偏估计，如下：估计的方差可以表示各次估计值相对估计均值的分散程度。估计的方差定义如下：估计的均方误差可以综合反映估计的特性，定义如下：如果均方误差满足如下条件，则称其为一致估计，如下：样本数二. 一致估计给定一致估计，证明偏差和方差都趋..
复制链接

扫一扫

专栏目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

唠嗑！ 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。