【随机信号处理笔记】 Chapter6 信号估计

6.1 估计模型

估计：当信号肯定存在时根据测量值和某种准则确定信号的数量特征的过程称为估计

参量估计：

• 最大似然估计
• 最大后验概率估计
• 贝叶斯估计
• 最小二乘估计
• 线性最小均方误差估计
• 线性递推估计

波形估计

• 线性最小均方误差估计
• 维纳滤波器
• 卡尔曼滤波器

6.2 最大似然估计（ML）

观测样本：$x_i=\theta +n_i$其中$\theta$为被估参量

似然函数：N次观测后，$\theta$出现时，x的条件密度函数

最大似然方程：$\frac{\partial f(X/\theta )}{\partial \theta }=0\theta ={\theta }^{\ast }={\hat{\theta }}_{ML}$

• 没有利用先验知识，性能比贝叶斯估计差
• 适用与$\theta$为未知非随机参量、为随机参量但先验概率未知、为计算后验概率难于计算似然函数
• 当观察数据足够多时，性能最优

6.3 最大后验概率估计（MAP）

观测样本：$x_i=\theta +n_i$

单样本后验概率：$P(\theta /x_i)$

样本矢量后验概率：N次观测后：$P(\theta /X)=\frac{P(\theta )f(X/\theta )}{f(X)}$

最大后验估计方程：$\frac{\partial P(\theta /X)}{\partial \theta }=0\theta ={\theta }^{\ast }={\hat{\theta }}_{MAP}$

• 先验概率$P(\theta )$为均匀分布时，MAP等价于ML

6.4 贝叶斯估计

估计误差：$\tilde{\theta }=\theta -\hat{\theta }(X)$真实值-估计值（多次估计）

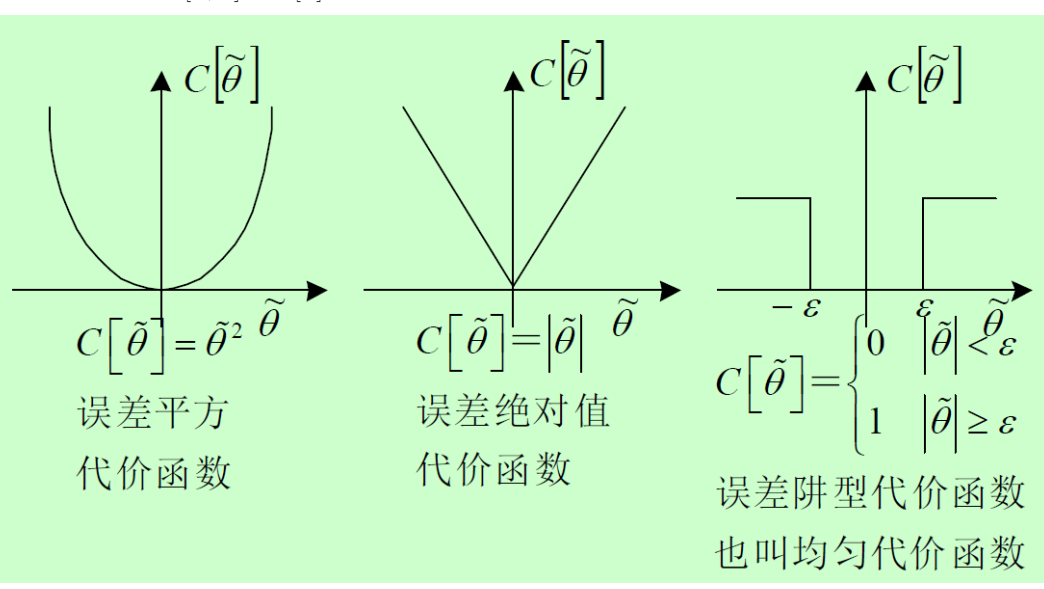
损失代价函数：$C[\theta ,\hat{\theta }]或C[\tilde{\theta }]\ge 0$

观测与估计的联合密度函数：

$f(X,\bar{\theta })=f(X/\bar{\theta })\text{似然函数 }p(\bar{\theta })\text{先验概率}=f(\bar{\theta }/X)\text{后验概率 }f(X)$

条件风险：$R(\overline{\bar{\theta }}/X)=\int C(\bar{\theta },\overline{\bar{\theta }})f(\bar{\theta }/X)d\bar{\theta }$，观测后多次x的风险，代价*后验积分

平均风险：$R(\overline{\bar{\theta }})=E[R(\bar{\theta }/X)]=\iint C[\bar{\theta },\bar{\theta }]f(X,\bar{\theta })d\bar{\theta }dX$对所有多次观测求平均

贝叶斯估计：平均风险最小$\frac{\partial }{\partial \hat{\bar{\theta }}}R(\overline{\bar{\theta }}/X)=0$

$\min R(\overline{\bar{\theta }})=\min R(\overline{\bar{\theta }}/X)$对于给定X，风险与条件风险相同

平方误差代价函数下的贝叶斯估计

条件风险：$R(\hat{\theta }/X)={\int }_{-\infty }^{\infty }(\theta -\hat{\theta }{)}^{2}f(\theta /X)d\theta$

对估计量求导：$2\hat{\theta }{\int }_{-\infty }^{\infty }f(\theta /X)d\theta -2{\int }_{-\infty }^{\infty }\theta f(\theta /X)d\theta =0$，其中第一项积分为1

解得贝叶斯估计量：${\hat{\theta }}_{MS}(X)={\int }_{-\infty }^{\infty }\theta f(\theta /X)d\theta =E[\theta /X]$

• 贝叶斯估计量=给定X下$\theta$的条件均值、后验均值
• 风险=均方误差
• 平方误差代价函数下的贝叶斯估计又称最小均方误差估计

绝对误差代价函数下的贝叶斯估计

条件风险：$R(\hat{\theta }/X)={\int }_{-\infty }^{\infty }|\theta -\hat{\theta }|f(\theta /X)d\theta$

贝叶斯估计量：后验概率密度中值

• 绝对误差代价函数下的贝叶斯估计又称条件中值估计

阱型误差代价函数下的贝叶斯估计

条件风险：$R(\hat{\theta }/X)={\int }_{-\infty }^{\hat{\theta }-\epsilon }f(\theta /X)d\theta +{\int }_{\hat{\theta }+\epsilon }^{\infty }f(\theta /X)d\theta$

贝叶斯估计量：后验概率密度众数，即最大后验概率

• 阱型误差代价函数下的贝叶斯估计又称MAP估计

贝叶斯估计量的不变性

约束条件1：

• 代价函数y轴对称
• 代价函数下凸
• 后验概率密度对条件均值对称

约束条件2：

• 代价函数y轴对称
• 代价函数非减
• 后验概率密度对条件均值对称，且为单峰函数

以上两种条件下，最小均方误差、条件中值、MAP估计等价，为贝叶斯估计

估计量的无偏性

对于确知参量，保证估计均值相等即无偏

对于随机参量，保证估计均值与参量均值相等即无偏

$\begin{array}{rl}& E\left({\hat{\theta }}_N\right)=\theta ,\text{ 对于非随机参量 }\\ & E\left({\hat{\theta }}_N\right)=E(\theta ),\text{ 对于随机参量 }\end{array}$

均值的无偏无法保证实际每一次估计均为无偏

条件无偏估计：

非随机参量估计：$E\left\{{\hat{\theta }}_N\right\}=\int {\hat{\theta }}_N(X)f(X/\theta )dX=\theta$

估计*似然的积分为确知即无偏

随机参量估计：$E\left\{{\hat{\theta }}_N\right\}=\iint {\hat{\theta }}_N(X)f(X,\theta )dXd\theta =E(\theta )$

估计*似然的二重积分为实际均值即无偏

渐进无偏：

非随机：${\lim }_{N\to \infty }E\left\{{\hat{\theta }}_N\right\}=\theta$

随机：${\lim }_{N\to \infty }E\left\{{\hat{\theta }}_N\right\}=E(\theta )$

有偏估计：

非随机：估计偏差：$E\left\{{\hat{\theta }}_N\right\}-\theta =b_N(\theta )\ne 0$

随机：估计偏差：$E\left\{{\hat{\theta }}_N\right\}-E(\theta )=b_N(\theta )\ne 0$

估计一致性（N无穷，误差不可能大）

随观测次数增加，使得估计尽可能无偏（均方误差不断减小）

一致估计，数学表达为（其中$\epsilon$为任意小正数）：

非随机：${\lim }_{N\to \infty }P\left\{\left|{\hat{\theta }}_N-\theta \right|>\epsilon \right\}=0$

随机：${\lim }_{N\to \infty }P\left\{\left|{\hat{\theta }}_N-E(\theta )\right|>\epsilon \right\}=0$

无条件一致估计：${\lim }_{N\to \infty }P\left\{\left|E\left({\hat{\theta }}_N\right)-\theta \right|>\epsilon \right\}=0$

均方一致估计：${\lim }_{N\to \infty }E\left[{\left({\hat{\theta }}_N-\theta \right)}^2\right]=0$

估计有效性

相对概念，估计的均方误差越小，估计越有效，当估计满足克拉美-罗不等式的等号时，估计为最小均方误差估计

6.5 最小二乘估计

最小二乘估计不需要统计前提知识

观测式：$x_i=\theta +n_i$

估计量：$\theta$估计为$\hat{\theta }$

！测量误差：${\tilde{\theta }}_i=x_i-\hat{\theta }$

误差平方和：$J(\tilde{\theta })={\sum }_{i=1}^N{\tilde{\theta }}_i^2={\sum }_{i=1}^N{\left(x_i-\hat{\theta }\right)}^2$

最小二乘估计就是要使得误差平方和最小，有${\hat{\theta }}_{LS}=\frac{1}{N}{\sum }_{i=1}^N{x}_i$

高斯噪声下，最大似然估计等价于最小二乘估计

估计的比较：

6.6 正交原理与波形估计

正交原理：若$E[\hat{\theta }\tilde{\theta }]=0$则称估计量$\hat{\theta }$与估计误差$\tilde{\theta }$正交，正交原理相当于参量估计里解析法要求的偏导为0

波形估计：根据已知$x(t)$

• 使用滤波器估计$s(t)$
• 预测$s(t+\tau )$
• 平滑$s(t-\tau )$

波形的线性最小均方误差估计

估计量： y ^ ( t ) = L { x ( ξ ) : ξ ∈ I } , x ( ξ )  的线性组合。  \hat{y}(t)=L\{x(\xi): \xi \in I\}, x(\xi) \text { 的线性组合。 } y^​(t)=L{x(ξ):ξ∈I},x(ξ) 的线性组合。 

估计误差：$\tilde{y}(t)=y(t)-\hat{y}(t)$

均方误差：$E\left[\tilde{y}(t{)}^2\right]=E\left[(y(t)-\hat{y}(t){)}^2\right]$

最小均方误差条件：$E\left[\tilde{y}(t)x\left({\xi }_i\right)\right]=0$ //测量和估计误差正交

相关性：$R_{xy}(\tau )=E[x(t)y(t+\tau )]$

• 随着时间间隔增大，自相关降低，均方误差增大
• 估计性能取决于相关函数
• 对于高斯噪声这种无相关性的随机过程，无法估计

6.7 维纳滤波器

维纳滤波器基本思想：寻求线性滤波器最佳传递函数，使得输出波形为作为输入波形的估计时的均方误差达到最小
使得：$\min \left\{E\left[\tilde{y}(t{)}^2\right]\right\}=\min \left\{E[y(t)-x(t)\otimes h(t){]}^2\right\}$

求$h(t)$

同样使用正交原理，得到

当$R_{yx}(\tau )={\int }_{t-b}^{t-a}{R}_{xx}(\tau -\lambda )h(\lambda )d\lambda$时，均方误差最小

积分上下限取0和正无穷时，称为维纳霍夫方程，系统传递函数在小于0时为0，为因果系统

分析非因果系统维纳滤波器可以帮助分析因果系统，非因果下易于计算

对于非因果系统：

$H(\omega )=\frac{S_{yx}(\omega )}{S_{xx}(\omega )}=\frac{S_{ss}(\omega )}{S_{ss}(\omega )+S_{nn}(\omega )}$

噪声的自功率谱密度在小频段被滤波器放大，较大频段被滤波器抑制

6.8 卡尔曼滤波器

适用条件：离散线性滤波问题

优势：

• 数据存储量小
• 递推算法易于实现
• 可推广至非平稳随机过程

信号模型：

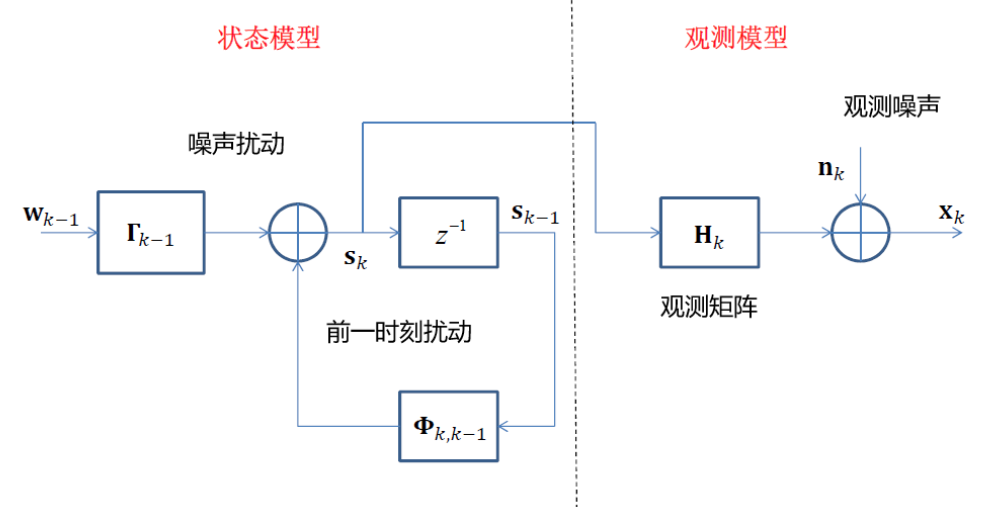
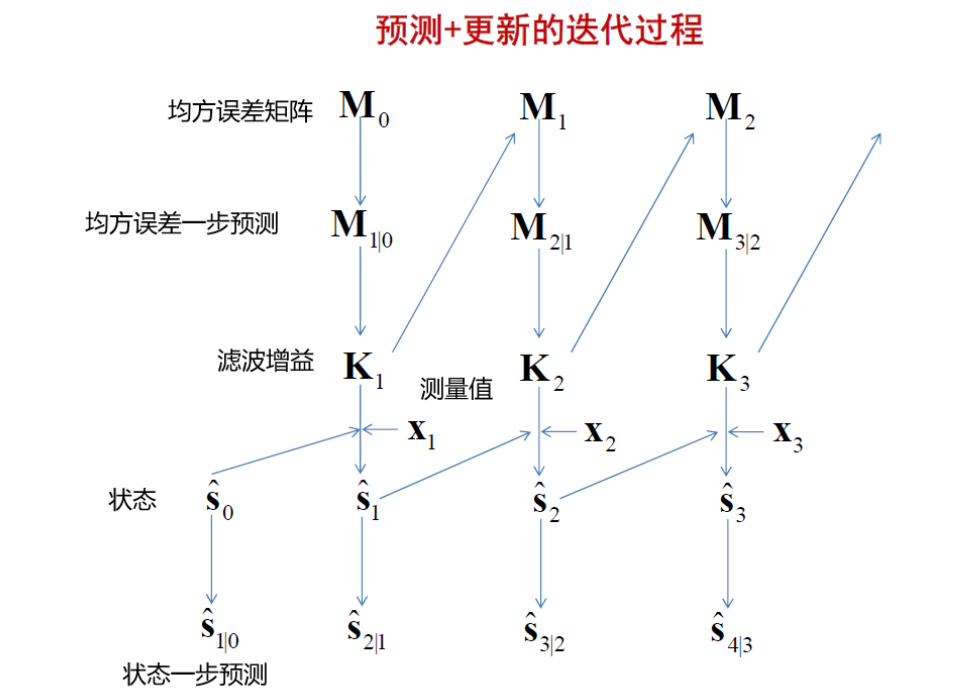
卡尔曼滤波递推流程：

1. 使用均方误差矩阵更新均方误差一步预测
2. 由均方误差一步预测计算滤波增益
3. 使用滤波增益更新均方误差矩阵
4. 根据上一步状态、滤波增益、实际测量更新状态
5. 更新状态一步预测