Danskin's theorem
From Wikipedia, the free encyclopedia
In convex analysis, Danskin's theorem is a theorem which provides information about the derivatives of a function of the form
The theorem has applications in optimization, where it sometimes is used to solve minimax problems.
[edit]Statement
The theorem applies to the following situation. Suppose  is a continuous function of two arguments,
is a continuous function of two arguments,
where  is a compact set. Further assume that
is a compact set. Further assume that  is convex in
is convex in  for every
for every  .
.
Under these conditions, Danskin's theorem provides conclusions regarding the differentiability of the function
To state these results, we define the set of maximizing points  as
as
Danskin's theorem then provides the following results.
-
Convexity
-
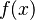 is
convex.
Directional derivatives
is
convex.
Directional derivatives
-
The
directional derivative of
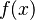 in the direction
in the direction
 , denoted
, denoted
 , is given by
, is given by
-
-
where
 is the directional derivative of the function
is the directional derivative of the function
 at
at
 in the direction
in the direction
 .
Derivative
.
Derivative
-
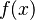 is
differentiable at
is
differentiable at
 if
if
 consists of a single element
consists of a single element
 . In this case, the
derivative of
. In this case, the
derivative of
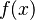 (or the
gradient of
(or the
gradient of
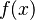 if
if
 is a vector) is given by
is a vector) is given by
-
-
Subdifferential
-
If
 is differentiable with respect to
is differentiable with respect to
 for all
for all
 , and if
, and if
 is continuous with respect to
is continuous with respect to
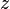 for all
for all
 , then the
subdifferential of
, then the
subdifferential of
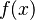 is given by
is given by
-
-
where
 indicates the
convex hull operation.
indicates the
convex hull operation.
[edit]References
- Bertsekas, Dimitri P. (1999). Nonlinear Programming. Belmont, MA: Athena Scientific. pp. 717. ISBN 1-886529-00-0.



























 1372
1372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








