立体像对前方交会模型

前言

用两张相互重叠的相片构建三维基底是立体摄影测量的基础，同样也是视觉三维重建的基础。这样的原理很容易的扩展为由一系列像对构建的摄影测量网中。用单像空间后方交会模型来求地面点的空间坐标是不可能的，仅仅通过一个已知像点只能确定该相片的空间方位以及摄影中心至像点的射线空间方向，只有利用同一个像点的立体像对，才能得到两条同名射线在空间相交的点，即该地面点的空间位置。

模型的数学表达

立体像对与所摄影地面点存在的几何关系，如下图所示：

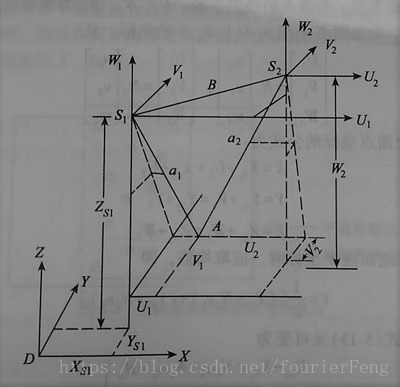
为了接下来构造解算模型，首先需要用数学表达式来描述这个几何关系，若在$S_{1}$、$S_{2}$两个方位通过相机对地面拍照，来获取一个立体像对，假设对一个地面特征点$A$,在像对的左右相片的构像为$a_{1}$、$a_{2}$，显然，两条射线$S_{1}a_{1}$，$S_{2}a_{2}$交于$A$。如上图所示，人为规定$D-XYZ$为世界坐标系，为了利用相机内参不变的特性以完成参数拟合，地面特征点及其对应的像点应该以相机为基准进行分析，所以还需要建立两个像空间辅助坐标系：$S_{1}-U_{1}V_{1}W_{1}$、$S_{2}-U_{2}V_{2}W_{2}$两个坐标系的原点在相机的位置，为了和世界坐标系更方便的交互，可设置为三个坐标轴对应的平行，即互为平移关系。这里继续设$A$点在两个像空间辅助坐标系的坐标分别为：$(U_{1},V_{1},W_{1})$、$(U_{2},V_{2},W_{2})$，$A$点对应的像点$a_{1}$、$a_{2}$的像空间坐标为$(x_{1},y_{1},-f)$、$(x_{2},y_{2},-f)$，对应的像空间辅助坐标为$(u_{1},v_{1},w_{1})$、$(u_{2},v_{2},w_{2})$，则可建立线性方程组：

$$\begin{bmatrix} u_{1}\\ v_{1}\\ w_{1} \end{bmatrix}=R_{1}\begin{bmatrix} x_{1}\\ y_{1}\\ -f \end{bmatrix},\begin{bmatrix} u_{2}\\ v_{2}\\ w_{2} \end{bmatrix}=R_{2}\begin{bmatrix} x_{2}\\ y_{2}\\ -f \end{bmatrix}$$
式中， $R_{1}$、 $R_{2}$为已经求得的左右像片的旋转矩阵。由于要求基线 $B$的三个分量$B_{u}$、 $B_{v}$、 $B_{w}$，需要求右摄影站点 $S_{2}$在 $S_{1}-U_{1}V_{1}W_{1}$中的坐标，由下式可得：
$$\left.\begin{matrix} B_{u}=X_{S_{2}}-X_{S_{1}}\\ B_{v}=Y_{S_{2}}-Y_{S_{1}}\\ B_{w}=Z_{S_{2}}-Z_{S_{1}} \end{matrix}\right\}$$
利用辅助坐标系与世界坐标系的平行关系，且相机光心、像点、物点三点共线，由此可得到：
$$\left.\begin{matrix} \frac{S_{1}A}{S_{1}a_{1}}=\frac{U_{1}}{u_{1}}=\frac{V_{1}}{v_{1}}=\frac{W_{1}}{w_{1}}=N_{1}\\ \frac{S_{2}A}{S_{2}a_{2}}=\frac{U_{2}}{u_{2}}=\frac{V_{2}}{v_{2}}=\frac{W_{2}}{w_{2}}=N_{2} \end{matrix}\right\}$$
式中， $U_{1}$、 $V_{1}$、 $W_{1}$为物点 $A$在$S_{1}-U_{1}V_{1}W_{1}$中的坐标； $U_{2}$、 $V_{2}$、 $W_{2}$为物点 $A$在$S_{2}-U_{2}V_{2}W_{2}$中的坐标。
由于
$$\left.\begin{matrix} X=X_{S_{1}}+U_{1}=X_{S_{2}}+U_{2}\\ Y=Y_{S_{1}}+V_{1}=Y_{S_{2}}+V_{2}\\ Z=Z_{S_{1}}+W_{1}=Z_{S_{2}}+W_{2} \end{matrix}\right\}$$
上式又可变为：
$$\left.\begin{matrix} X_{S_{2}}-X_{S_{1}}=N_{1}u_{1}-N_{2}u_{2}=B_{u}\\ Y_{S_{2}}-Y_{S_{1}}=N_{1}v_{1}-N_{2}v_{2}=B_{v}\\ Z_{S_{2}}-Z_{S_{1}}=N_{1}w_{1}-N_{2}w_{2}=B_{w} \end{matrix}\right\}$$
上式一、三两式联立，得投影系数得计算公式：
$$\left.\begin{matrix} N_{1}=\frac{B_{u}w_{2}-B_{w}u_{2}}{u_{1}w_{2}-u_{2}w_{1}}\\ N_{2}=\frac{B_{u}w_{1}-B_{w}u_{1}}{u_{1}w_{2}-u_{2}w_{1}} \end{matrix}\right\}$$
在具体计算时，取算术平均值的中误差要比观测值的中误差小（小 $\sqrt{n}$倍，其中 $n$是观测次数），所以在求地面点坐标时，取摄影站点的平均值：
$$\left.\begin{matrix} X=\frac{1}{2}\left [ (X_{S_{1}}+N_{1}u_{1})+(X_{S_{2}}+N_{2}u_{2}) \right ]\\ Y=\frac{1}{2}\left [ (Y_{S_{1}}+N_{1}v_{1})+(Y_{S_{2}}+N_{2}v_{2}) \right ]\\ Z=\frac{1}{2}\left [ (Z_{S_{1}}+N_{1}w_{1})+(Z_{S_{2}}+N_{2}w_{2}) \right ] \end{matrix}\right\}$$
这样就可以获得物点在世界坐标系中的坐标。当然如果仅仅是双工业相机，这个误差往往会很大，如果不考虑成本问题，多添加几个工业相机，则可以利用测量平差来减小误差。而且一般来讲量测物点坐标首先要做的是对每个目做 单像空间后方交会来计算六个外方位元素（ $X_{S}$、 $Y_{S}$、 $Z_{S}$、 $\varphi$、 $\omega$、 $\kappa$），所以在这一阶段提取特征点的个数和准确率也会直接影响到最终物点坐标的精确度。
下面是立体像对前方交会模型解算的简单代码，希望各位读者多提宝贵意见。

#ifndef SPACEINTERSECTION
#define SPACEINTERSECTION
#include "math.h"


inline void get_auxiliary_coordinate(double3 *auxiliary_coordinate_set, double9 matrix
, double2 *image_feature,double f)
{
    double3 image_feature_f;

    for (int i = 0; i != 2; ++i)
    {
        memcpy(image_feature_f, image_feature[i], sizeof(double)* 2);
        image_feature_f[2] = f;

        MultMatrix(matrix, image_feature_f, auxiliary_coordinate_set[i], 3, 3, 1);
    }
}

inline void get_baseline_weight(double3 B, double3 s1, double3 s2)
{
    B[0] = s2[0] - s1[0];
    B[1] = s2[1] - s1[1];
    B[2] = s2[2] - s1[2];
}

inline void get_projection_coefficient(double2 N, double3 *auxiliary_coordinate_set, double3 B)
{
    N[0] = (B[0] * auxiliary_coordinate_set[1][2] - B[2] * auxiliary_coordinate_set[1][0])
        / (auxiliary_coordinate_set[0][0] * auxiliary_coordinate_set[1][2] 
        - auxiliary_coordinate_set[1][0] * auxiliary_coordinate_set[0][2]);

    N[1] = (B[0] * auxiliary_coordinate_set[0][2] - B[2] * auxiliary_coordinate_set[0][0])
        / (auxiliary_coordinate_set[0][0] * auxiliary_coordinate_set[1][2] 
        - auxiliary_coordinate_set[1][0] * auxiliary_coordinate_set[0][2]);
}

inline void get_ground_coordinate(double3 groud_coordinate, double2 N
, double3 *auxiliary_coordinate_set, double3 s1, double3 s2)
{
    groud_coordinate[0] = 0.5*(s1[0] + N[0] * auxiliary_coordinate_set[0][0] 
        + s2[0] + N[1] * auxiliary_coordinate_set[1][0]);

    groud_coordinate[1] = 0.5*(s1[1] + N[0] * auxiliary_coordinate_set[0][1]
        + s2[1] + N[1] * auxiliary_coordinate_set[1][1]);

    groud_coordinate[2] = 0.5*(s1[2] + N[0] * auxiliary_coordinate_set[0][2]
        + s2[2] + N[1] * auxiliary_coordinate_set[1][2]);
}

#endif

当然，这只是“求”的过程，真正关键的还是内定向、相对定向、绝对定向。在下面的文章中将要继续讨论的。
参考文献：
[1] 摄影测量原理 王之卓编著
[2] 摄影测量学（测绘工程专业） 王佩军，徐亚明编著

转载请注明出处：https://blog.csdn.net/fourierFeng/article/details/80239502