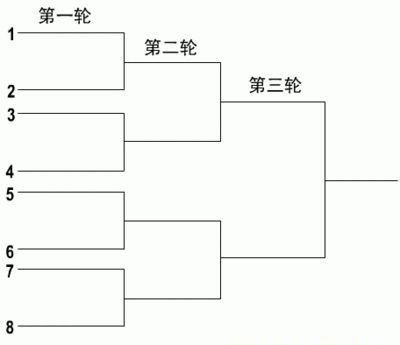
对于这种单循环赛制acm也是常遇到这样的题那么,对于这样的比赛我们要怎么模拟所有的可能是一个问题,我们如何判断两个队在某一轮是否会遇到呢
我们其实可以利用二进制的性质
设某一轮比赛为i,求j和k两只队伍是否能比赛,下面我们用二进制来表示队伍的队号
0001(1)
0010(2)
0011(3)
0100(4)
0101(5)
0110(6)
0111(7)
1000(8)
我们让所有的队伍先减1
得到
0000(1)
0001(2)
0010(3)
0011(4)
0100(5)
0101(6)
0110(7)
0111(8)
对于第i=1局比赛只能是相连的两支队伍进行比赛,我们观察一下发现1-2,3-4,5-6,7-8,他们除了最后一位,他们的前缀都同那么我们抹去最后的i-1位,即进行右左移操作(j-1)>>(i-1),对于最后一位来说相连不同的数只是相差1或0我们利用^异或操作可以使最后一位变为相等,(2n)^1=2n+1,(2n+1)^1=2n,如当j=4(100)时(j-1)^1=2与k=3,k-1相等
接下来第i=2局比赛,

那么当第i=3局比赛时

综上:判别条件是((j-1)>>(i-1))^1==((k-1)>>(i-1)
for(int i=1;i<=len;i++) dp[0][i]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=len;j++)
for(int k=1;k<=len;k++)
if((((j-1)>>(i-1))^1)==((k-1)>>(i-1)))























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








