LOF（Local Outlier Factor）：局部异常因子

局部异常因子LOF是一种异常检测方法，是属于基于邻近的方法中的一种。

基于邻近的方法大概分为三类，分别是：

聚类方法，如KNN；基于距离的方法；基于密度的方法；

局部异常因子LOF是属于第三类，即基于密度的方法中的一种。

 

局部异常因子算法（Local Outlier Factor）通过计算“局部可达密度”来反映一个样本的异常程度，一个样本点的局部可达密度越大，这个点就越有可能是异常点。

 

用通俗的话来讲就是：若点P的局部范围内，数据点的密度越小，则点P越有可能是异常点。

一、k距离邻域：表示K个数据点组成的一个邻域范围

　　某一点P的k距离（k-distance）很容易解释，就是点P和距离点P第k近的点之间距离，但不包括P。假设P是学校，葛小伦、刘闯、赵信、蔷薇、琪琳、炙心6个同学都住在学校附近：

　　图1

　　为了简单前起见，将P放置在原点。用欧几里得距离表示每个同学的家到学校的距离，由近及远分别是葛小伦<刘闯<赵信<蔷薇=炙心<琪琳，距P最近的是葛小伦，第2近的是刘闯，第3近的是赵信，第4近的是蔷薇和炙心，第5近的是琪琳。

　　当k=t时，在数据集中用下式表示x(i)的k距离，其中x(k=t)表示距x(i)第k远的数据样本：

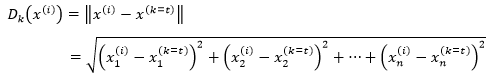
　　所谓P的k距离邻域（k-distance neighborhood of p），就是到P的直线距离小于P的k距离的所有数据样本构成的集合。

       在图1中，当k=3时，P的k距离邻域是{葛小伦、刘闯、赵信}；当k=4时，P的k距离邻域是{葛小伦、刘闯、蔷薇、炙心}。

　　可以把P看作圆心，把P的k距离看作半径做一个圆，圆中的样本点就是P的k距离邻域：

　　图2

二、可达距离：在点P的邻域范围内存在若干个点，距离点P距离最远的点A，则P的可达距离则为P与A之间的距离

　　x(i)到x(j)的可达距离（Rechabiliby Distance）可以表示为：

　　它的含义是，当x(i)距x(j)的距离比x(i)距x(k=t)更近时，直接用数值较大的|| x(i)- x(k=k)||表示x(i)到x(j)的可达距离，否则用|| x(i)- x(j)||表示。

　　以图1为例，当k=3时，距P第3近的同学是赵信，P的k距离邻域是{葛小伦、刘闯、赵信}，则P到他们的可达距离都等于学校到赵信家的距离；P到蔷薇、炙心、琪琳的可达距离与学校到她们的实际距离相等：

　　由于以x(i)的k近距离和x(j)的k距离并不相等，所以x(i)到x(j)的可达距离和x(j)到x(i)的可达距离并不相等：

　　图3

　　在图3中，当k=2时，先计算x(1)到x(2)的可达距离，此时距x(1)第2近的点是x(4)：

　　再来看看x(2)到x(1)的可达距离，距x(2)第2近的点是x(3)：

　　由此可见：

三、局部可达密度

　　点与点之间的密度很容易理解，点之间距离越远，密度越低；距离越近，密度越高。

       局部可达密度与总体密度类似，只不过是用k距离邻域计算的，所以称为“局部”。

　　假设x(i)的k距离邻域中有N个样本点，用xN表示，xN(t)表示xN中的第t个样本点，那么x(i)的局部可达密度（local reachability density）可以写成：

　　上式中x(i)的局部可达密度是x(i)的k距离邻域中所有样本点到x(i)的可达距离的平均值的倒数。

     代表xN中样本点的密集程度，密集程度越高，该值越小，它的倒数（x(i)的局部可达密度）的值越大，x(i)和xN越可能是同一簇，即越可能是正常点；

      反之，如果x(i)是异常数据，那么xN中的样本点到x(i)的可达距离将会取这些样本点到x(i)的直线距离，这个距离将远大于xN中样本点的k距离，最终导致较大，它的倒数（x(i)的局部可达密度）的值较小，x(i)和xN越不是同一簇，即越可能是异常点。

简单而言，

x(i)的局部可达密度越大，x(i)越靠近它邻域中的点，越可能是正常点；

x(i)的局部可达密度越小，x(i)越远离它邻域中的点，越可能是异常点。

四、局部异常因子

　　有了局部可达密度，就可以进一步定义局部异常因子（local outlier factor）：

　　上式的分子表示x(i)的k距离邻域中的所有样本点的局部可达密度的均值，分母是x(i)的局部可达密度。

       它实际上是通过比较x(i)的密度和其邻域的密度来判断x(i)是否是异常点；

x(i)的密度越低，局部可达密度LRDk(x(i))越小，局部异常因子LOFk(x(i))的值越大，x(i)越可能是异常点；

x(i)的密度越高，局部可达密度LRDk(x(i))越大，局部异常因子LOFk(x(i))的值越接近1或小于1，x(i)越可能是正常的样本点。

 

参考：异常检测(1)——局部异常因子算法