J01 ~ J10

最新推荐文章于 2025-04-26 23:01:23 发布
最新推荐文章于 2025-04-26 23:01:23 发布
阅读量617 收藏
点赞数
分类专栏： Java算法天梯 文章标签： 算法 java 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/fuyuanduan/article/details/129957011
版权
该文展示了Java中关于整型的位操作，包括打印32位二进制、左移、右移、取反等，并探讨了整型的表示范围。此外，文章还详细介绍了几种经典的排序算法实现，如选择排序、插入排序和冒泡排序。同时，讨论了如何优化范围求和查询以及随机函数的使用，包括概率分布的验证和调整概率的方法。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

【J01】

打印一个整形的32位信息；

	/**
	 *@description: 打印一个整形的所有32位信息。
	 *@author: YguangY
	 *@date: 2023/4/4  16:46
	 **/
	public static void print(int num) {
		for (int i = 31; i >= 0; i--) {
			System.out.print((num & (1 << i)) == 0 ? "0" : "1");
		}
		System.out.println();
	}

【测试左移后填充】：

[ test01 ]:

//数字1左移后是拿0进行填充的；

 	public static void main(String[] args) {
		int test = 1;
		print(test);
		print(test<<1);     //跑过去之后是拿0填充的
		print(test<<2);
		print(test<<8);
	}

【输出】：
在这里插入图片描述

[ test02 ]:

 	public static void main(String[] args) {
		int test = 111111;
		print(test);
		print(test<<1);     //跑过去之后是拿0填充的
		print(test<<2);
		print(test<<8);
	}

//发现———是整体一坨坨移动的。
【输出】：
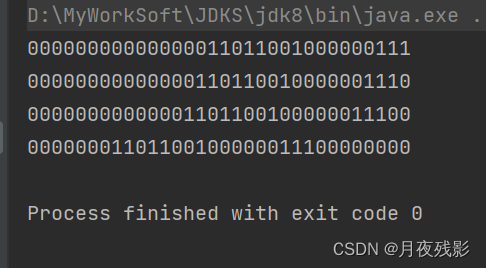
在这里插入图片描述

【test03】：

		int a = Integer.MAX_VALUE;
		System.out.println(a);
		print(a);

在这里插入图片描述
【发现】：
一个32位整型在系统中，不是全部位数都被占用的！！！最左侧的部分是留着的，真正占用的是从右数的0~30共31个位置；

【test04】：

		print(-1);
		int a = Integer.MIN_VALUE;
		print(a);

在这里插入图片描述

【test05】：取反

		int b = 123823138;
		int c = ~b;
		print(b);
		print(c);

在这里插入图片描述

【test06】：右移

		int x = 1024;
		print(x);
		print(x >> 1);
		print(x >>> 1);

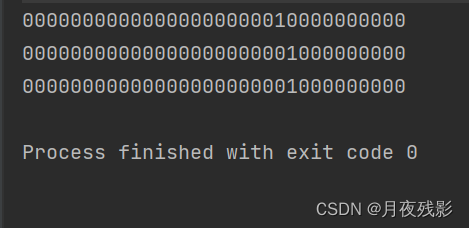
在这里插入图片描述

‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’‘’

		int a = Integer.MIN_VALUE;
		print(a);
		print(a >> 1);
		print(a >>> 1);

在这里插入图片描述

[test07]:

		int c = Integer.MIN_VALUE;
		int d = -c ;

		System.out.println( c );
		System.out.println( d );
		System.out.println("============================");
		
		print(c);
		print(d);

在这里插入图片描述
//最小的数取相反数还是它自己。

【J02】：

给定一个参数N ， 返回： 1！+2！+3！+4！+ … + N！ 的结果。

	/**
	 *@description:
	 *@author: YguangY
	 *@date: 2023/4/4 21:29
	 **/
	public static long f2(int N) {
		long ans = 0;
		long cur = 1;
		for (int i = 1; i <= N; i++) {
			cur = cur * i;
			ans += cur;
		}
		return ans;
	}

【J03】：

排序经典算法——选择排序；

	/**
	 *@description: 选择排序用到的交换方法；
	 *@author: YguangY
	 *@date: 2023/4/5 15:30
	 **/
	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[j];
		arr[j] = arr[i];
		arr[i] = tmp;
	}

	/**
	 *@description: 选择排序
	 *@author: YguangY
	 *@date: 2023/4/5 15:30
	 **/
	public static void selectSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		for (int i = 0; i < N; i++) {
			int minValueIndex = i;
			for (int j = i + 1; j < N; j++) {
				minValueIndex = arr[j] < arr[minValueIndex] ? j : minValueIndex;
			}
			swap(arr, i, minValueIndex);
		}
	}

【J04】：

经典排序算法——冒泡排序；

	/**
	 *@description: 冒泡排序。
	 *@author: YguangY
	 *@date: 2023/4/5 15:56
	 **/
	public static void bubbleSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		for (int end = N - 1; end >= 0; end--) {
			for (int second = 1; second <= end; second++) {
				if (arr[second - 1] > arr[second]) {
					swap(arr, second - 1, second);
				}
			}
		}
	}

	/**
	 *@description: 排序用到的交换方法；
	 *@author: YguangY
	 *@date: 2023/4/5 15:30
	 **/
	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[j];
		arr[j] = arr[i];
		arr[i] = tmp;
	}

【J05】：

经典排序算法——插入排序；

	/**
	 *@description: 插入排序1
	 *@author: YguangY
	 *@date: 2023/4/5 16:49
	 **/
	public static void insertSort1(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		for (int end = 1; end < N; end++) {
			int newNumIndex = end;
			while (newNumIndex - 1 >= 0 && arr[newNumIndex - 1] > arr[newNumIndex]) { //左边有数（防止指针越界） && 左边的数比我大
				swap(arr, newNumIndex - 1, newNumIndex);
				newNumIndex--;
			}
		}
	}

	/**
	 *@description: 插入排序2————优化的算法
	 *@author: YguangY
	 *@date: 2023/4/5 16:49
	 **/
	public static void insertSort2(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		int N = arr.length;
		for (int end = 1; end < N; end++) {
			//pre是当前的数的前一个位置；
			//pre是新数的前一个位置；———新数一开始是在end位置上。
			for (int pre = end - 1; pre >= 0 && arr[pre] > arr[pre + 1]; pre--) {
				swap(arr, pre, pre + 1);
			}
		}
	}

【J06】：

函数sum( arr , L , R ) 的作用是求数组[L]位置到[R]位置元素的累加和。
在这里插入图片描述
请设计两种数据结构，以便令单次查询更加快捷，同时需要满足如下两种情景：
（1）：
低频率的查询场景；
（2）：
高频率的查询场景（上亿次）。

	public static class RangeSum1 {

		private int[] arr;

		public RangeSum1(int[] array) {
			arr = array;
		}

		public int rangeSum(int L, int R) {
			int sum = 0;
			for (int i = L; i <= R; i++) {
				sum += arr[i];
			}
			return sum;
		}

	}

	public static class RangeSum2 {

		private int[] preSum;

		public RangeSum2(int[] array) {
			int N = array.length;
			preSum = new int[N];
			preSum[0] = array[0];
			for (int i = 1; i < N; i++) {
				preSum[i] = preSum[i - 1] + array[i];
			}
		}

		public int rangeSum(int L, int R) {
			return L == 0 ? preSum[R] : preSum[R] - preSum[L - 1];
		}

	}

一种是维护一个矩阵（代码中的RangeSum1 是直接计算L~R，并没有维护矩阵，生成矩阵方法类似，在此不再赘述）；
一种是维护一个前缀和数组。

【J07】：研究随机函数

一些对Math.random() 函数的研究；

【test01】:研究概率

    public static void main(String[] args) {
        System.out.println("测试开始");
        // Math.random() -> double -> [0,1)

        int testTimes = 10000000;
        int count = 0;
        for (int i = 0; i < testTimes; i++) {
            if (Math.random() < 0.75) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
        System.out.println("=========");
    }

【输出】：
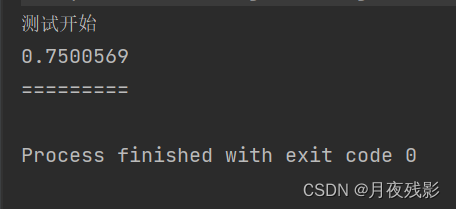
在这里插入图片描述
//概率的确非常精准。

【test02】：放缩后当然概率不变了

    public static void main(String[] args) {
        // [0,1) -> [0,8)
        //扩大之后，也是等概率返回的。

        int testTimes = 10000000;
        int count = 0;

        for (int i = 0; i < testTimes; i++) {
            if (Math.random() * 8 < 5) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
        System.out.println((double) 5 / (double) 8);
    }

在这里插入图片描述

【test03】：放缩后每一个数的概率测试

    public static void main(String[] args) {
        int testTimes = 10000000;

        int K = 10;
        // [0,K) -> [0,K-1]

        int[] counts = new int[K];
        for (int i = 0; i < testTimes; i++) {
            int ans = (int) (Math.random() * K); // [0,K-1]
            counts[ans]++;
        }
        for (int i = 0; i < K; i++) {
            System.out.println(i + "这个数，出现了 " + counts[i] + " 次");
        }

        System.out.println("=========");
    }

在这里插入图片描述
【修改K的值】：

  int K = 6;

在这里插入图片描述

【test04】：调整出现的概率为平方

[0,x]内的数出现的概率为x , 如何将x变为x的平方呢？

    public static void main(String[] args) {
        int testTimes = 10000000;
        int count = 0;

        double x = 0.17;
        for (int i = 0; i < testTimes; i++) {
            if (xToXPower2() < x) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
        System.out.println(Math.pow(x,2));
    }

    // 返回[0,1)的一个小数
    // 任意的x，x属于[0,1)，[0,x)范围上的数出现概率由原来的x调整成x平方
    public static double xToXPower2() {
        return Math.max(Math.random(), Math.random());
    }

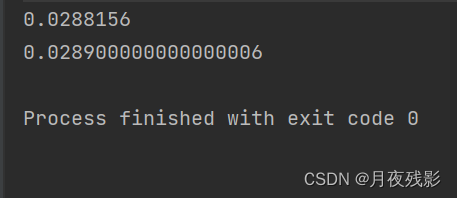
在这里插入图片描述

【test05】：调整出现的概率为三次方

[0,x]内的数出现的概率为x , 如何将x变为x的三次方呢？

    public static void main(String[] args) {
        int testTimes = 10000000;
        int count = 0;

        double x = 0.3;
        for (int i = 0; i < testTimes; i++) {
            if (xToXPower3() < x) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
        System.out.println(Math.pow(x,3));
    }

    // 返回[0,1)的一个小数
    // 任意的x，x属于[0,1)，[0,x)范围上的数出现概率由原来的x调整成x平方
    public static double xToXPower3() {
        return Math.max(Math.random(), Math.max( Math.random(),Math.random() ) );
    }

在这里插入图片描述

【test06】:使用min的话概率如何计算呢？

min ( 事件A ， 事件B )

=》

在这里插入图片描述
在这里插入图片描述

    public static void main(String[] args) {
        int testTimes = 10000000;
        int count = 0;

        double x = 0.2;
        for (int i = 0; i < testTimes; i++) {
            if (xToXPower3() < x) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
        System.out.println(1-Math.pow(1-x, 2));
    }

    // 返回[0,1)的一个小数
    // 任意的x，x属于[0,1)，[0,x)范围上的数出现概率由原来的x调整成x平方
    public static double xToXPower3() {
        return Math.min( Math.random() , Math.random() );
    }

在这里插入图片描述
1-（1-0.2）方 ==0.36.

【J08】：

条件函数F()等概率返回 1~5 ；
目标函数G（）要求等概率返回 1~7；

【test01】:测试零一发生器的概率

首先改造成零一发生器；

    public static void main(String[] args) {
        int testTimes = 10000000;
        int count = 0;

        for (int i = 0; i < testTimes; i++) {
            if (f2() == 0) {
                count++;
            }
        }
        System.out.println((double) count / (double) testTimes);
    }

    // lib里的，不能改！
    // 1~5 里等概率返回一个！！！
    public static int f1() {
        return (int) (Math.random() * 5) + 1;
    }

    // 随机机制，只能用f1，
    // 等概率返回0和1
    public static int f2() {
        int ans = 0;
        do {
            ans = f1();
        } while (ans == 3);     //f1得到的不是3 ， 才能从循环里出来；
        return ans < 3 ? 0 : 1;
    }

在这里插入图片描述
//说明零一发生器改造成功了；

【test02】: 0~7等概率返回

    // lib里的，不能改！
    // 1~5 里等概率返回一个！！！
    public static int f1() {
        return (int) (Math.random() * 5) + 1;
    }

    // 随机机制，只能用f1，
    // 等概率返回0和1
    public static int f2() {
        int ans = 0;
        do {
            ans = f1();
        } while (ans == 3);     //f1得到的不是3 ， 才能从循环里出来；
        return ans < 3 ? 0 : 1;
    }

    // 得到000 ~ 111 做到等概率 0 ~ 7等概率返回一个
    public static int f3() {
        return (f2() << 2) + (f2() << 1) + f2();
    }

    public static void main(String[] args) {
        int testTimes = 10000000;

        int[] counts = new int[8];
        for (int i = 0; i < testTimes; i++) {
            int num = f3();
            counts[num]++;
        }
        for (int i = 0; i < 8; i++) {
            System.out.println(i + "这个数，出现了 " + counts[i] + " 次");
        }
    }

在这里插入图片描述

【test03】:1~7等概率返回

    // lib里的，不能改！
    // 1~5 里等概率返回一个！！！
    public static int f1() {
        return (int) (Math.random() * 5) + 1;
    }

    // 随机机制，只能用f1，
    // 等概率返回0和1
    public static int f2() {
        int ans = 0;
        do {
            ans = f1();
        } while (ans == 3);     //f1得到的不是3 ， 才能从循环里出来；
        return ans < 3 ? 0 : 1;
    }

    // 得到000 ~ 111 做到等概率 0 ~ 7等概率返回一个
    public static int f3() {
        return (f2() << 2) + (f2() << 1) + f2();
    }

    // 0 ~ 6等概率返回一个
    public static int f4() {
        int ans = 0;
        do {
            ans = f3();
        } while (ans == 0);
        return ans;
    }

    public static int g() {
        return f4() ;
    }

    public static void main(String[] args) {
        int[] counts = new int[8];
        int testTimes = 10000000;

        for (int i = 0; i < testTimes; i++) {
            int num = g();
            counts[num]++;
        }
        for (int i = 0; i < 8; i++) {
            System.out.println(i + "这个数，出现了 " + counts[i] + " 次");
        }
    }

在这里插入图片描述

【test04】:

f（）函数是3~19上等概率随机的 ， 要求目标函数 g() 在20 ~ 56 上等概率随机；

    // 3~19 里等概率返回一个！！！
    public static int f1() {
        return (int) (Math.random() * 17) + 3;
    }

    // 等概率返回0和1
    public static int f2() {
        int ans = 0;
        do {
            ans = f1();
        } while (ans == 11);     //f1得到的不是11 ， 才能从循环里出来；
        return ans < 11 ? 0 : 1;
    }

    // 得到000000 ~ 111111 做到等概率 0 ~ 63等概率返回一个
    public static int f3() {
        return (f2()<<5 )+ (f2()<<4) + (f2()<<3) + (f2() << 2) + (f2() << 1) + f2();
    }

    // 20 ~ 56等概率返回一个
    public static int f4() {
        int ans = 0;
        do {
            ans = f3();
        } while (ans < 20 || ans > 56);
        return ans;
    }

    public static int g() {
        return f4() ;
    }

    public static void main(String[] args) {
            int[] counts = new int[100];
            int testTimes = 10000000;

            for (int i = 0; i < testTimes; i++) {
                int num = g();
                counts[num]++;
            }
            for (int i = 18; i < 60; i++) {
                System.out.println(i + "这个数，出现了 " + counts[i] + " 次");
            }
    }

在这里插入图片描述

【J09】：

f()函数得到0的概率是P ， 得到1的概率是（1-P） ， 即只返回0和1 ， 但是是不等概率的；
g()函数是目标函数，现在要求目标函数要等概率返回0和1；

    // 你只能知道，x会以固定概率返回0和1，但是x的内容，你看不到！
    public static int x() {
        return Math.random() < 0.84 ? 0 : 1;
    }

    // 等概率返回0和1
    public static int y() {
        int ans = 0;
        do {
            ans = x();
        } while (ans == x());  //在这个地方又调用了生成器！！！
        //即———第一次等于第二次的话，直接重做~ ~ ~ ！ ！ ！

        return ans;
    }

    public static void main(String[] args) {

        int[] arr = new int[10];

        for (int i = 0; i < 10000; i++) {
            int b =y();

            arr[b]++;
        }

        System.out.println(arr[0]);
        System.out.println(arr[1]);
        System.out.println(arr[2]);
        System.out.println(arr[3]);
    }

在这里插入图片描述

【J10】：

对数器；
//使用对数器验证——选择排序、插入排序是否正确。

  public static void selectionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            swap(arr, i, minIndex);
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

    public static void insertionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 1; i < arr.length; i++) { // 0 ~ i 做到有序
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j + 1);
            }
        }
    }

    /**
     * @description: 长度随机，内容随机的数组。
     * @author: YguangY
     * @date: 2023/4/7 10:23
     **/
    // 返回一个数组arr，arr长度[0,maxLen-1],arr中的每个值[0,maxValue-1]
    public static int[] lenRandomValueRandom(int maxLen, int maxValue) {
        int len = (int) (Math.random() * maxLen);
        int[] ans = new int[len];
        for (int i = 0; i < len; i++) {
            ans[i] = (int) (Math.random() * maxValue);
        }
        return ans;
    }

    public static int[] copyArray(int[] arr) {
        int[] ans = new int[arr.length];
        for (int i = 0; i < arr.length; i++) {
            ans[i] = arr[i];
        }
        return ans;
    }

    // arr1和arr2一定等长
    public static boolean isSorted(int[] arr) {
        if (arr.length < 2) {
            return true;
        }
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (max > arr[i]) {    //一直递增才是有序的！！！
                return false;
            }
            max = Math.max(max, arr[i]);
        }
        return true;
    }

    public static void main(String[] args) {
        int maxLen = 5;
        int maxValue = 1000;
        int testTime = 10000;
        for (int i = 0; i < testTime; i++) {
            int[] arr1 = lenRandomValueRandom(maxLen, maxValue);
            int[] tmp = copyArray(arr1);
            selectionSort(arr1);
            insertionSort(tmp);

            if (!isSorted(arr1)) {
                System.out.println("选择排序错了！");
                //也可以在此处进行BUG的定位~~~
            }

            if (!isSorted(tmp)) {
                System.out.println("插入排序错了");
                //也可以在此处进行BUG的定位~~~
            }
        }
    }
ZF均衡和ML均衡在不同天线数量下的MIMO系统误码率matlab仿真
平时工作较为繁忙,私信消息一般晚上回复,谢谢大家~~
01-22 839
前面学习了信道估计和插值，现在说说信道均衡，信道均衡的作用就是根据信道估计和插值的结果尽可能恢复发射数据。信道均衡技术主要有两种，迫零(ZF)均衡和最小均方误差(MMSE)均衡，实际上还有一个最大似然(ML)均衡，但计算量实在有点大。现在先说说ZF均衡。ZF均衡算法是一种根据峰值失真准则推导而来的线性均衡算法。将OFDM系统接收端的频域输出方程组用矩阵表示为Y=HX+W其中W为加性高斯白噪声。
golang 最短路径实现通过djistra,spfa,递归
热门推荐
小月肖的肖
05-07 1万+
{"graph":{"S263":{"J89": 40,"S271": 30},"J89":{"S263": 40,"BDBC1": 170,"BDB1": 100,"BD604": 280,"S267": 120},"S271":{"S263": 30,"BD01": 80},"S315":{"J40": 90,"S316": 10},"J40":{"S315": 90,"J39": 470,"...
【机组】基于FPGA的32位算术逻辑运算单元的设计（EP2C5扩充选配类）
朝花夕拾
01-26 1万+
本文深入探讨了基于FPGA的32位算术逻辑运算单元的设计，特别针对EP2C5扩充选配类进行了详细分析。作者在文章中详细介绍了设计过程，着重于FPGA在实现算术逻辑运算单元方面的优越性。通过EP2C5的扩充选配类，文章突显了设计的灵活性和适应性，使得该算术逻辑运算单元更加符合特定需求。此外，作者还对设计中的关键技术和实现细节进行了深入阐述，为读者提供了一个全面而深入的了解。该篇博文对于FPGA领域的研究者和开发人员具有重要的参考价值。
记录大正公式 转成总决算公式格式的过程
cris327的博客
07-15 194
历经数月，呕心连续之作，特此记录。
ML算法的matlab源码
FPGA/MATLAB学习教程/源码/项目合作开发
02-15 4306
clear N = 50000; % number of bits or symbols Eb_N0_dB = [0:20]; % multiple Eb/N0 values nTx = 2; nRx = 2; for ii = 1:length(Eb_N0_dB) % Transmitter ip = rand(1,N)>0.5; % generating 0,1 with equal probability s = 2*ip-1; % BPSK modulation 0 ...
oracle存储过程怎么做加密,Oracle 存储过程加密方法
weixin_34342091的博客
04-04 342
《Oracle 存储过程加密方法》由会员分享，可在线阅读，更多相关《Oracle 存储过程加密方法(3页珍藏版)》请在人人文库网上搜索。1、软件环境： 0W:J4L.m6j01、操作系统：Windows 2000 Server 建站之家-www.jz345.netEB1Od h0D2、数 据 库：Oracle 8i R2 (8.1.7) for NT 企业版 建站之家-www.jz345.netH...
CSS-Selector
feiyu5323的专栏
03-28 432
导航 (返回顶部) 1. CSS 1.1 CSS信息可以来自 1.2 采纳样式效果的优先级顺序为 2. Selectors 2.1 Selectors 适用于情况 2.2 Selectors 类型 3. Selectors List 4. See also 4.1 浏览器引擎支持对比 4.2 RWD响应式网页设计 4.3 CSS框架列表及对比 4.4 Bootstr...
【信号检测】MIMO ML-ZF-MMSES数字信号检测（BPSK调制 瑞利衰落信道 2个发送端 2个接收端）【含Matlab源码 4338期】
订阅付费专栏Matlab（奶茶价版）或下载付费资源，可赠送奶茶价版付费专栏指定代码1份；
04-23 1353
MIMO ML-ZF-MMSES数字信号检测（BPSK调制 瑞利衰落信道 2个发送端 2个接收端） 完整的代码，方可运行；可提供运行操作视频！适合小白！
【信号检测】基于matlab MIMO ML-ZF-MMSES数字信号检测（BPSK调制 瑞利衰落信道 2个发送端 2个接收端）【含Matlab源码 4338期】
订阅付费专栏Matlab（奶茶价版），可赠送奶茶价版付费专栏指定代码1份；
04-23 841
MIMO ML-ZF-MMSES数字信号检测（BPSK调制 瑞利衰落信道 2个发送端 2个接收端） 完整的代码，方可运行；可提供运行操作视频！适合小白！
超实用illustrator脚本AI脚本
08-02
J01-分割文本框架.js J02-添加当前色的 J03-用CMYK查找近似潘通色.js J04-建立点到点的连线.js J05-按数值选择路径对象.js J06-选择重叠的相同文本.js J07-随机填充色、轮 J08-弧形修正.js J08-虚线拐角补全.js J08-...
oracle创建表空间的sql
10-30
'D:\oracle\oradata\oemrep\j10.dbf' size18000M; ``` - **表空间名称**：“ռ”（这里似乎是个误输入的字符，请确保使用合适的名称）。 - **LOGGING**：表示此表空间支持事务日志记录，这对于需要恢复的表空间至关...
DW-J00/01无线开关量控制器技术详解
DW-J01型号的最大发射功率为500mw，通信距离在可视环境下可超过2700米，而DW-J00的发射功率为100mw。 该控制器设计有8路开关量输入和8路开关量输出，能够与DW-J10/11（支持16路输入）或DW-J20/21（支持16路输出）等...
Illustrator实用脚本集：文本、路径、颜色处理技巧
- **按锚点分隔路径（J10）**、**计算路径长度（J10）**、**删除所选锚点（J10）**：锚点是路径控制的关键点，这个脚本群可以帮助设计师更精细地调整路径，包括路径分隔、长度计算和锚点的删除。 - **尖角圆角化...
蓝桥杯 19.合根植物
wuqingshun314159的博客
04-22 436
如果我们告诉你哪些小格子之间出现了合根现象，你能计算出这个园中一共有多少株合根植物吗？输出一个整数，表示最后园中合根植物的数量。每个格子里种了一株合根植物。，从而与另一个格子的植物合成为一体。这种植物有个特点，它的根可能会沿着。这个是非常简单纯粹的并查集题目。W 星球的一个种植园被分成。
[Java · 铢积寸累] 数据结构 — 数组类型 - 增 & 删 & 改 & 查
Blue17 の 小窝
04-22 602
想系统化学习 Java 编程？在上一章中我们介绍了如何声明与创建数组，还介绍了数组的基本使用方式。本章我们将在上一章的基础上，拓展数组的使用方式（可能会涉及一些思维题）。
【力扣刷题实战】找到字符串中所有字母异位词
knowledge_Cheese的博客
04-22 1095
这里的emplace_back 函数 是 std::vector 容器提供的成员函数。它的作用是在 vector 的尾部直接构造新元素，而不是像 push_back 那样先创建一个临时对象，再将其拷贝或移动到 vector 尾部。的 ASCII 值映射到 0 到 25 的索引范围，所以使用长度为 26 的向量来存储每个字母的计数。的异位词的起始索引。异位词指的是由相同字母重排列形成的字符串（包括相同的字符串）。中字符的频率，找出所有异位词的起始位置。如果相等，说明字符串。的函数，它的主要功能是在字符串。
代码随想录算法训练营Day31 | 56. 合并区间 738.单调递增的数字
最新发布
m0_74154872的博客
04-26 102
一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。表示若干个区间的集合，其中单个区间为。请你合并所有重叠的区间，并返回。当且仅当每个相邻位数上的数字。的最大数字，且数字呈。时，我们称这个整数是。
算法之动态规划
qq_68194402的博客
04-21 1383
动态规划（Dynamic Programming, DP）是一种解决复杂问题的算法设计技术，适用于具有“重叠子问题”和“最优子结构”性质的问题。动态规划将问题分解成更小的子问题，通过解决这些子问题来解决原始问题。这种方法的关键在于避免重复计算。一旦解决了一个子问题，它的解就被存储起来，以便后续需要时直接使用，从而避免了重复计算。这种记忆化的技术称为“缓存”。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值