数据集蒸馏论文(三)：Dataset condensation with gradient matching

Dataset condensation with gradient matching

论文：Dataset condensation with gradient matching
代码：VICO-UoE/DatasetCondensation

摘要

• 特点：跨模型
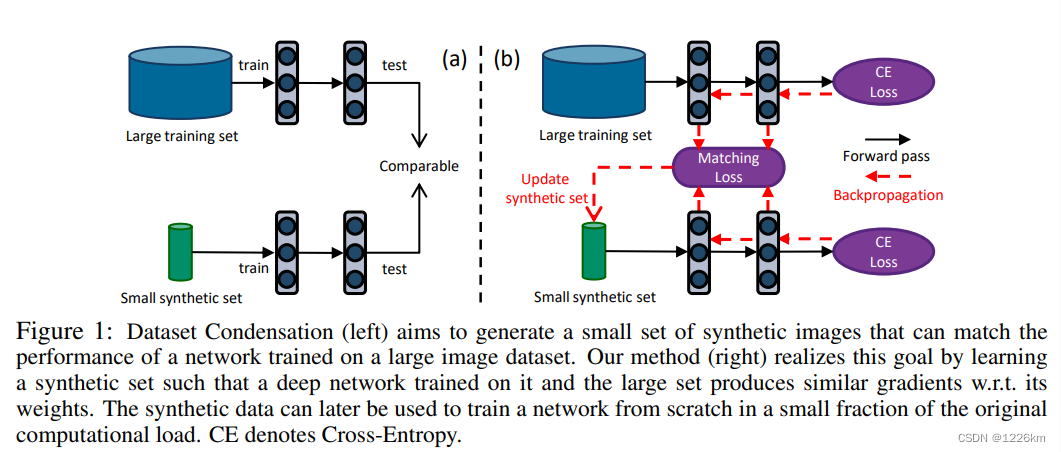
• 目的：将大型数据集压缩成一小部分信息丰富的合成样本，用于从头开始训练深度神经网络
• 目标函数：在原始数据上训练的深度神经网络权重的梯度与合成数据之间的梯度匹配问题
• 基于训练损失计算梯度
  

方法

2.1 Dataset condensation

• 原始训练数据集$|\mathcal{T}|$，由图像及其类标签对组成：
  $$\mathcal{T}=\{(x_i,y_i)\}{|}_{i=1}^{|\mathcal{T}|}$$其中，
  $x\in \mathcal{X}\subset {\mathbb{R}}^d$， y ∈ { 0 , . . . , C − 1 } y{\in}\{0,...,C-1\} y∈{0,...,C−1}；
  $\mathcal{X}$是一个$d$维输入空间；
  $C$是类别数量。

• 本文希望学习一个带有参数$\theta$的可微函数$\varphi$（如深度神经网络），以正确预测未知图像的标签，例如：$y-{\varphi }_{\theta }(x)$。

• 可以通过最小化训练集中的经验损失项来学习此函数的参数：
  $${\theta }^{\mathcal{T}}=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{T}}(\theta )\text{\hspace{1em}(1)}$$其中，
  ${\mathcal{L}}^{\mathcal{T}}(\theta )=\frac{1}{|\mathcal{T}|}{\sum }_{x,y\in \mathcal{T}}\ell ({\varphi }_{\theta }(x),y)$；
  $\ell (\cdot ,\cdot )$是特定任务损失（即交叉熵）；
  ${\theta }^{\mathcal{T}}$是${\mathcal{L}}^{\mathcal{T}}$的最小化。

• 所得模型${\varphi }_{{\theta }^{\mathcal{T}}}$的泛化性能可以写作${\mathbb{E}}_{x\in P_D}[\ell ({\varphi }_{{\theta }^T}(x),y)]$，其中$P_D$为数据分布。

• 合成数据集$|\mathcal{S}|$：
  $$\mathcal{S}=\{(s_i,y_i)\}{|}_{i=1}^{|\mathcal{S}|}$$其中，$s\in {\mathbb{R}}^d,y\in \mathcal{Y},|\mathcal{S}|\ll |\mathcal{T}|$。

• 类似于式(1)，学习合成数据集后，可以在其上训练$\varphi$：
  $${\theta }^{\mathcal{S}}=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{S}}(\theta )\text{\hspace{1em}(2)}$$其中，
  ${\mathcal{L}}^{\mathcal{S}}(\theta )=\frac{1}{|\mathcal{S}|}{\sum }_{x,y\in \mathcal{S}}\ell ({\varphi }_{\theta }(s),y)$；
  ${\theta }^{\mathcal{S}}$是${\mathcal{L}}^{\mathcal{S}}$的最小化。

• 由于合成集$|\mathcal{S}|\ll |\mathcal{T}|$，本文期望：
  式(2)中的优化明显快于式(1)；
  ${\varphi }_{{\theta }^{\mathcal{S}}}$的泛化性能接近${\varphi }_{{\theta }^{\mathcal{T}}}$，即在真实数据分布$P_D$下${\mathbb{E}}_{x\in P_D}[\ell ({\varphi }_{{\theta }^T}(x),y)]\backsimeq {\mathbb{E}}_{x\in P_D}[\ell ({\varphi }_{{\theta }^{\mathcal{S}}}(x),y)]$ 。

• 其他方法讨论
  在（Wang et al.，2018）中提出并在（Suchulutsky&Schonlau，2019；Bohdal et al.，2020；Such et al.，2020）中扩展，

    Tongzhou Wang, Jun-Yan Zhu, Antonio Torralba, and Alexei A Efros. Dataset distillation. arXiv preprint arXiv:1811.10959, 2018.
    Felipe Petroski Such, Aditya Rawal, Joel Lehman, Kenneth O Stanley, and Jeff Clune. Generative teaching networks: Accelerating neural architecture search by learning to generate synthetic training data. International Conference on Machine Learning, 2020.
    Ondrej Bohdal, Yongxin Yang, and Timothy Hospedales. Flexible dataset distillation: Learn labels instead of images. Neural Information Processing Systems Workshop, 2020.
    Ilia Sucholutsky and Matthias Schonlau. Soft-label dataset distillation and text dataset distillation. arXiv preprint arXiv:1910.02551, 2019.
  

  将参数${\theta }^{\mathcal{S}}$作为合成数据$\mathcal{S}$的函数：
  $${\mathcal{S}}^{\ast }=\arg \underset{\mathcal{S}}{\min }{\mathcal{L}}^{\mathcal{T}}({\theta }^{\mathcal{S}}(\mathcal{S}))\mathsf{subject}\mathsf{to}{\theta }^{\mathcal{S}}(\mathcal{S})=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{S}}(\theta )\text{\hspace{1em}(3)}$$
  该方法旨在找到合成图像的最佳集合${\mathcal{S}}^{\ast }$，以便在它们上训练的模型${\varphi }_{{\theta }^{\mathcal{S}}}$最小化原始数据的训练损失。
  优化等式(3)涉及嵌套循环优化和在每次迭代中解决${\theta }^{\mathcal{S}}(\mathcal{S})$的内部循环以恢复$\mathcal{S}$的梯度，这需要一个计算昂贵的过程——在$\theta$的多个优化步骤上展开$\mathcal{S}$的递归计算图（见（Samuel&Tappen，2009；Domke，2012））。
  因此，它不能扩展到大型模型或具有许多步骤的精确内环优化器。

    Kegan GG Samuel and Marshall F Tappen. Learning optimized map estimates in continuouslyvalued mrf models. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pp. 477–484. IEEE, 2009.
    Justin Domke. Generic methods for optimization-based modeling. In Artificial Intelligence and Statistics, pp. 318–326, 2012.
  

• 所以，本文提出了数据集压缩的替代公式。

2.2 具有参数匹配的Dataset condensation

• 本文目标是学习 $\mathcal{S}$ ，使其上训练的模型 ${\varphi }_{{\theta }^{\mathcal{S}}}$ 泛化性能与 ${\varphi }_{{\theta }^{\mathcal{T}}}$ 相当，且在参数空间中收敛到相似解（即 ${\theta }^{\mathcal{S}}\approx {\theta }^{\mathcal{T}}$）。

• 假设${\varphi }_{\theta }$是一个局部平滑函数，相似的权重$（{\theta }^{\mathcal{S}}\approx {\theta }^{\mathcal{T}}$）表示局部邻域中相似的映射，从而泛化性能，即${\mathbb{E}}_{x\in P_D}[\ell ({\varphi }_{{\theta }^T}(x),y)]\backsimeq {\mathbb{E}}_{x\in P_D}[\ell ({\varphi }_{{\theta }^S}(x),y)]$。

    局部平滑函数：Local smoothness is frequently used to obtain explicit first-order local approximations in deep networks(e.g. see (Rifai et al., 2012; Goodfellow et al., 2014b; Koh & Liang, 2017))
  

• 现在，可以将这个目标表述为：
  $$\underset{\mathcal{S}}{\min }D({\theta }^{\mathcal{S}},{\theta }^{\mathcal{T}})\mathsf{subject}\mathsf{to}{\theta }^{\mathcal{S}}(\mathcal{S})=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{S}}(\theta )\text{\hspace{1em}(4)}$$其中，
  ${\theta }^{\mathcal{T}}=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{T}}(\theta )$，
  $D(\cdot ,\cdot )$是距离函数。

• 在深度神经网络中，${\theta }^{\mathcal{T}}$通常取决于其初始值${\theta }_0$。

• 然而，式(4)中的优化旨在仅为初始化为${\theta }_0$的一个模型 ${\varphi }_{{\theta }^{\mathcal{T}}}$ 获得一组最佳合成图像，而我们的实际目标是生成可以处理随机初始化$P_{{\theta }_0}$分布的样本。

• 因此，本文修改式(4)如下：
  $$\underset{\mathcal{S}}{\min }{E}_{{\theta }_0\sim P_{{\theta }_0}}D({\theta }^{\mathcal{S}}({\theta }_0),{\theta }^{\mathcal{T}}({\theta }_0))\mathsf{subject}\mathsf{to}{\theta }^{\mathcal{S}}(\mathcal{S})=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{S}}(\theta ({\theta }_0))\text{\hspace{1em}(5)}$$其中，${\theta }^{\mathcal{T}}=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{T}}(\theta ({\theta }_0))$。

• 简而言之，在下一节中，本文仅使用${\theta }^{\mathcal{S}}$和${\theta }^{\mathcal{T}}$分别表示${\theta }^{\mathcal{S}}({\theta }_0)$和${\theta }^{\mathcal{T}}({\theta }_0)$。

• 求解式(5)的标准方法采用隐式微分（详见（Domke，2012）），其中涉及求解${\theta }^{\mathcal{S}}$的内环优化。

• 由于内环优化${\theta }^{\mathcal{S}}=\arg \underset{\theta }{\min }{\mathcal{L}}^{\mathcal{S}}(\theta )$在大规模模型的情况下可能计算昂贵，因此可以采用（Domke，2012）中的反向优化方法，将${\theta }^{\mathcal{S}}$重新定义为不完全优化的输出：
  $${\theta }^{\mathcal{S}}(\mathcal{S})={opt-alg}_{\theta }({\mathcal{L}}^{\mathcal{S}}(\theta ),\varsigma )\text{\hspace{1em}(6)}$$其中，$opt-alg$是具有固定steps数($\varsigma$)的特定优化过程。

• 在实践中，不同初始化的${\theta }^{\mathcal{T}}$可以首先在离线阶段训练，然后在式(5)中用作目标参数向量。

• 然而，通过学习回归${\theta }^{\mathcal{T}}$作为目标向量有两个潜在的问题。
  （1）${\theta }^{\mathcal{T}}$和${\theta }^{\mathcal{S}}$中间值之间的距离在参数空间中可能太大，路径上有多个局部最小陷阱，因此很难达到。
  （2）$opt-alg$涉及有限数量的优化步骤，作为速度和精度之间的权衡，这可能不足以采取足够的步骤来达到最优解。这些问题类似于（Wang et al.，2018）的问题，因为它们都涉及用$\mathcal{S}$和${\theta }_0$参数化${\theta }^{\mathcal{S}}$。

2.3 具有课程梯度匹配的Dataset condensation

• 本文提出了一种基于课程的方法来解决上述挑战。
• 关键思想是：希望${\theta }^{\mathcal{S}}$不仅接近最终的${\theta }^{\mathcal{T}}$，而且在整个优化过程中遵循与${\theta }^{\mathcal{T}}$相似的路径。
• 虽然这可能限制$\theta$的优化动态，但本文认为它也可以实现更有指导意义的优化和不完全优化器的有效使用。
• 现在可以将式(5)分解为多个子问题：
  $$\begin{gathered} \underset{\mathcal{S}}{\min }{E}_{{\theta }_0\sim P_{{\theta }_0}}[\sum _{t=0}^{T-1}D({\theta }_t^{\mathcal{S}},{\theta }_t^{\mathcal{T}})] \\ \mathsf{subject}\mathsf{to} \\ {\theta }_{t+1}^{\mathcal{S}}(\mathcal{S})-{opt-alg}_{\theta }({\mathcal{L}}^{\mathcal{S}}({\theta }_t^{\mathcal{S}}),{\varsigma }^{\mathcal{S}})\mathsf{and}{\theta }_{t+1}^{\mathcal{T}}-{opt-alg}_{\theta }({\mathcal{L}}^{\mathcal{T}}({\theta }_t^{\mathcal{T}}),{\varsigma }^{\mathcal{T}})\text{\hspace{1em}(7)} \end{gathered}$$其中，$T$为迭代次数；${\varsigma }^{\mathcal{S}}$和${\varsigma }^{\mathcal{T}}$分别为${\theta }^{\mathcal{S}}$和${\theta }^{\mathcal{T}}$的优化步数。
• 换句话说，本文希望生成一组压缩样本S，使得在其上训练的网络参数$({\theta }_t^{\mathcal{S}})$与每 $t$ 次迭代时在原始训练集上训练的网络参数$({\theta }_t^{\mathcal{T}})$相似。
• 在初步实验中，本文观察到用$\mathcal{S}$参数化的${\theta }_{t+1}^{\mathcal{S}}$可以通过更新$\mathcal{S}$并最小化$D({\theta }_t^{\mathcal{S}},{\theta }_t^{\mathcal{T}})$接近于零来成功跟踪${\theta }_{t+1}^{\mathcal{T}}$。
• 在$opt-alg$一步梯度下降优化的情况下，更新规则是
  $${\theta }_{t+1}^{\mathcal{S}}\leftarrow {\theta }_t^{\mathcal{S}}-{\eta }_{\theta }{▽}_{\theta }{\mathcal{L}}^{\mathcal{S}}({\theta }_t^{\mathcal{S}})and{\theta }_{t+1}^{\mathcal{T}}\leftarrow {\theta }_t^{\mathcal{T}}-{\eta }_{\theta }{▽}_{\theta }{\mathcal{L}}^{\mathcal{T}}({\theta }_t^{\mathcal{T}})\text{\hspace{1em}(8)}$$其中，${\eta }_{\theta }$为学习率。
• 基于本文的观察（$D({\theta }_t^{\mathcal{S}},{\theta }_t^{\mathcal{T}})\approx 0$），通过将${\theta }_t^{\mathcal{T}}$替换为${\theta }_t^{\mathcal{S}}$，并在本文剩余部分使用$\theta$表示${\theta }^{\mathcal{S}}$简化式(7)：
  $$\underset{\mathcal{S}}{\min }{E}_{{\theta }_0\sim P_{{\theta }_0}}[\sum _{t=0}^{T-1}D({▽}_{\theta }{\mathcal{L}}^{\mathcal{S}}({\theta }_t),{▽}_{\theta }{\mathcal{L}}^{\mathcal{T}}({\theta }_t))]\text{\hspace{1em}(9)}$$
• 我们现在有一个单一的深度网络，参数$\theta$在合成集$\mathcal{S}$上训练，该网络经过优化，使得关于$\theta$的训练样本${\mathcal{L}}^{\mathcal{T}}$上的损失梯度和关于$\theta$的合成样本${\mathcal{L}}^{\mathcal{S}}$上的损失梯度之间的距离最小化（梯度匹配）。
• 这种近似与（Wang et al.，2018）和式(5)相比具有关键优势，即它不需要对先前参数 { θ 0 , . . . , θ t − 1 } \{\theta_0,...,\theta_{t-1}\} {θ0​,...,θt−1​}进行昂贵的递归计算图展开。
• 本文方法优化速度明显更快，内存效率高，因此可以扩展到最先进的深度神经网络（例如ResNet（He et al.，2016））。
• 讨论
• 合成数据不仅包含样本，还包含其标签$(s,y)$，理论上可以通过优化式(9)来联合学习。
• 然而它们的联合优化具有挑战性，因为样本的内容取决于它们的标签，反之亦然。
• 因此，本文实验学习为固定标签合成图像，例如每个类一张合成图像。

• 梯度匹配损失
• 式(9)中的匹配损失$D(\cdot ,\cdot )$度量关于$\theta$的${\mathcal{L}}^{\mathcal{S}}$和${\mathcal{L}}^{\mathcal{T}}$的梯度之间的距离。
• 当${\varphi }_{\theta }$是一个多层神经网络时，梯度对应于每个全连接层（FC）和卷积层的一组可学习的2D(out×in)和4D(out×in×h×w)权重，其中out、in、h、w是输出和输入通道数、核高度和宽度。
• 匹配损失可以分解为分层损失之和，即$D({▽}_{\theta }{\mathcal{L}}^{\mathcal{S}},{▽}_{\theta }{\mathcal{L}}^{\mathcal{T}})={\sum }_{i=1}^{L}d({▽}_{{\theta }^{(l)}}{\mathcal{L}}^{\mathcal{S}},{▽}_{{\theta }^{(l)}}{\mathcal{L}}^{\mathcal{T}})$，其中 $l$ 是层索引，$L$ 是具有权重的层数，并且
  $$d(\mathbf{A},\mathbf{B})=\sum _{i=1}^{out}(1-\frac{{\mathbf{A}}_{i\cdot }\cdot {\mathbf{B}}_{i\cdot }}{\parallel {\mathbf{A}}_{i\cdot }\parallel \cdot \parallel {\mathbf{B}}_{i\cdot }\parallel })\text{\hspace{1em}(10)}$$ 其中，
  ${\mathbf{A}}_{i\cdot }$、${\mathbf{B}}_{i\cdot }$是对应于每个输出节点$i$梯度的平滑向量，对于FC权重是in维度，对于卷积权重是in×h×w维度。
• （Lopez-Paz et al.，2017； Aljandy et al.，2019；朱et al.，2019）通过将所有层上的张量平滑为一个向量，然后计算两个向量之间的距离来忽略分层结构，与该方法相比，本文为每个输出节点进行分组。
• 本文发现，这对于梯度匹配来说是一个更好的距离（参见补充），并且可以在所有层上使用单一的学习率。

实验