图像缩放之双三次插值法

最新推荐文章于 2024-02-23 10:50:46 发布

天经地义之经

最新推荐文章于 2024-02-23 10:50:46 发布

阅读量1.1k

点赞数

分类专栏： SIFT

SIFT 专栏收录该内容

9 篇文章 0 订阅

订阅专栏

http://blog.csdn.net/qq_29058565/article/details/52769497

今天学习了第三种图像缩放的方法，双三次插值法。由于理解能力比较差，看了好久的公式，还是云里雾里，但是为了督促自己学习，还是把已知的部分记录下来。

数学原理

维基百科的解释

假设源图像A大小为m*n，缩放后的目标图像B的大小为M*N。那么根据比例我们可以得到B(X,Y)在A上的的
对应坐标为A(x,y)=A(X*(m/M),Y*(n/N))。在双线性插值法中，我们选取A(x,y)的最近四个点。而在双立方
插值法中，我们选取的是最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数。如图所示：

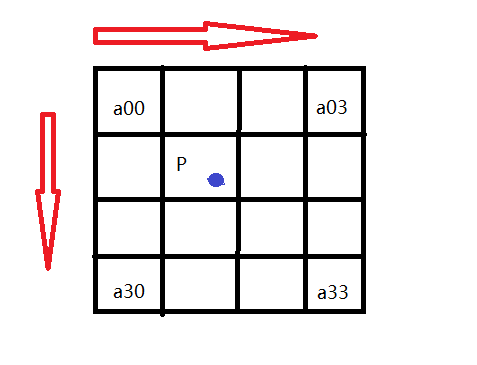
双立方插值说明图

如图所示P点就是目标图像B在(X,Y)处对应于源图像中的位置，P的坐标位置会出现小数部分，所以我们假设
P的坐标为P(x+u,y+v)，其中x,y分别表示整数部分，u,v分别表示小数部分。那么我们就可以得到如图所示的
最近16个像素的位置，在这里用a(i,j)(i,j=0,1,2,3)来表示。
双立方插值的目的就是通过找到一种关系，或者说系数，可以把这16个像素对于P处像素值得影响因子找出
来，从而根据这个影响因子来获得目标图像对应点的像素值，达到图像缩放的目的。
我在这次的学习中学习的是基于BiCubic基函数的双三次插值法，BiCubic基函数形式如下：

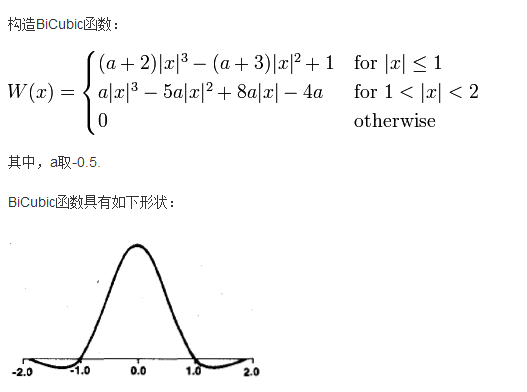
这里写图片描述

参考这里的博客

我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的系数。在学习双线性插
值法的时候，我们是把图像的行和列分开来理解的，那么在这里，我们也用这种方法描述如何求出a(i,j)对应
的系数k_ij。假设行系数为k_i,列系数为k_j。我们以a00位置为例：
首先，我们要求出当前像素与P点的位置，比如a00距离P(x+u,y+v)的距离为(1+u,1+v)。
那么我们可以得到：k_i_0=W(1+u),k_j_0=W(1+v).
同理我们可以得到所有行和列对应的系数：

k_i_0=W(1+u), k_i_1=W(u), k__i_2=W(1-u), k_i_3=W(2-u);
k_j_0=W(1+v), k_j_1=W(v), k_j_2=W(1-v), k_j_3=W(2-v);

这样我们就分别得到了行和列方向上的系数。
由k_i_j=k_i*k_j我们就可以得到每个像素a(i,j)对应的权值了。

最后通过求和公式可以得到目标图片B(X,Y)对应的像素值：
pixelB(X,Y)=pixelA(0,0)*k_0_0+pixelA(0,1)*k_0_1+…+pixelA(3,3)*k_3_3;
这里其实就是个求和公式，由于不知道怎么编辑公式，就这样表达了。

程序实现

/**********************10-9*******************************
功能：双三次插值缩放图片
数学原理：假设原图像A的大小为m*n,新图像B的大小为M*N
如果我们要求B（X,Y）处的像素值：
我们首先可以得到B（X,Y）在图像A中对应的位置（x,y）=(X*(m/M),Y*(N/n))
这个时候求得的x,y是小数值，我们可以通过这个小数值坐标找到距离最近的16个像素点，
利用所选择的基函数，求出对应的每个像素的权值，最终获得pixelB（X,Y）
**********************************************************/

#include <opencv2\opencv.hpp>
#include <iostream>
#include <math.h>
using namespace std;
using namespace cv;

float a = -0.5;//BiCubic基函数
void getW_x(float w_x[4], float x);
void getW_y(float w_y[4], float y);

int main(){
    Mat image = imread("lena.jpg");//源图像

    float Row_B = image.rows*2;
    float Col_B = image.cols*2;


    Mat biggerImage(Row_B, Col_B, CV_8UC3);

    for (int i = 2; i < Row_B-4; i++){
        for (int j = 2; j < Col_B-4; j++){
            float x = i*(image.rows / Row_B);//放大后的图像的像素位置相对于源图像的位置
            float y = j*(image.cols / Col_B);

            /*if (int(x) > 0 && int(x) < image.rows - 2 && int(y)>0 && int(y) < image.cols - 2){*/
                float w_x[4], w_y[4];//行列方向的加权系数
                getW_x(w_x, x);
                getW_y(w_y, y);

                Vec3f temp = { 0, 0, 0 };
                for (int s = 0; s <= 3; s++){
                    for (int t = 0; t <= 3; t++){
                        temp = temp + (Vec3f)(image.at<Vec3b>(int(x) + s - 1, int(y) + t - 1))*w_x[s] * w_y[t];
                    }
                }

                biggerImage.at<Vec3b>(i, j) = (Vec3b)temp;
            }
        }

    imshow("image", image);
    imshow("biggerImage", biggerImage);
    waitKey(0);

    return 0;
}
/*计算系数*/
void getW_x(float w_x[4],float x){
    int X = (int)x;//取整数部分
    float stemp_x[4];
    stemp_x[0] = 1 + (x - X);
    stemp_x[1] = x - X;
    stemp_x[2] = 1 - (x - X);
    stemp_x[3] = 2 - (x - X);

    w_x[0] = a*abs(stemp_x[0] * stemp_x[0] * stemp_x[0]) - 5 * a*stemp_x[0] * stemp_x[0] + 8 * a*abs(stemp_x[0]) - 4 * a;
    w_x[1] = (a + 2)*abs(stemp_x[1] * stemp_x[1] * stemp_x[1]) - (a + 3)*stemp_x[1] * stemp_x[1] + 1;
    w_x[2] = (a + 2)*abs(stemp_x[2] * stemp_x[2] * stemp_x[2]) - (a + 3)*stemp_x[2] * stemp_x[2] + 1;
    w_x[3] = a*abs(stemp_x[3] * stemp_x[3] * stemp_x[3]) - 5 * a*stemp_x[3] * stemp_x[3] + 8 * a*abs(stemp_x[3]) - 4 * a;
}
void getW_y(float w_y[4], float y){
    int Y = (int)y;
    float stemp_y[4];
    stemp_y[0] = 1.0 + (y - Y);
    stemp_y[1] = y - Y;
    stemp_y[2] = 1 - (y - Y);
    stemp_y[3] = 2 - (y - Y);

    w_y[0] = a*abs(stemp_y[0] * stemp_y[0] * stemp_y[0]) - 5 * a*stemp_y[0] * stemp_y[0] + 8 * a*abs(stemp_y[0]) - 4 * a;
    w_y[1] = (a + 2)*abs(stemp_y[1] * stemp_y[1] * stemp_y[1]) - (a + 3)*stemp_y[1] * stemp_y[1] + 1;
    w_y[2] = (a + 2)*abs(stemp_y[2] * stemp_y[2] * stemp_y[2]) - (a + 3)*stemp_y[2] * stemp_y[2] + 1;
    w_y[3] = a*abs(stemp_y[3] * stemp_y[3] * stemp_y[3]) - 5 * a*stemp_y[3] * stemp_y[3] + 8 * a*abs(stemp_y[3]) - 4 * a;
}
  
  1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
  
  1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82