PAC计算学习理论介绍

课程简介

• 课程链接：https://www.bilibili.com/video/BV1Ft41197Dy/?vd_source=0ff4043ca590a6bdd89be9465c9fc3e5

• 作者介绍：https://zh.wikipedia.org/zh-hans/%E6%9E%97%E8%BB%92%E7%94%B0

机器学习

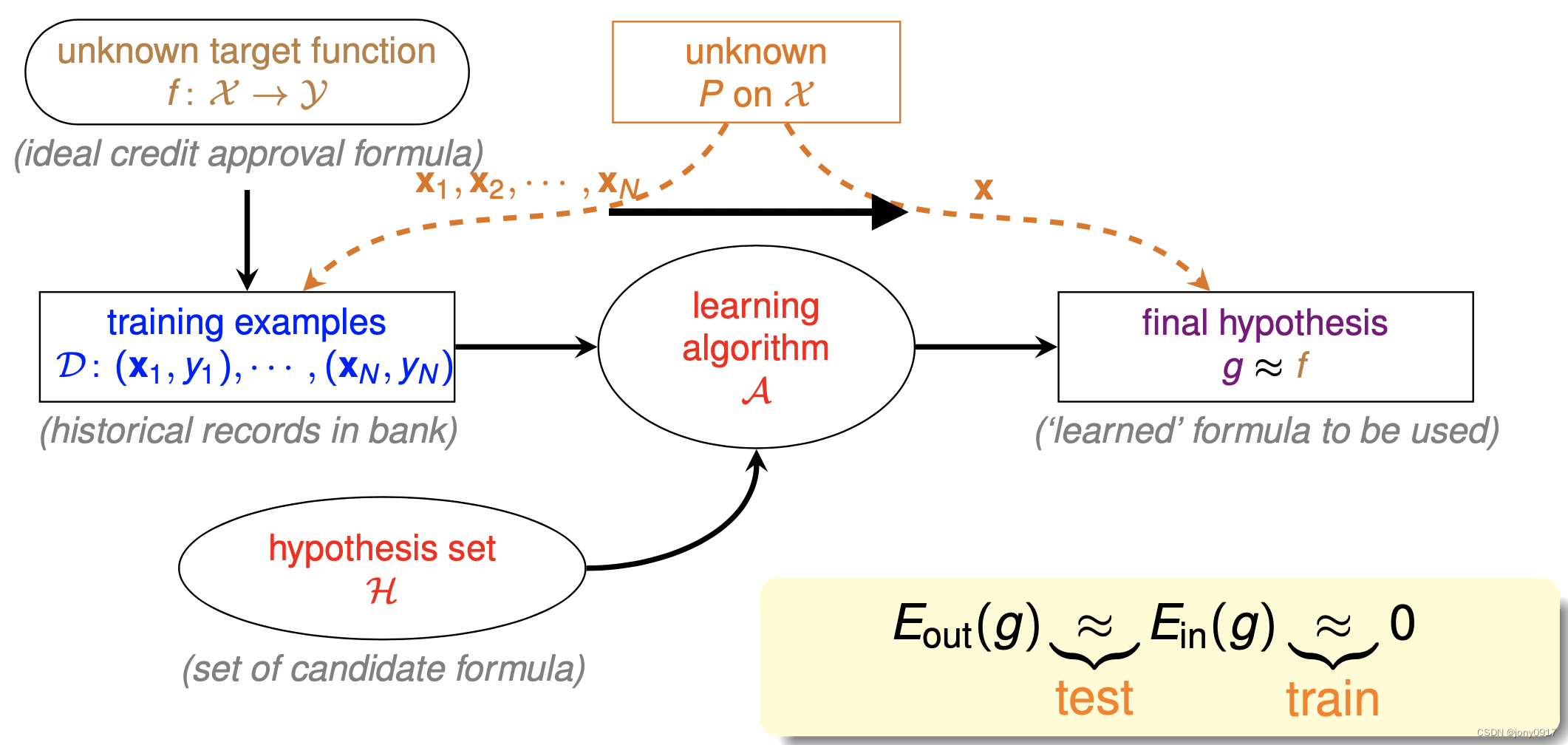
机器学习要素

• 目标函数 $f:\mathcal{X}\to \mathcal{Y}$

• 总体分布 $P$

• 训练样本 $\mathcal{D}=\{(x_i,y_i),i\in [N]\}$：从总体样本中抽样得到，N 表示样本规模

• 假设（函数）集合 H = { h k } \mathcal{H} = \{h_k\} H={hk​}

• 学习算法 $\mathcal{A}$

• 学习算法从假设集合中选择的假设（函数） g

• 误差

• • 经验误差：g 在训练样本 D 上的误差称为经验误差

  • • $E_{in}(g)=\frac{1}{N}{\sum }_{i}I(g(x_i)\ne y_i)$

  • 泛化误差： g 在训练样本外的所有其他样本上的误差称为泛化误差

  • • $E_{out}(g)=E_{x\sim P}[I(g(x_i)\ne y_i)]$

通常我们把假设集合 H = { h k } \mathcal{H} = \{h_k\} H={hk​} 和学习算法 $\mathcal{A}$一起称为模型,有时候模型也指假设集合本身。

举例

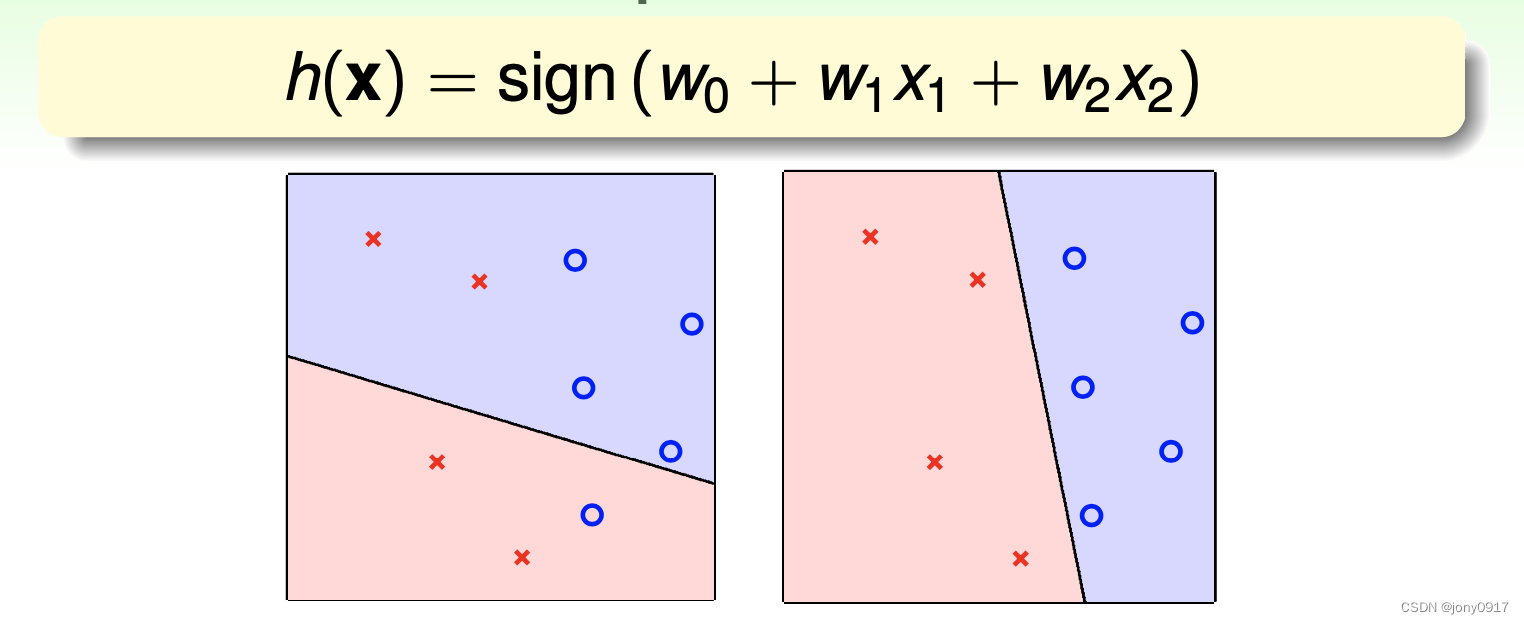
平面上存在两中类型的点，分别用圈和叉表示，采用感知器（Perceptron）模型进行分类：

• 训练数据 $\mathcal{D}=\{(x_{i,1},x_{i,2},y_i),i\in [N]\}$

• 假设集合 $\mathcal{H} = {h(x_1,x_2) = sign(w_0 + w_1x_1 + w_2x_2) = sign(w^Tx)} $，集合包含了二维平面上的所有的直线

• 学习算法 : PA 算法

算法略过不介绍，因为并非 PAC 理论的关键，事实上 PAC 计算学习理论主要关注点在于假设集合 的性质，更确切的说是假设集合不依赖具体的学习算法的性质，这个在后面的内容中将看到。另外这个二维平面感知器模型的例子，后续还会用到。

机器学习过程

• 机器学习的过程是学习算法 $\mathcal{A}$ 依据 $E_{in}(g)\approx 0$ 为标准，从假设集合 $\mathcal{H}$ 中选择假设 g ，并期望满足 $E_{out}(g)\approx 0$，以达到获取目标函数 f 的近似函数的目标.

可以看到假设（函数） g 需要满足两个条件，才是目标函数 f 的比较好的近似：

• 经验误差 $E_{in}(g)\approx 0$

• 泛化误差 $E_{out}(g)\approx 0$

经验误差由学习算法 A 保障，但泛化误差依赖训练样本之外所有样本，是无法直接计算的，也就无法直接优化，那么如何降低泛化误差呢 ？

霍夫丁不等式

一个罐子装有橙色和绿色两种颜色的球，但每种颜色的比例未知，比例将黄球的比例记为 ，因为球的数量巨大，如何估计黄球的比例 呢？

从罐子里随机取出 N 个球，这批 N 个球中黄球的比例记为，满足下面霍夫丁不等式：

$$P(|\nu -\mu |\ge ϵ)\le 2e^{-2{ϵ}^{2}N}(1)$$

其中为任意正数。从霍夫丁不等式（1）可以得出：

• 当样本规模 N 足够大的时候，与的偏差大于的概率接近零，也就是

回到泛化误差的问题，对于假设集合中的任意一个假设，同样满足:

$$P(|E_{in}(g)-E_{out}(g)|\ge ϵ)\le 2e^{-2{ϵ}^{2}N}(2)$$

不等式（2）可以得出：

• 训练样本规模 N 足够大的时候，满足

下面视角从单个假设 g 的维度，切换到假设集合 H = { h k } \mathcal{H} = \{h_k\} H={hk​}整体，PAC 理论关注假设集合作为一个整体有哪些性质。

假设集合 size 记为，考虑假设集合中至少存在一个假设的的概率，推导过程如下 ：

$$\begin{gathered} P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ) \\ =P(|E_{in}(h_1)-E_{out}(h_1)|\ge ϵ\cup |E_{in}(h_2)-E_{out}(h_2)|\ge ϵ\cup ...\cup |E_{in}(h_M)-E_{out}(h_M)|\ge ϵ) \\ \le \sum _i^{M}P(|E_{in}(h_i)-E_{out}(h_i)|\ge ϵ) \\ \le 2M{e}^{-2{ϵ}^{2}N} \end{gathered}$$

$$P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ)\le 2M{e}^{-2{ϵ}^{2}N}(3)$$

为什么要关注 “假设集合中至少存在一个假设$|E_{in}(h)-E_{out}(h)|>ϵ$” 事件的发生概率呢 ？

• PAC 关注的是能否从学习到好的假设 g，并以此来衡量是否是一个好的假设集合
• 因为如果此事件的概率很小，趋向于零，则无论我们的学习算法如何选择假设 g，均能能满足$E_{out}(g)\approx E_{in}(g)$ ，此条件是学习到好的假设 g 的必要条件之一
• 此事件发生的概率趋向于零，学习才有可能可行

不等式（3）可以得出：

• 当 M 有限时， N 足够大，则泛化误差与经验误差的差值趋近于零，这时学习算法 A 依据经验误差最小化的目标，选择假设 g 就是目标函数 f 的较好的近似

• M 较小时，少量的样本即可保证$E_{out}(g)\approx E_{in}(g)$ ，但不一定存在 g 满足 ，因为可选择假设较少

• M 较大时，可选择额假设较多，存在 g 满足$E_{in}(g)\approx 0$概率增大，但需要更多的样本才能保证 $E_{out}(g)\approx E_{in}(g)$

• M 值的选择非常重要，不大不小，刚好合适，才能满足$E_{in}(g)\approx 0$和$E_{out}(g)\approx E_{in}(g)$两个条件

实际中常见的假设集合为无限大，有限的假设集合反而很少见，M 为无限大时：

• 不等式（3）概率上界$2M{e}^{-2{ϵ}^{2}N}$为无穷大，不够tight，失去意义
• 需要寻找一个更 tight 的概率上界

回顾不等式（3）的推导过程：

$$\begin{gathered} P(|E_{in}(h_1)-E_{out}(h_1)|\ge ϵ\cup |E_{in}(h_2)-E_{out}(h_2)|\ge ϵ\cup ...|E_{in}(h_M)-E_{out}(h_M)|\ge ϵ) \\ \le \sum _{i=1}^{M}P(|E_{in}(h_i)-E_{out}(h_i)|\ge ϵ) \end{gathered}$$

此不等式在 M 个概率事件 $|E_{in}(h_i)-E_{out}(h_i)|\ge ϵ,i\in [1,M]$ 互斥的的情况下取等号，其他情况下取小于号，但很多情况是不能满足互斥条件的，导致此概率上界依然不够 tight 。实际情况是很多时候事件之间存在重叠情况，因为$P(A\cup B)=P(A)+P(B)-P(A\cap B)$，得出实际的上界往往要远小于 ${\sum }_{i=1}^{M}P(|E_{in}(h_i)-E_{out}(h_i)|\ge ϵ)$。

下面考虑概率事件 $|E_{in}(h_i)-E_{out}(h_i)|\ge ϵ,i\in [M]$ 之间的重叠情况，我们依据假设$h_i,i\in [M]$对样本的判断结果情况，对假设 $h_i,i\in [M]$ 进行分类，以二维平面点分类为例说明：

样本数量 N	图示	假设分类数量
1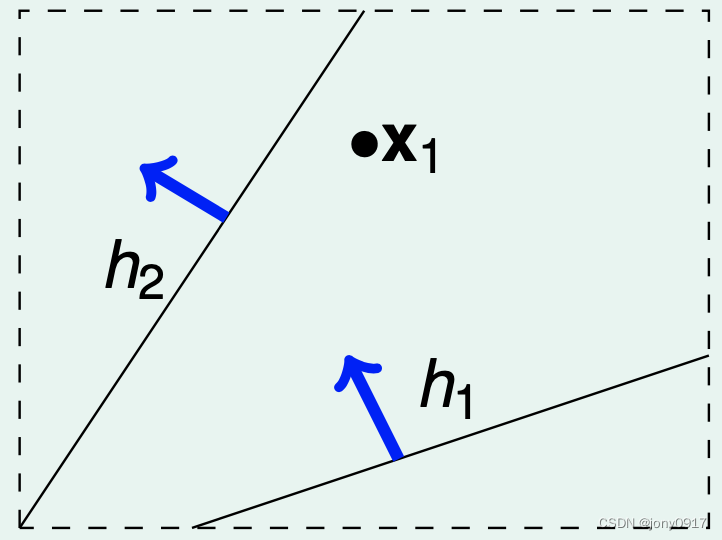
2一类假设将 判断为 0另一类假设将 判断为 1
2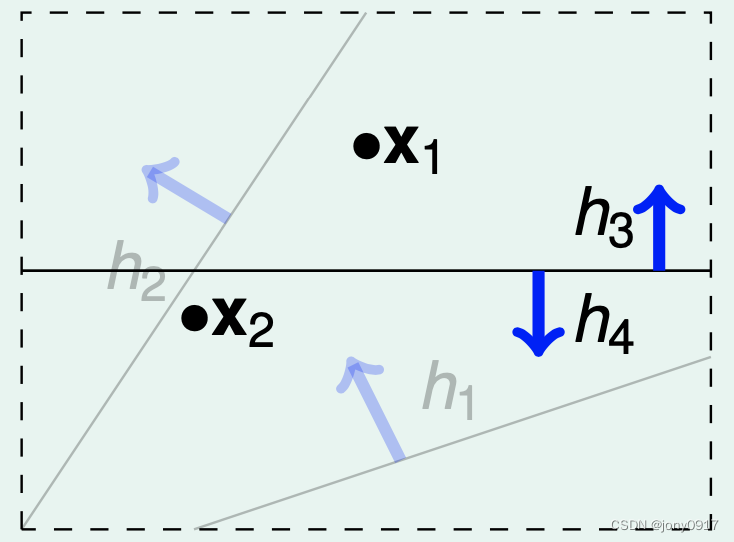
4（0，0）（0，1）（1，0）（1，1）
3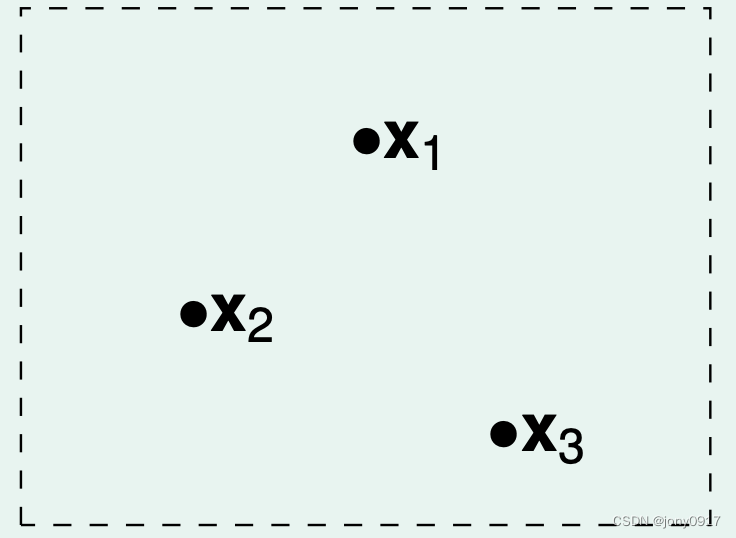
8（0，0，0）（0，0，1）…
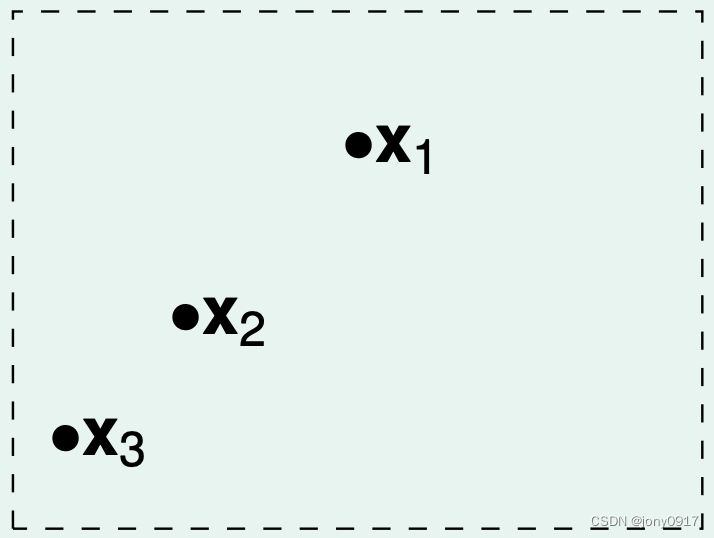6
4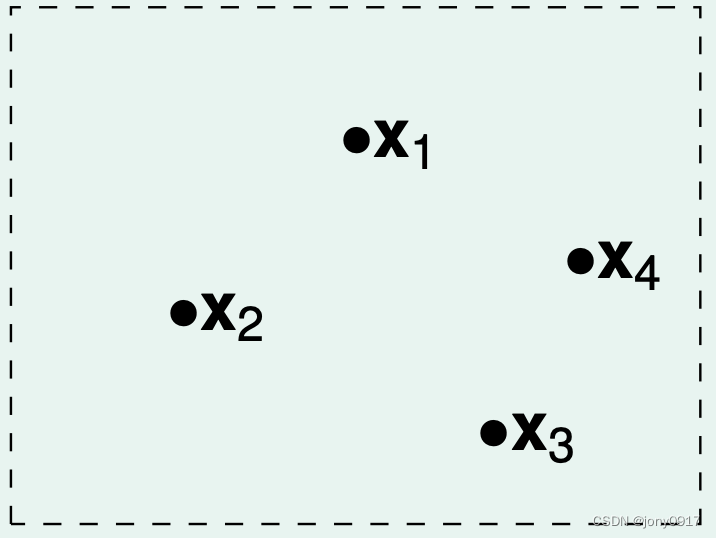
<=14

可以看出此例子中：

• 假设集合包含二维平面上的所有直线，因此 M 为无限大
• 样本数量 N 确定之后，依据假设对 N 个样本的分类结果，可以对假设进行分类，类型数量并不是无限大，类型数量上限是 $2^N$

将假设类型数量记为:

• 同类假设对 N 个样本分类结果相同，因此满足$E_{in}(h_i)=E_{in}(h_j)$

• 一个自然的疑问是：用代替 M，不等式（3）是否依然成立？

$$P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ)\stackrel{\text{?}}{\le }2\cdot effective(N)\cdot e^{-2{ϵ}^{2}N}(4)$$

回答这个问题之前需要再引入几个概念

Dichotomies

定义： h ∈ H = { h : X → { 0 , 1 } } h\in\mathcal{H} = \{h:\mathcal{X}\rightarrow \{0, 1\}\} h∈H={h:X→{0,1}}，称 h ( x 1 , . . . , x n ) = ( h ( x 1 ) , . . . , h ( x n ) ) ∈ { 0 , 1 } N h(x_1,...,x_n) = (h(x_1),...,h(x_n)) \in \{0,1\}^N h(x1​,...,xn​)=(h(x1​),...,h(xn​))∈{0,1}N 为一个 dichotomy，假设集合对样本 D 上所有的 dichoromy 构成的集合记为 $\mathcal{H}(x_1,...,x_N)$.

举例：二维平面上点的二分类任务，采用感知器模型，样本规模 N = 4

	H = { y = s i g n ( w T x ) } \mathcal{H} = \{y = sign(w^Tx)\} H={y=sign(wTx)}	$\mathcal{H}(x_1,x_2,x_3,x_4)$
集合组成元素	二维平面上的所有直线	(0,0,0,0), (,0,0,0,1), …, (1,1,1,1,)
集合 size	无限大	<=14

$|\mathcal{H}(x_1,..,x_N)|$ 与假设集合有关，与具体的样本 $（x_1,..,x_N）$ 也有关：

N	$\mathcal{H}(x_1,..,x_N)$
1	2
2	4
3	<=8
4	<=14

增长函数

定义：$m_{\mathcal{H}}(N)=ma{x}_{x_1,..,x_N\in \mathcal{X}}|\mathcal{H}(x_1,...,x_N)|$ 称为假设集合的增长函数。

由定义可以看出：

• $m_{\mathcal{H}}(N)\le 2^N$

• 增长函数依赖假设集合、样本规模N，去掉了对具体样本的依赖

• 直观上，增长函数衡量了假设集合的表达能力，增长函数越大，假设集合的表达能力越强，的概率越大

Shatter

定义：$|\mathcal{D}|=N$，如果 $m_{\mathcal{H}}(N)=2^N$，则称假设集合 shatter 样本集合 D.

• Shatter 概念的直观理解是$\mathcal{H}(x_1,...,x_N)$ 集合包含了样本集 D 的所有可能的分类结果，因此必然包括正确的分类结果，从而保证了一定能找到 $E_{in}(g)\approx 0$ 的假设 g .
• 假设集合能够 shatter 的样本规模 N 越大，表明假设集合的表达能力越强

Breaking Point

定义：假设空间 $\mathcal{H}$ 的增长函数记为 $m_{\mathcal{H}}(N)$，满足条件 $m_{\mathcal{H}}(k)<2^k$ 的 k 称为假设集合的一个 breaking point .

• breaking point 表示假设结合无法 shatter 的样本 size.
• 如果 k 为breaking point，则 k + 1, k + 2, k + 2,… 均为 breaking point.
• 因此 minimum breaking point 具有特殊意义，后续 breaking point 无特殊说明均指 minimum breaking point.
• minimum breakong point k 值越大，表明假设集合能够 shatter 的样本规模越大，假设集合的表达能力越强

Bounding 函数

定义：$B(N,k)=ma{x}_{(\mathcal{H}s.t.BreakingPoint(H)=k)}{m}_{\mathcal{H}}(N)$，给定 breaking point = k 条件下的最大值称为 bounding 函数。

• Bounding 函数依赖样本规模 N 和 breaking point k，不依赖具体的假设集合，关注点是给定 breaking point 条件下增长函数的最大值

Bounding 函数满足以下不等式关系：

$$m_{\mathcal{H}}(N)\le B(N,k)\le \sum _{i=0}^{k-1}\left(\genfrac{}{}{0ex}{}{N}{i}\right)\le N^{k-1}(5)$$

到此为止终于可以回到上面提出的问题：不等式（4）是否成立？

答案是不能直接替换，但有以下不等式成立：

$$P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ)\le 2\cdot 2m_{\mathcal{H}}(2N)\cdot e^{-2\frac{1}{16}{ϵ}^{2}N}=\frac{2\cdot 2m_{\mathcal{H}}(2N)\cdot }{e^{2\frac{1}{16}{ϵ}^{2}N}}(6)$$

综合不等式（5）和（6）得出：

$$P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ)\le \frac{4(2N{)}^{k-1}\cdot }{e^{2\frac{1}{16}{ϵ}^{2}N}}(7)$$

不等式 7 可以得出：

• 假设空间的 breaking point k 存在且为有限值时，随着样本规模 N 的增大，不等式（7）中右侧概率上界的分子的增长速度远小于分母的增长速度，事件发生的概率趋向于零，泛化误差近似等于经验误差，学习是可行的

目前为止总结一下学习可行需要满足的条件是：

• breaking point k 足够大，保障学习算法能够从假设空间中选出 g 满足 $E_{in}(g)\approx 0$

• breaking point k 有限大，样本规模 N 足够大，保障泛化误差接近经验误差

VC 维度

定义：满足条件 $m_{\mathcal{H}}(N)=2^N$ 最大的 N，称为假设空间的VC维度，记为 $d_{VC}(\mathcal{H})$.

根据定义可得出以下性质：

• 假设集合 $\mathcal{H}$ 可 shatter 的最大样本容量
• $d_{VC}(\mathcal{H})$ = breaking point k - 1.
• 衡量模型的表达能力，越大，模型的表达能力越强

不等式（7）中带入VC维定义，得到不等式：

$$P(\exists h\in \mathcal{H}s.t.|E_{in}(h)-E_{out}(h)|\ge ϵ)\le \frac{2\cdot 2(2N{)}^{d_{VC}(\mathcal{H})}\cdot }{e^{2\frac{1}{16}{ϵ}^{2}N}}(8)$$

不等式（8）得出可以得出：

• 假设集合的的VC维有限，则随着样本规模 N 的增长，泛化误差趋向于经验误差，学习可行

再一次总结学习可行需要满足的条件：

• $d_{VC}(\mathcal{H})$ 足够，保障学习算法 能够从假设空间 中选出 g 满足 $E_{in}(g)\approx 0$

• $d_{VC}(\mathcal{H})$ 有限，样本规模 N 足够大，保障泛化误差接近经验误差

VC维的估计

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UlTKIYTX-1680080567830)(9.png)]

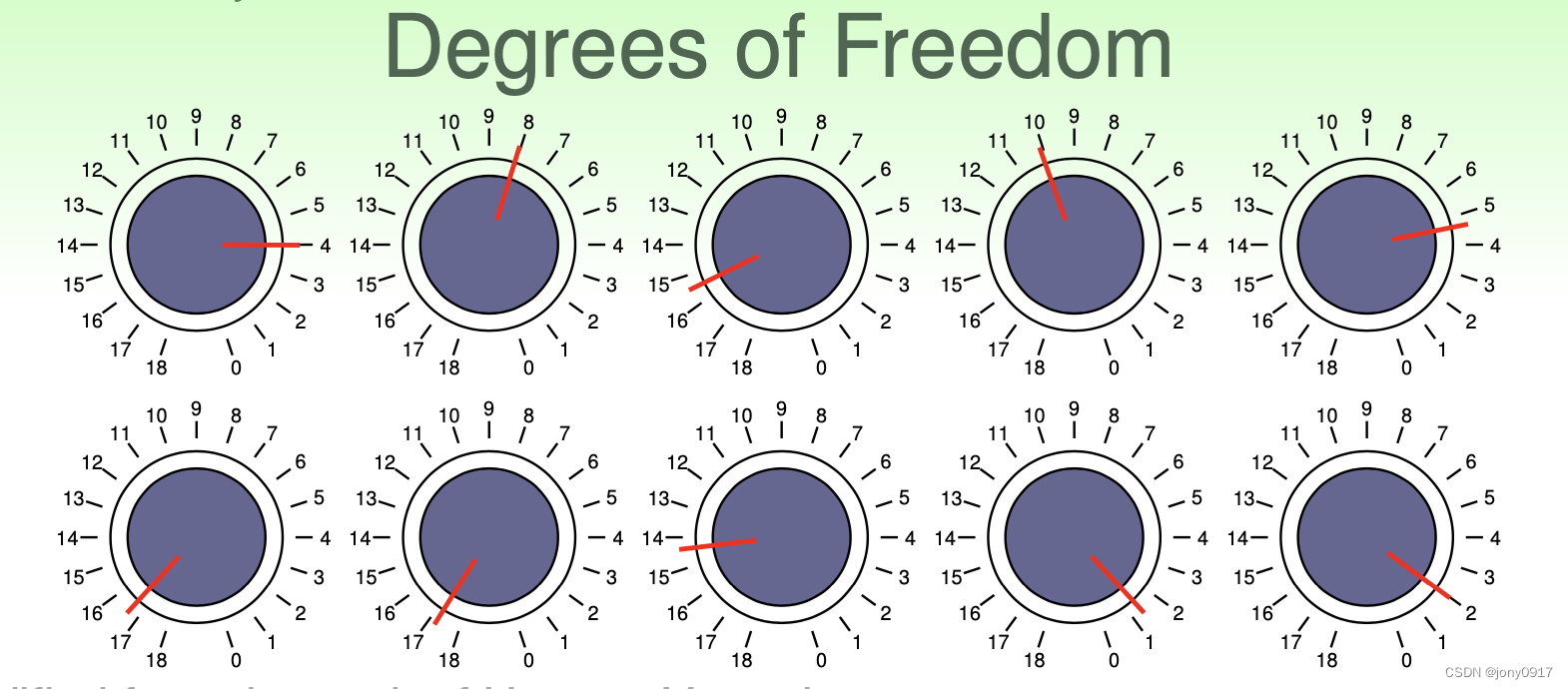
• 假设的参数 决定假设的自由度
• practical rule of thumb ： $d_{VC}(\mathcal{H})\approx d$

过拟合于欠拟合

从不等式（7）继续推导：

$$\begin{gathered} \frac{2\cdot 2(2N{)}^{d_{VC}(\mathcal{H})}\cdot }{e^{2\frac{1}{16}{ϵ}^{2}N}}=\delta \\ ϵ=\sqrt{\frac{8}{N}ln(\frac{4(2N{)}^{d_{VC}(\mathcal{H})}}{\delta })} \end{gathered}$$

$$E_{in}(g)-\sqrt{\frac{8}{N}ln(\frac{4(2N{)}^{d_{VC}(\mathcal{H})}}{\delta })}\le E_{out}(g)\le E_{in}(g)+\sqrt{\frac{8}{N}ln(\frac{4(2N{)}^{d_{VC}(\mathcal{H})}}{\delta })}$$

$$E_{in}(g)-\Omega (N,\mathcal{H},\delta )\le E_{out}(g)\le E_{in}(g)+\Omega (N,\mathcal{H},\delta )(9)$$

$$\Omega (N,\mathcal{H},\delta )\triangleq \sqrt{\frac{8}{N}ln(\frac{4(2N{)}^{d_{VC}(\mathcal{H})}}{\delta })}（10）$$

$\Omega (N,\mathcal{H},\delta )$ 函数衡量了假设空间的复杂度，随着 VC 纬度增大而增大。假设空间越复杂，泛化误差与经验误差的差距越大。下图所示，给定样本规模 N 与概率 $\delta$，随着假设空间的 VC 维度的不断上升，假设空间的复杂度 增大，经验误差不断减小，泛化误差先降低然后增大。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xf5ol62n-1680080567830)(10.png)]

过拟合: $d_{VC}>d_{VC}^{\ast }$，经验误差低，泛化误差高

欠拟合: $d_{VC}<d_{VC}^{\ast }$，经验误差高，泛化误差高