1.梯度下降:
等同于批梯度下降。
对于目标函数:
如果对于这个目标函数:求,
,
,
随机梯度下降:
由于J 是N 个函数的组合,所以我们可以把他们分成M 个部分(最多N 个部分),假如是N个部分,也就是一个元素一部分。
对于一组固定的,我们就得到
然后可以求出一组,
,
,
,对于第二个元素,我们用新得到的
,来作为初始值,再求梯度下降
对于第三个元素,利用第二个得到的,作为初始值,进行计算。
2.随机梯度下降的问题:SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
每次不一定都是下降方向?
参考博文:http://blog.csdn.net/lilyth_lilyth/article/details/8973972
梯度下降 求下降方向的时候需要求导。
在求步长的时候,需要求hessian 阵,需要求二阶导数?
t=(-d)'*d/((-d)'*Q*d);%求搜索步长
fx1=diff(f,'x1'); %对x1求偏导数
fx2=diff(f,'x2'); %对x2求偏导数
对于每一个函数,比如J,








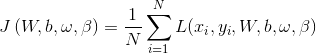














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








