组合数学_第4章_Polya定理

gengduc

已于 2023-04-18 18:36:41 修改

阅读量770

点赞数 3

分类专栏：组合数学文章标签：学习

于 2023-04-18 18:35:09 首次发布

本文链接：https://blog.csdn.net/gengduc/article/details/130228154

版权

组合数学专栏收录该内容

5 篇文章

订阅专栏

文章目录

第4章 Polya定理

第4章 Polya定理

4.1 群的概念

4.1.1 群的定义

给定一个集合 $G=\{a,b,c,\cdots\}$ 和集合 $G$ 上的二元运算“ $\cdot$ ”，并满足下列4个条件：

封闭性：若 $\in G$ ，则存在 $\in G$ ，使得，
$\cdot b=c$
结合律：对于任意的 $\in G$ ，恒有
$\cdot b) \cdot c = a \cdot (b \cdot c)$
存在单位元素： $G$ 中存在一个元素 $e$ ，使得对于 $G$ 的任意元素 $a$ ，恒有
$\cdot e = e \cdot a = a$
存在逆元素：对于 $G$ 的任意元素 $a$ ，恒有一个 $\in G$ ，使得
$\cdot b = b \cdot a = e$
元素 $b$ 称为元素 $a$ 的逆元素，记作 $a^{-1}$ ，即
$b= a^{-1}$

则称集合 $G$ 在运算 $\cdot$ 之下是一个群，有时也称 $G$ 是一个群， $G$ 中元素 $a$ 对 $b$ 的运算 $\cdot b$ ，可以简记为 $ab$ 。

例题： $G=\{1,-1\}$ 在乘法运算下是一个群。

解：（1）封闭性：(1)(-1)=-1,(1)(1)=1,(-1)(1)=-1,(-1)(-1)=1

（2）结合性：显然

（3）单位元素： $e = 1$

（4）逆元素：由于(1)(1)=1,(-1)(-1)=1，故 $1)^{-1}=-1,(1)^{-1}=1$

群的元素个数是有限的，称为有限群。有限群 $G$ 的元素个数叫做群的阶，记为 $∣ G ∣$ 。当群的元素为无限时，称为无限群。

若群 $G$ 的任意二元素 $a, b$ 恒满足 $ab = ba$ 时，称 $G$ 为交换群或Abel群。

4.1.2 群的性质

群的单位元是唯一的。
$\Rightarrow b=c,ba=ca \Rightarrow b=c$
$G$ 中每一个元素的逆元素是唯一的。
$abc \cdots lmn)^{-1}=n^{-1}m^{-1}l^{-1} \cdots c^{-1}b^{-1}a^{-1}$
…

设 $G$ 是群， $H$ 是 $G$ 的子集，若 $H$ 在 $G$ 的原来定义的运算下也成群，则称 $H$ 是 $G$ 的子群。

4.2 置换群

置换群是十分重要的群，特别是所有的有限群都可以用它来表示。

不失一般性，假定 $n$ 个元素为 $1, 2, ..., n$ 。若元素 $1$ 被 $1$ 到 $n$ 中某一整数 $a_1$ 所取代， $2$ 被其中的 $a_2$ 元素所取代，…， $n$ 被 $a_n$ 所取代，且
$a_i \neq a_j，若i \neq j，i,j \neq 1,2,\cdots,n$
用
$=\begin{pmatrix} 1 & 2 & 3 & \cdots & n \\ a_1 & a_2 & a_3 & \cdots & a_n \end{pmatrix}\\$
来表示。

置换群的定义为：设
$p_1 =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}, p_2 =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix}$

$p_1p_2 =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix} \\ =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 3 & 1 & 2 & 4 \end{pmatrix}\begin{pmatrix} 3 & 1 & 2 & 4 \\ 2 & 4 & 3 & 1 \end{pmatrix} \\ =\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 3 & 1 \end{pmatrix}$

先做 $p_1$ 的置换，再作 $p_2$ 的置换：
$\stackrel{p_1} {\longrightarrow} 3 \stackrel{p_2} {\longrightarrow} 2 \\ 2 \stackrel{p_1} {\longrightarrow} 1 \stackrel{p_2} {\longrightarrow} 4 \\ 3 \stackrel{p_1} {\longrightarrow} 2 \stackrel{p_2} {\longrightarrow} 3 \\ 4 \stackrel{p_1} {\longrightarrow} 4 \stackrel{p_2} {\longrightarrow} 1 \\$
简单来说就是先经过了 $p_1$ 的映射再经过了 $p_2$ 的映射。

循环节数：
$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 5 & 1 & 4 & 2 \end{pmatrix}=(13)(25)(4)$
1置换为3，同时3又能置换为1，这就是一个循环。4置换为4本身，这也算一个循环。左右两个表示是等价的，从后面的表示可以清楚的看到每个循环，以及循环节的个数。

4.3 Polya定理

设 $\overline{G}$ 是 $n$ 个对象的一个置换群，用 $m$ 种颜色涂染这 $n$ 个对象，则不同染色的方案数为
$l=\frac{1}{|\overline{G}|}[m^{c(\overline{a_1})}+m^{c(\overline{a_2})}+\cdots+m^{c(\overline{a_g})}]$
其中， $\overline{G}=\{\overline{a_1},\overline{a_2},\cdots,\overline{a_g}\}$ ， $c(\overline{a_k})$ 为置换 $\overline{a_k}$ 的循环节数。

$n$ 个对象可用 $1, 2, ..., n$ 编号，故 $\overline{G}$ 可当作 $(1,2,\cdots,n)$ 的一个置换群。

例题：用2种颜色去染排成一个环的6个棋子，如果通过旋转得到则只算一种，一共有多少种染色方案？

解：典型的满足polya公式的条件， $m = 2$ ， $n = 6$ 。因为是旋转得到的置换，所以存在6个置换（自己置换到自己也算）。
$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 2 & 3 & 4 & 5 & 6 & 1 \end{pmatrix}=(123456)$

$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 3 & 4 & 5 & 6 & 1 & 2 \end{pmatrix}=(135)(246)$

$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 4 & 5 & 6 & 1 & 2 & 3\end{pmatrix}=(14)(25)(36)$

$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 5 & 6 & 1 & 2 & 3 & 4 \end{pmatrix}=(153)(246)$

$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 6 & 1 & 2 & 3 & 4 & 5\end{pmatrix}=(165432)$

$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 1 & 2 & 3 & 4 & 5 & 6\end{pmatrix}=(1)(2)(3)(4)(5)(6)$

每个置换的循环节已经标出了。所以根据polya定理公式可以算出，染色方案数为 $\frac{1}{6}(2^1+2^2+2^3+2^2+2^1+2^6)=14$ 。

例题：一个3×3的方格，用10种颜色给每个格子染色，旋转0度、90度、180度、270度后相同的算成相同，问总共有多少种方案？

解：

旋转0度：(1)(2)(3)(4)(5)(6)(7)(8)(9)
旋转90度：(3179)(6248)(5)
旋转180度：(19)(28)(37)(46)(5)
旋转270度：(7931)(4862)(5)

所以根据Polya定理，总方案数就是 $\frac{1}{4}(10^9+10^3+10^5+10^3)$ 。

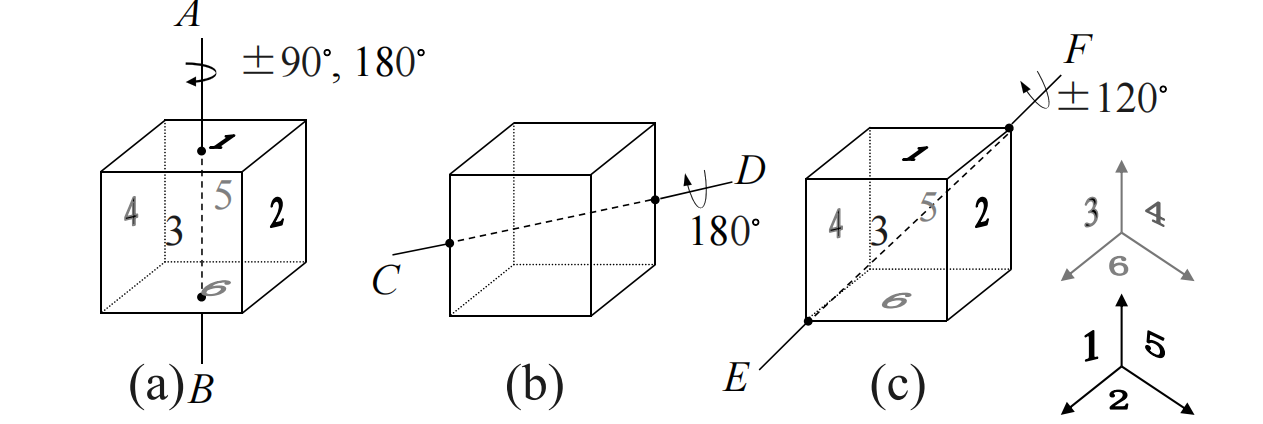
例题：正六面体的6个面分别用红蓝两种颜色着色，问有多少种方案？

解：使正六面体重合的刚体运动群，有如下几种情况：

不动置换(1)(2)(3)(4)(5)(6)，格式为 $1)^6$ ，只有1种。
绕过面1-面6中心的AB轴旋转90度，对应有(1)(2345)(6)，旋转-90度，对应有(1)(5432)(6)，格式为 $1)^2(4)^1$ ，正六面体有3个对面，故同类的置换有6个。
绕AB轴旋转180度，对应有(1)(24)(35)(6)，格式为 $1)^2(2)^2$ ，同类置换有3个。
绕CD轴（棱中-棱中）旋转180度的置换为(16)(25)(34)，格式为 $2)^3$ ，正六面体中对角线位置的平行的棱有6对，故同类的置换有6个。
绕正六面体的对角线EF（顶点-顶点）旋转120度，对应有(346)(152)，旋转-120度，对应有(643)(251)，格式为 $3)^2$ ，正六面体的对角线有4条，故同类的置换有8个。

根据polya定理，不同的颜色方案为
$M=\frac{1}{24}(2^6+6\cdot2^3+3\cdot2^4+6\cdot2^3+8\cdot2^2) \\ =\frac{1}{24}(64+48+48+48+32) = 10$
一种简单的推广：用 $m$ 种颜色对正六面体的6个面着色可得不同的方案数 $M$ ，根据polya定理，
$M=\frac{1}{24}(m^6 + 6 \cdot m^3 + 3 \cdot m^4 + 6 \cdot m^3 + 8 \cdot m^2)$

例题：用2种颜色给正6面体的8个顶点着色，有多少种方案？

解：

WPS拼图0

不动置换(1)(2)(3)(4)(5)(6)(7)(8)，格式为 $1)^8$ ，只有1种。
绕x轴，旋转90度的置换为(1234)(5678)，旋转-90度的置换为(4321)(8765)，格式为 $4)^2$ ，正六面体对面有3对，故同类置换有6个。
绕x轴，旋转180度的置换为(13)(24)(57)(68)，格式为 $2)^4$ ，正六面体对面有3对，故同类置换有3个。
绕y轴，旋转180度的置换为(17)(35)(28)(46)，格式为 $2)^4$ ，正六面体有12条棱，6对棱，故同类置换有6个。
绕z轴，旋转120度的置换为(136)(2)(457)(8)，旋转-120度的置换为(631)(754)，格式为 $3)^2$ ，正六面体有4条对角线，故同类置换为8个。

根据polya定理，不同的着色方案为，
$M=\frac{1}{24}(2^8 + 6 \cdot 2^2 + 3 \cdot 2^4 + 6 \cdot 2^4 + 8 \cdot 2^4) \\ =\frac{1}{24}(256+24+48+96+128)=\frac{552}{24}=23$

例题：一个正6面体的6个面用g，r, b, y四种颜色涂染，求其中两个面用色g，两个面用色y, 其余一面用b, 一面用r的方案数。

解：再次看这个图

分类讨论	旋转方式	置换群	格式	同类置换个数
1	不动置换	(1)(2)(3)(4)(5)(6)	$1)^6$	1
2	绕AB旋转90度和-90度	(1)(2345)(6)和(1)(5432)(6)	$1)^2(4)$	2×3=6
3	绕AB旋转180度	(1)(24)(35)(6)	$1)^2(2)^2$	3
4	绕CD旋转180度	(16)(34)(25)	$2)^3$	6
5	绕EF旋转120度和-120度	(125)(346)和(521)(643)	$3)^2$	2×4=8

由母函数形式的polya定理可得
$L=\frac{1}{24}[(g+r+b+y)^6+6(g+r+b+y)^2(g^4+r^4+b^4+y^4)+3(g+r+b+y)^2(g^2+r^2+b^2+y^2)^2+6(g^2+r^2+b^2+y^2)^3+8(g^3+r^3+b^3+y^3)^2]$
所求方案数即 $g^2rby^2$ 的系数，故方案数为
$\frac{1}{24}(C_6^2C_4^2C_2^1C_1^1+3C_2^1C_1^1C_2^1C_1^1)=\frac{192}{24}=8$

例题：一个正八面体，用红蓝两色对6个顶点进行着色；用黄绿两种颜色对八个面进行染色，试求其中4个顶点为红色，两个顶点为蓝色，黄和绿的面各四面的方案数。

解：

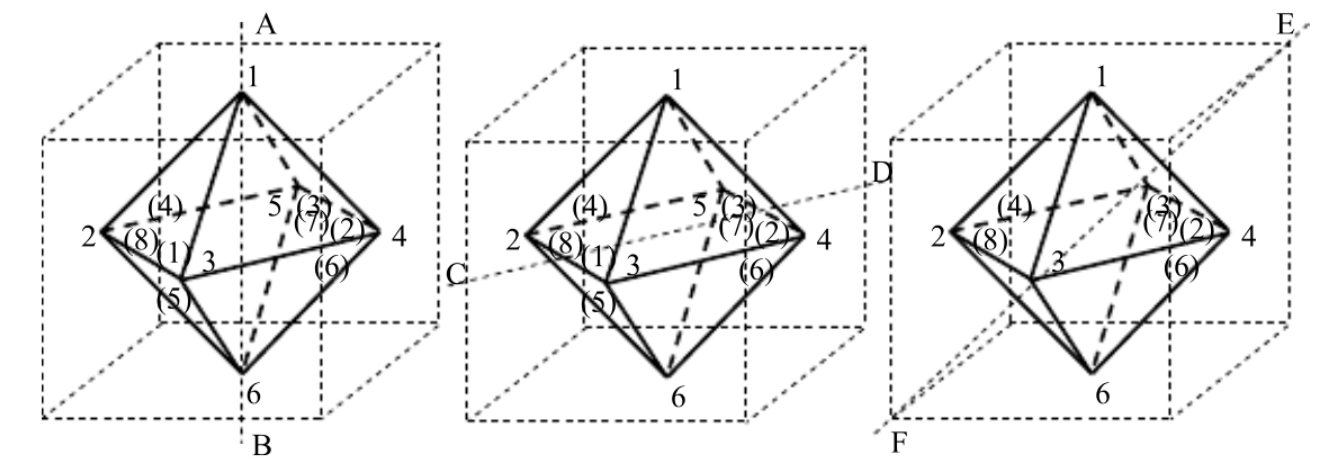
Untitled

分类讨论	旋转方式	格式	同类置换个数
1	不动置换	$1)^6$ - $1)^8$	1
2	绕AB旋转90度和-90度	$1)^2(4)$ - $4)^2$	2×3=6
3	绕AB旋转180度	$1)^2(2)^2$ - $2)^4$	3
4	绕CD旋转180度	$2)^3$ - $2)^4$	6
5	绕EF旋转120度和-120度	$3)^2$ - $1)^2(3)^2$	2×4=8

根据母函数形式的polya定理，染色方案枚举：
$P(r,b,y,g)=\frac{1}{24}[(r+b)^6(y+g)^8+6(r+b)^2(r^4+b^4)(y^4+g^4)^2+3(r+b)^2(r^2+b^2)^2(y^2+g^2)^4+6(r^2+b^2)^3(y^2+g^2)^4+8(r^3+b^3)^2(y+g)^2(y^3+g^3)^2]$
其中 $r^4b^2y^4g^4$ 的系数即为所求方案数：
$\frac{1}{24}[C_6^4C_2^2C_8^4C_4^4+6\cdot C_2^2C_1^1C_2^1C_1^1+3\cdot(C_2^2C_2^1+C_2^2C_2^2)C_4^2C_2^2+6\cdot C_3^2C_1^1C_4^2C_2^2+8\cdot0] =\frac{1}{24}[15\times70+6\times2+3\times(2+1)\times6+6\times3\times6+0] =\frac{1}{24}(1024+12+54+108) =\frac{1224}{24} =51$