原文链接: https://www.alanzucconi.com/2015/09/09/understanding-the-gaussian-distribution/
-
引言
考虑一下如何在一个平面上生成随机点。这些点可以代表敌人,树木,或者任何实例。在Unity中最简单的方式就是:
Vector3 position = new Vector3();
position.x = Random.Range(min,max),
position.y = Random.Range(min,max);
transform.position = position;用Random.Range就可以生成下图中蓝色盒子内的点了。这些点均匀地散布在平面内,使得整个平面点的密度一致。
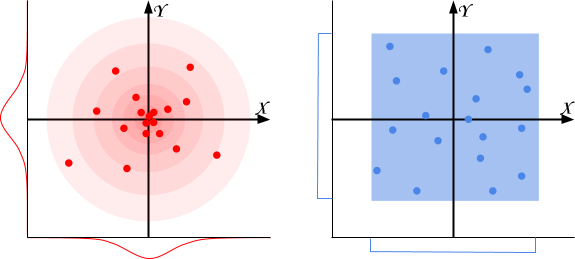
只是许多自然现象并不服从均匀分布,它们更像上图左边中的红点那样服从另一种概率分布:高斯分布。经验法则是:在自然场景中如果有某个值在一个确定的值附近徘徊,那么它很可能服从高斯分布。例如:
伤害:一个敌人,或者一把武器可造成的输出。
粒子密度:在某个特定物体附近的粒子的数目(火星子,灰尘等等)。
青草绿树:树与草在一个生态系统中的分布,例如一个湖边上植物的位置,或是一座山上石头的分布。
-
理解均匀分布
当你掷骰子时,掷出6点的概率是1/6。从概率学的角度上说,扔骰子就是从一个均匀的,离散的分布中采样一个值的过程,如下左图所示。每个均匀分布都能用一个n面骰子来表示。每个面x有着相同的被选中的概率:1/n。类似Random.Range的函数,返回的则是一个连续的,在一定范围之上的均匀分布,如下右图所示。
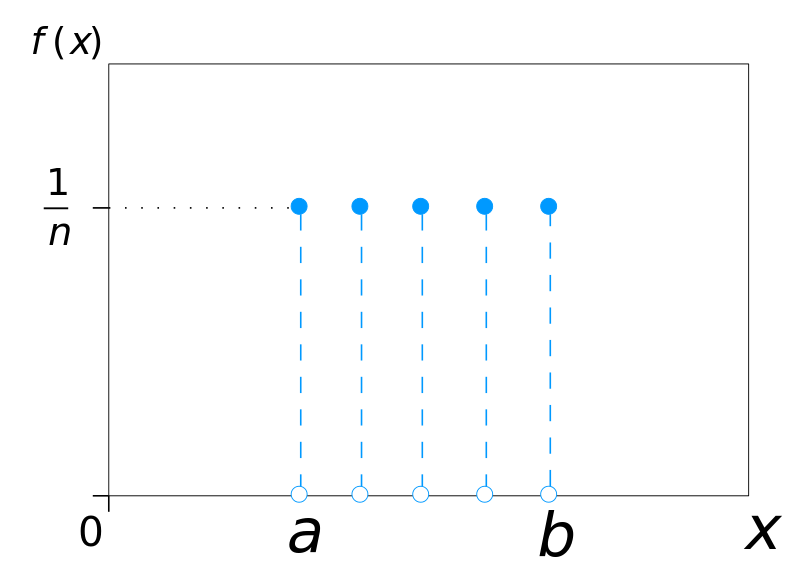
在许多案例中,均匀分布是一个好的选择。例如从一套卡组中随机选择一张卡就可以用其完美建模。
-
何为高斯分布
自然界中有许多现象不服从均匀分布。例如,当你测量一个屋子里人的身高时,你会发现有些值的出现次数要显著地高于其他值。大部分人身高相若,极高或极矮的人很罕见。随机从房间里选一个人,他的身高很可能与均值很接近。这些现象是典型的服从高斯(或正态)分布的。高斯分布中一个给定值的出现概率为:
均匀分布仅有一个参数n,而高斯分布则有两个参数和
,分别代表均值和方差。均值反映了概率曲线的中心位置所在,而方差则显示了某个服从该分布的随机值偏离均值的可能性。
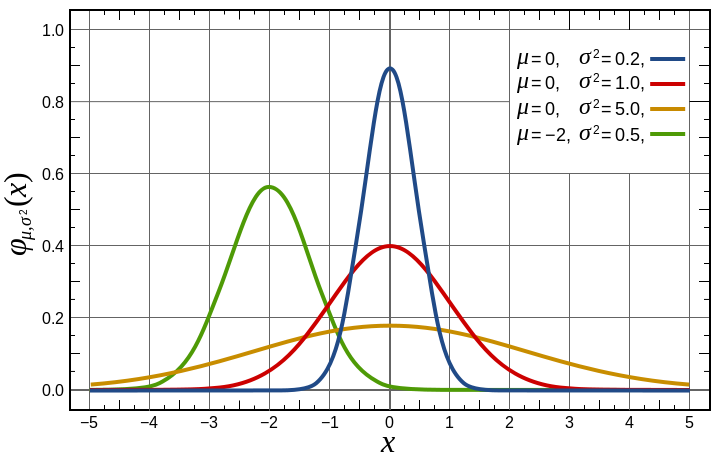
若某个变量X服从高斯分布,则可将其写作:
-
高斯分布示例
让人吃惊的是,高斯分布可以通过正态分布产生。尽管两者在表达式上大相径庭,却有着密切的联系。我们想象一下,有个酒鬼正在下图中走路:他从图的左侧中间点出发,每次往右走一步时,他以等概率往上/下走一步。在x步以后他最有可能走到哪儿去呢?
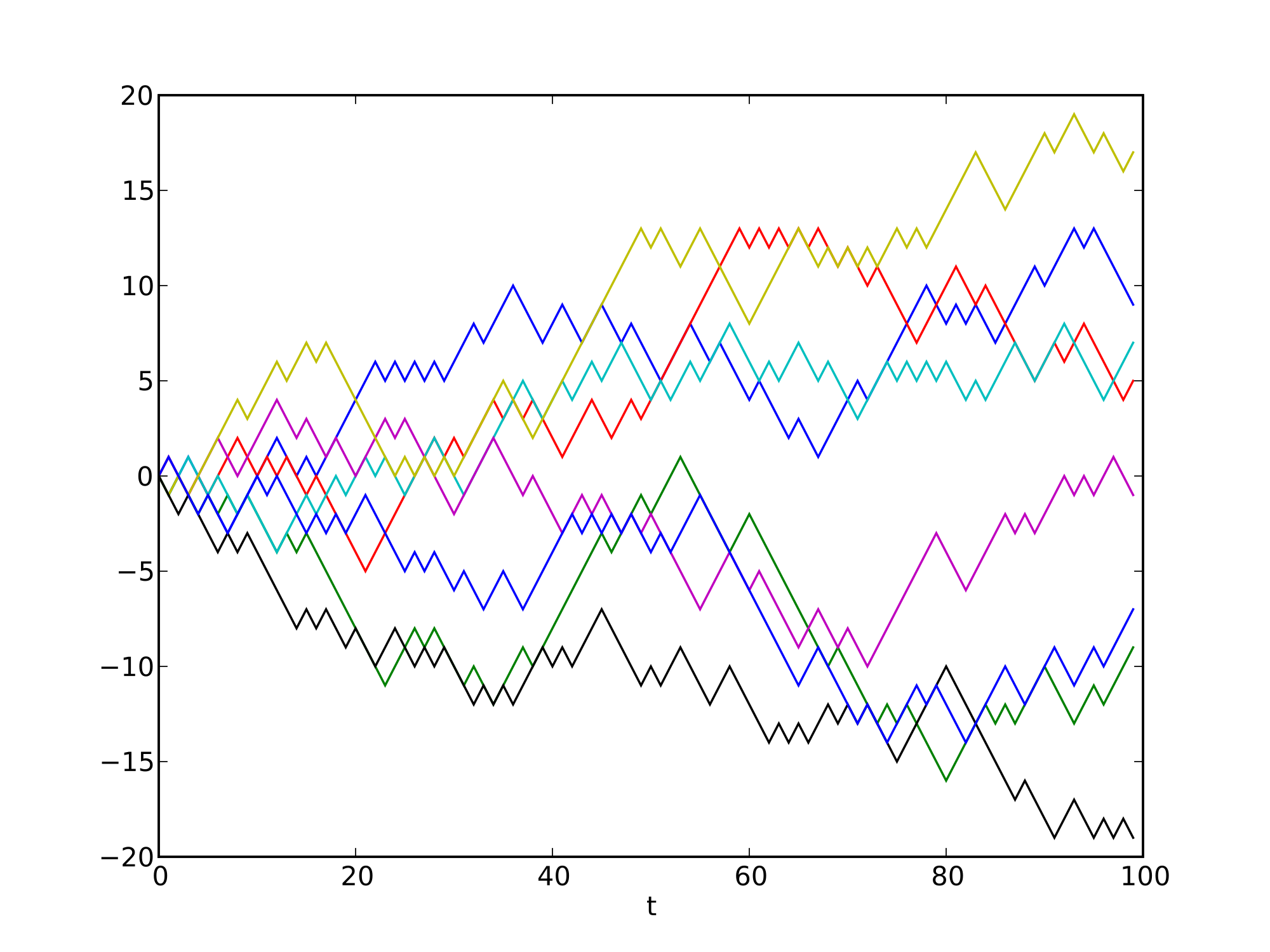
因为每步都是等概率的,所以上图所有的路径都是等概率发生的。然而越往两边的终点走,路线越少;越往中间走,路线越多。因此这个酒鬼最有可能待在离中心的终点附近。如果有足够多的酒鬼和足够的时间去走路,那么他们最终的位置计数图将很接近于高斯分布。
这个理论在19世纪被Francis Galton以bean machine实验验证过,如下图所示。这一实验背后隐藏着中心极限定理的思想:在自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的。

-
高斯分布推演
回头看看那个bean machine,想想每个球落入一个确定柱子里的概率是多少呢?
这就是所谓的二项分布。只是这个式子看上去一点也不“高斯分布”,怎么办呢?
令n趋近于无穷大,将离散的数值转为连续的——
首先,要将二项式系数扩展一下。这个式子由阶乘构成,而根据斯特林公式:
,该式可转换成:
,其中
,
。






















 1834
1834

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








