该博客探讨了硼原子的核外电子分布情况，详细列出了五个电子的主量子数、角量子数和磁量子数。根据这些量子数，进一步计算了硼原子的总能量，其中涉及了动能和势能的求和。最后，通过特定的函数计算得到能量值为-29.1，并引用了徐光宪的《量子化学》作为理论依据。
设B原子核外5个电子的轨道分别是
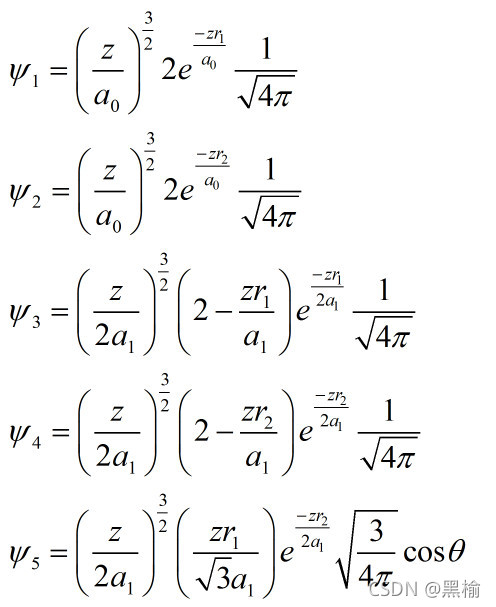
这5个电子的主，角，磁量子数分别是(1,0,0), (1,0,0), (2,0,0), (2,0,0), (2,1,0).
硼原子的能量为
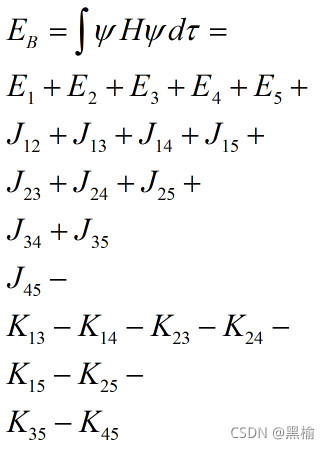
其中E1=E2，E3=E4，
J13=J14=J23=J24，J15=J25，J34=J45，
K13=K14=K23=K24，k15=K25，K35=K45
因此
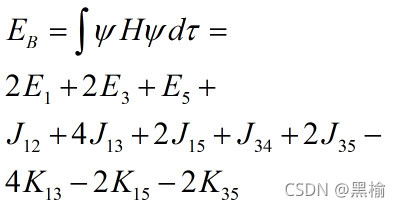
其中动能+势能为
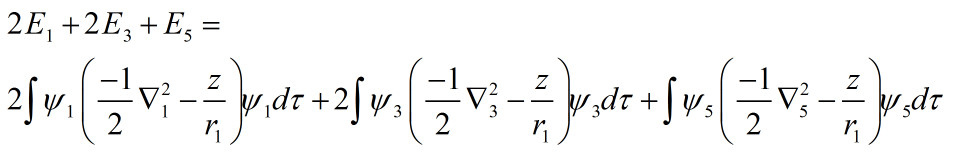
=2*（-12.5）+2*（-1.367）-1.367=-29.1
因此
double fh=hin(fx1,fx1)*2+hin(fx2,fx2)*2+hin(fx3,fx3);
fh=-29.1
*徐光宪《量子化学》
扫一扫
535
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
