二叉树问题全集OK

最新推荐文章于 2021-04-28 02:15:33 发布

gexiaobaoHelloWorld

最新推荐文章于 2021-04-28 02:15:33 发布

阅读量1.2k

点赞数

分类专栏：算法设计

本文链接：https://blog.csdn.net/gexiaobaoHelloWorld/article/details/10715967

版权

算法设计专栏收录该内容

14 篇文章 0 订阅

订阅专栏

http://blog.csdn.net/luckyxiaoqiang/article/details/7518888

二叉树是递归定义的，因此，与二叉树有关的题目基本都可以用递归思想解决，当然有些题目非递归解法也应该掌握，如非递归遍历节点等等。

1，二叉树节点定义

struct BinaryTreeNode
{
    int m_nValue;
    BinaryTreeNode* m_pLeft;
    BinaryTreeNode* m_pRight;
};

2，求二叉树中的节点个数

递归解法：
（1）如果二叉树为空，节点个数为0
（2）如果二叉树不为空，二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1
参考代码如下：

int GetNodeNum(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL) // 递归出口
		return 0;
	return GetNodeNum(pRoot->m_pLeft) + GetNodeNum(pRoot->m_pRight) + 1;
}

3，求二叉树的深度

递归解法：
（1）如果二叉树为空，二叉树的深度为0
（2）如果二叉树不为空，二叉树的深度 = max(左子树深度，右子树深度) + 1
参考代码如下：

int GetDepth(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL) // 递归出口
		return 0;
	int depthLeft = GetDepth(pRoot->m_pLeft);
	int depthRight = GetDepth(pRoot->m_pRight);
	return depthLeft > depthRight ? (depthLeft + 1) : (depthRight + 1); 
}

4，前序遍历，中序遍历，后序遍历

前序遍历递归解法：
（1）如果二叉树为空，空操作
（2）如果二叉树不为空，访问根节点，前序遍历左子树，前序遍历右子树
参考代码如下：

4.1 前序遍历（递归版）

void PreOrderTraverse(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL)
		return;
	Visit(pRoot); // 访问根节点
	PreOrderTraverse(pRoot->m_pLeft); // 前序遍历左子树
	PreOrderTraverse(pRoot->m_pRight); // 前序遍历右子树
}

4.2 中序遍历（递归版）

void InOrderTraverse(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL)
		return;
	InOrderTraverse(pRoot->m_pLeft); // 中序遍历左子树
	Visit(pRoot); // 访问根节点
	InOrderTraverse(pRoot->m_pRight); // 中序遍历右子树
}

4.3 后序遍历（递归版）

void PostOrderTraverse(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL)
		return;
	PostOrderTraverse(pRoot->m_pLeft); // 后序遍历左子树
	PostOrderTraverse(pRoot->m_pRight); // 后序遍历右子树
	Visit(pRoot); // 访问根节点
}

4.4 前序遍历（非递归版）

http://www.slyar.com/blog/bitree-unrecursion-c.html

前序遍历:先访问根节点，再访问左子树，最后访问右子树。设置一个栈，出栈即为访问节点。先将根节点进栈，在栈不空时一直如下循环:出栈，访问，将其右孩子进栈，再将左孩子进栈。

void PreOrderNoRecusion(BTNode* root)
{
    Stack<BTNode*> bTStack;
    BTNode* p;
    if (root != NULL)
    {
        /* 根节点入栈 */
        bTStack.push(root);
        /* 栈不空时循环 */
        while (!bTStack.empty())
        {
            /* 出栈并访问该节点 */
            p = bTStack.top();
            bTStack.pop();
            visit(p);
            /* 右孩子入栈 */
            if (p->rchild != NULL)
            {
                bTStack.push(p->rchild);
            }
            /* 左孩子入栈 */
            if (p->lchild != NULL)
            {
                bTStack.push(p->lchild);
            }
        }
    }
}

4.5 中序遍历（非递归版）

中序遍历:先访问左子树，再访问根节点，最后访问右子树。设置一个栈，出栈即为访问节点。先将根节点的左节点全部进栈，然后出栈一个节点，访问。将该节点的右孩子节点进栈，再将右孩子节点的所有左节点全部进栈...如此这般直到栈空为止。

/* 非递归中序遍历二叉树 */
void InOrderNoRecusion(BTNode* root)
{
    Stack<BTNode*> bTStack;
    BTNode* p;
    if (root != NULL)
    {
        p = root;
        while (!bTStack.empty() || p != NULL)
        {
            /* 扫描p的所有左节点并入栈 */
            while (p != NULL)
            {
                bTStack.push(p);
                p = p->lchild;
            }
            /* 访问左节点 */
            if (!bTStack.empty())
            {
                /* 出栈并访问该节点 */
                p = bTStack.top();
                bTStack.pop();
                visit(p);
                /* 扫描p的右孩子 */
                p = p->rchild;
            }
        }
    }
}

4.6 后序遍历（非递归版）？？？

5，层次遍历二叉树（按层次从上往下，从左往右）

相当于广度优先搜索，使用队列实现。队列初始化，将根节点压入队列。当队列不为空，进行如下操作：弹出一个节点，访问，若左子节点或右子节点不为空，将其压入队列。

void LevelTraverse(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL)
		return;
	queue<BinaryTreeNode *> q;
	q.push(pRoot);
	while(!q.empty())
	{
		BinaryTreeNode * pNode = q.front();
		q.pop();
		Visit(pNode); // 访问节点
		if(pNode->m_pLeft != NULL)
			q.push(pNode->m_pLeft);
		if(pNode->m_pRight != NULL)
			q.push(pNode->m_pRight);
	}
	return;
}

6，将二叉查找树变为有序的双向链表

要求不能创建新节点，只调整指针。
递归解法：
（1）如果二叉树查找树为空，不需要转换，对应双向链表的第一个节点是NULL，最后一个节点是NULL
（2）如果二叉查找树不为空：
如果左子树为空，对应双向有序链表的第一个节点是根节点，左边不需要其他操作；
如果左子树不为空，转换左子树，二叉查找树对应双向有序链表的第一个节点就是左子树转换后双向有序链表的第一个节点，同时将根节点和左子树转换后的双向有序链表的最后一个节点连接；
如果右子树为空，对应双向有序链表的最后一个节点是根节点，右边不需要其他操作；
如果右子树不为空，对应双向有序链表的最后一个节点就是右子树转换后双向有序链表的最后一个节点，同时将根节点和右子树转换后的双向有序链表的第一个节点连接。
参考代码如下：

/******************************************************************************
参数：
pRoot: 二叉查找树根节点指针
pFirstNode: 转换后双向有序链表的第一个节点指针
pLastNode: 转换后双向有序链表的最后一个节点指针
******************************************************************************/
void Convert(BinaryTreeNode * pRoot, 
             BinaryTreeNode * & pFirstNode, BinaryTreeNode * & pLastNode)
{
	BinaryTreeNode *pFirstLeft, *pLastLeft, * pFirstRight, *pLastRight;
	if(pRoot == NULL) 
	{
		pFirstNode = NULL;
		pLastNode = NULL;
		return;
	}

	if(pRoot->m_pLeft == NULL)
	{
		// 如果左子树为空，对应双向有序链表的第一个节点是根节点
		pFirstNode = pRoot;
	}
	else
	{
		Convert(pRoot->m_pLeft, pFirstLeft, pLastLeft);
		// 二叉查找树对应双向有序链表的第一个节点就是左子树转换后双向有序链表的第一个节点
		pFirstNode = pFirstLeft;
		// 将根节点和左子树转换后的双向有序链表的最后一个节点连接
		pRoot->m_pLeft = pLastLeft;
		pLastLeft->m_pRight = pRoot;
	}

	if(pRoot->m_pRight == NULL)
	{
		// 对应双向有序链表的最后一个节点是根节点
		pLastNode = pRoot;
	}
	else
	{
		Convert(pRoot->m_pRight, pFirstRight, pLastRight);
		// 对应双向有序链表的最后一个节点就是右子树转换后双向有序链表的最后一个节点
		pLastNode = pLastRight;
		// 将根节点和右子树转换后的双向有序链表的第一个节点连接
		pRoot->m_pRight = pFirstRight;
		pFirstRight->m_pLeft = pRoot;
	}

	return;
}

或者：

/******************************************************************************
参数：
pRoot: 二叉查找树根节点指针
pFirstNode: 转换后双向有序链表的第一个节点指针
pLastNode: 转换后双向有序链表的最后一个节点指针
******************************************************************************/
void Convert(BinaryTreeNode * pRoot, 
             BinaryTreeNode * & pFirstNode, BinaryTreeNode * & pLastNode)
{
	if(pRoot == NULL) 
	{
		pFirstNode = NULL;
		pLastNode = NULL;
		return;
	}

	BinaryTreeNode * pLeftTail, * pRightHead;
	Convert(pFirstNode,pLeftTail,pRoot->m_pLeft);
	Convert(pRightHead,pLastNode,pRoot->m_pRight);

	if(pLeftTail == NULL){
		pFirstNode = pRoot;
	}
	else{
		pLeftTail->m_pRight = pRoot;
		pRoot->m_pLeft = pLeftTail;
	}

	if(pRightHead == NULL){
		pLastNode = pRoot;
	}
	else{
		pRightHead->m_pLeft = pRoot;
		pRoot->m_pRight = pRightHead;
	}

	return;
}

7，求二叉树第K层的节点个数

递归解法：
（1）如果二叉树为空，返回0
（2）如果二叉树不为空，k<1返回0
（3）如果二叉树不为空，k==1，返回1
（4）如果二叉树不为空，k>1，返回左子树中k-1层的节点个数与右子树k-1层节点个数之和
参考代码如下：

int GetNodeNumKthLevel(BinaryTreeNode * pRoot, int k)
{
	if(pRoot == NULL || k < 1)
		return 0;
	if(k == 1)
		return 1;
	int numLeft = GetNodeNumKthLevel(pRoot->m_pLeft, k-1); // 左子树中k-1层的节点个数
	int numRight = GetNodeNumKthLevel(pRoot->m_pRight, k-1); // 右子树中k-1层的节点个数
	return (numLeft + numRight);
}

8，求二叉树中叶子节点的个数

递归解法：
（1）如果二叉树为空，返回0
（2）如果二叉树不为空且左右子树为空，返回1
（3）如果二叉树不为空，且左右子树不同时为空，返回左子树中叶子节点个数加上右子树中叶子节点个数
参考代码如下：

int GetLeafNodeNum(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL)
		return 0;
	if(pRoot->m_pLeft == NULL && pRoot->m_pRight == NULL)
		return 1;
	int numLeft = GetLeafNodeNum(pRoot->m_pLeft); // 左子树中叶节点的个数
	int numRight = GetLeafNodeNum(pRoot->m_pRight); // 右子树中叶节点的个数
	return (numLeft + numRight);
}

9，判断两棵二叉树是否结构相同

不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
递归解法：
（1）如果两棵二叉树都为空，返回真
（2）如果两棵二叉树一棵为空，另一棵不为空，返回假
（3）如果两棵二叉树都不为空，如果对应的左子树和右子树都同构返回真，其他返回假
参考代码如下：

bool StructureCmp(BinaryTreeNode * pRoot1, BinaryTreeNode * pRoot2)
{
	if(pRoot1 == NULL && pRoot2 == NULL) // 都为空，返回真
		return true;
	else if(pRoot1 == NULL || pRoot2 == NULL) // 有一个为空，一个不为空，返回假
		return false;
	bool resultLeft = StructureCmp(pRoot1->m_pLeft, pRoot2->m_pLeft); // 比较对应左子树 
	bool resultRight = StructureCmp(pRoot1->m_pRight, pRoot2->m_pRight); // 比较对应右子树
	return (resultLeft && resultRight);
}

10，判断二叉树是不是平衡二叉树

递归解法：
（1）如果二叉树为空，返回真
（2）如果二叉树不为空，如果左子树和右子树都是AVL树并且左子树和右子树高度相差不大于1，返回真，其他返回假
参考代码：

bool IsAVL(BinaryTreeNode * pRoot, int & height)
{
	if(pRoot == NULL) // 空树，返回真
	{
		height = 0;
		return true;
	}
	int heightLeft;
	bool resultLeft = IsAVL(pRoot->m_pLeft, heightLeft);
	int heightRight;
	bool resultRight = IsAVL(pRoot->m_pRight, heightRight);

	height = max(heightLeft, heightRight) + 1;

	if(resultLeft && resultRight && abs(heightLeft - heightRight) <= 1) // 左子树和右子树都是AVL，并且高度相差不大于1，返回真
		return true;
	else
		return false;
}

11，求二叉树的镜像

递归解法：
（1）如果二叉树为空，返回空
（2）如果二叉树不为空，求左子树和右子树的镜像，然后交换左子树和右子树
参考代码如下：

BinaryTreeNode * Mirror(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL) // 返回NULL
		return NULL;
	BinaryTreeNode * pLeft = Mirror(pRoot->m_pLeft); // 求左子树镜像
	BinaryTreeNode * pRight = Mirror(pRoot->m_pRight); // 求右子树镜像
        // 交换左子树和右子树
	pRoot->m_pLeft = pRight;
	pRoot->m_pRight = pLeft;
	return pRoot;
}

12，由前序遍历序列和中序遍历序列重建二叉树

二叉树前序遍历序列中，第一个元素总是树的根节点的值。中序遍历序列中，左子树的节点的值位于根节点的值的左边，右子树的节点的值位
于根节点的值的右边。
递归解法：
（1）如果前序遍历为空或中序遍历为空或节点个数小于等于0，返回NULL。
（2）创建根节点。前序遍历的第一个数据就是根节点的数据，在中序遍历中找到根节点的位置，可分别得知左子树和右子树的前序和中序遍
历序列，重建左右子树。

BinaryTreeNode * RebuildBinaryTree(int* pPreOrder, int* pInOrder, int nodeNum)
{
	if(pPreOrder == NULL || pInOrder == NULL || nodeNum <= 0)
		return NULL;
	BinaryTreeNode * pRoot = new BinaryTreeNode;
	// 前序遍历的第一个数据就是根节点数据
	pRoot->m_nValue = pPreOrder[0];
	pRoot->m_pLeft = NULL;
	pRoot->m_pRight = NULL;
	// 查找根节点在中序遍历中的位置，中序遍历中，根节点左边为左子树，右边为右子树
	int rootPositionInOrder = -1;
	for(int i = 0; i < nodeNum; i++)
		if(pInOrder[i] == pRoot->m_nValue)
		{
			rootPositionInOrder = i;
			break;
		}
	if(rootPositionInOrder == -1)
	{
		throw std::exception("Invalid input.");
	}
	// 重建左子树
	int nodeNumLeft = rootPositionInOrder;
	int * pPreOrderLeft = pPreOrder + 1;
	int * pInOrderLeft = pInOrder;
	pRoot->m_pLeft = RebuildBinaryTree(pPreOrderLeft, pInOrderLeft, nodeNumLeft);
	// 重建右子树
	int nodeNumRight = nodeNum - nodeNumLeft - 1;
	int * pPreOrderRight = pPreOrder + 1 + nodeNumLeft;
	int * pInOrderRight = pInOrder + nodeNumLeft + 1;
	pRoot->m_pRight = RebuildBinaryTree(pPreOrderRight, pInOrderRight, nodeNumRight);
	return pRoot;
}

同样，有中序遍历序列和后序遍历序列，类似的方法可重建二叉树，但前序遍历序列和后序遍历序列不同恢复一棵二叉树，证明略。

13，判断二叉树是不是完全二叉树

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全
二叉树。
有如下算法，按层次（从上到下，从左到右）遍历二叉树，当遇到一个节点的左子树为空时，则该节点右子树必须为空，且后面遍历的节点左
右子树都必须为空，否则不是完全二叉树。

bool IsCompleteBinaryTree(BinaryTreeNode * pRoot)
{
	if(pRoot == NULL) //空树是否是完全二叉树有待确定
		return false;
	queue<BinaryTreeNode *> q;
	q.push(pRoot);
	bool mustHaveNoChild = false;
	bool result = true;
	while(!q.empty())
	{
		BinaryTreeNode * pNode = q.front();
		q.pop();
		if(mustHaveNoChild) // 已经出现了有空子树的节点了，后面出现的必须为叶节点（左右子树都为空）
		{
			if(pNode->m_pLeft != NULL || pNode->m_pRight != NULL)
			{
				result = false;
				break;
			}
		}
		else  //处理当前节点
		{ 
                        //当前节点的【左非空，右非空】    
			if(pNode->m_pLeft != NULL && pNode->m_pRight != NULL)
			{
				q.push(pNode->m_pLeft);
				q.push(pNode->m_pRight);
			}
                        //当前节点的【左非空，右空】
			else if(pNode->m_pLeft != NULL && pNode->m_pRight == NULL)
			{
				mustHaveNoChild = true;
				q.push(pNode->m_pLeft);
			}
                        //当前节点的【左空，右非空】
			else if(pNode->m_pLeft == NULL && pNode->m_pRight != NULL)
			{
				result = false;
				break;
			}
                        //当前节点的【左空，右空】
			else
			{
				mustHaveNoChild = true;
			}
		}
	}
	return result;
}

14，求二叉树中两个节点的最低公共祖先节点

递归解法：
（1）如果两个节点分别在根节点的左子树和右子树，则返回根节点
（2）如果两个节点都在左子树，则递归处理左子树；如果两个节点都在右子树，则递归处理右子树
参考代码如下：

bool FindNode(BinaryTreeNode * pRoot, BinaryTreeNode * pNode)
{
	if(pRoot == NULL || pNode == NULL)
		return false;

	if(pRoot == pNode)
		return true;

	bool found = FindNode(pRoot->m_pLeft, pNode);
	if(!found)
		found = FindNode(pRoot->m_pRight, pNode);

	return found;
}

BinaryTreeNode * GetLastCommonParent(BinaryTreeNode * pRoot, 
                                     BinaryTreeNode * pNode1, 
                                     BinaryTreeNode * pNode2){
        //pNode1在左子树  
	if(FindNode(pRoot->m_pLeft, pNode1))
	{
                //pNode2在右子树
		if(FindNode(pRoot->m_pRight, pNode2))
			return pRoot;
                //pNode2在左子树
		else
			return GetLastCommonParent(pRoot->m_pLeft, pNode1, pNode2);
	}
        //pNode1在右子树
	else
	{
                //pNode2在左子树
		if(FindNode(pRoot->m_pLeft, pNode2))
			return pRoot;
                //pNode2在右子树
		else
			return GetLastCommonParent(pRoot->m_pRight, pNode1, pNode2);
	}
}

递归解法效率很低，有很多重复的遍历，下面看一下非递归解法。
非递归解法：
先求从根节点到两个节点的路径，然后再比较对应路径的节点就行，最后一个相同的节点也就是他们在二叉树中的最低公共祖先节点
参考代码如下：

bool GetNodePath(BinaryTreeNode * pRoot, BinaryTreeNode * pNode, 
                 list<BinaryTreeNode *> & path)
{
	if(pRoot == pNode)
	{	
		path.push_back(pRoot);
		return true;
	}
	if(pRoot == NULL)
		return false;
	path.push_back(pRoot);
	bool found = false;
	found = GetNodePath(pRoot->m_pLeft, pNode, path);
	if(!found)
		found = GetNodePath(pRoot->m_pRight, pNode, path);
	if(!found)
		path.pop_back();
	return found;
}
BinaryTreeNode * GetLastCommonParent(BinaryTreeNode * pRoot, BinaryTreeNode * pNode1, BinaryTreeNode * pNode2)
{
	if(pRoot == NULL || pNode1 == NULL || pNode2 == NULL)
		return NULL;
	list<BinaryTreeNode*> path1;
	bool bResult1 = GetNodePath(pRoot, pNode1, path1);
	list<BinaryTreeNode*> path2;
	bool bResult2 = GetNodePath(pRoot, pNode2, path2);
	if(!bResult1 || !bResult2) 
		return NULL;
	BinaryTreeNode * pLast = NULL;
	list<BinaryTreeNode*>::const_iterator iter1 = path1.begin();
	list<BinaryTreeNode*>::const_iterator iter2 = path2.begin();
	while(iter1 != path1.end() && iter2 != path2.end())
	{
		if(*iter1 == *iter2)
			pLast = *iter1;
		else
			break;
		iter1++;
		iter2++;
	}
	return pLast;
}

在上述算法的基础上稍加变化即可求二叉树中任意两个节点的距离了。

15，求二叉树中节点的最大距离

即二叉树中相距最远的两个节点之间的距离。
递归解法：
（1）如果二叉树为空，返回0，同时记录左子树和右子树的深度，都为0
（2）如果二叉树不为空，最大距离要么是左子树中的最大距离，要么是右子树中的最大距离，要么是左子树节点中到根节点的最大距离+右子树节点中到根节点的最大距离，同时记录左子树和右子树节点中到根节点的最大距离。

这个更简单：

/*
 * 计算树高
 */
int get_depth(Tree *tree) {
    int depth = 0;
    if ( tree ) {
        int a = get_depth(tree->left);
        int b = get_depth(tree->right);
        depth = ( a > b ) ? (a+1) : (b+1);
    }
    return depth;
}

/*
 * 树间节点的最大距离
 */
int get_max_distance(Tree *tree) {
    int distance = 0;
    if ( tree ) {
        //1，左子树节点中到根节点的最大距离+右子树节点中到根节点的最大距离
        distance = get_depth(tree->left) + get_depth(tree->right);
        //2，左子树中节点间最大距离
        int l_distance = get_max_distance(tree->left);
		//3，右子树节点间最大距离
        int r_distance = get_max_distance(tree->right);

        distance = ( l_distance > distance ) ? l_distance : distance;
        distance = ( r_distance > distance ) ? r_distance : distance;
    }
    return distance;
}

解法2：

int GetMaxDistance(BinaryTreeNode * pRoot, int & maxLeft, int & maxRight)
{
	// maxLeft, 左子树中的节点距离根节点的最远距离
	// maxRight, 右子树中的节点距离根节点的最远距离
        // return int，二叉树节点最大距离
	if(pRoot == NULL)
	{
		maxLeft = 0;
		maxRight = 0;
		return 0;
	}
	int maxLL, maxLR, maxRL, maxRR;
	int maxDistLeft, maxDistRight;

	//左子树非空，计算maxLeft
	if(pRoot->m_pLeft != NULL)
	{
		maxDistLeft = GetMaxDistance(pRoot->m_pLeft, maxLL, maxLR);
		maxLeft = max(maxLL, maxLR) + 1;
	}
        //左子树空
	else
	{
		maxDistLeft = 0;
		maxLeft = 0;
	}

	//右子树非空，计算maxRight
	if(pRoot->m_pRight != NULL)
	{
		maxDistRight = GetMaxDistance(pRoot->m_pRight, maxRL, maxRR);
		maxRight = max(maxRL, maxRR) + 1;
	}
        //右子树空
	else
	{
		maxDistRight = 0;
		maxRight = 0;
	}

        //最大距离要么是左子树中的最大距离，要么是右子树中的最大距离，要么是左子树节点中到根节点的最大距离+右子树节点中到根节点的最大距离
	return max(max(maxDistLeft, maxDistRight), maxLeft+maxRight);
}

16，求二叉树中和为某值的所有路径

题目：输入一个整数和一棵二元树。从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。打印出和与输入整数相等的所有路径。
例如输入整数22 和如下二元树

10
| \
5 12
| \
4 7

则打印出两条路径：10, 12 和10, 5, 7。

思路：回溯+递归（使用一个栈来帮助回溯）

struct TreeNode { 
	int data; 
	TreeNode * left; 
	TreeNode * right; 
}; 
 
void printPaths(TreeNode * root, int sum) { 
	int path[MAX_HEIGHT]; //记录路径的栈
	helper(root, sum, path, 0); //最初栈顶为0
} 
 
void helper(TreeNode * root, int sum, int path[], int top) { 
	//正向
	path[top++] = root.data; 
	sum -= root.data; 
	
	//终止条件是叶子节点
	if (root->left == NULL && root->right == NULL) { 	
		//要么打印
		if (sum == 0) printPath(path, top); 
		//要么回溯
		//else
	} else { 
		if (root->left != NULL) 
			helper(root->left, sum, path, top); 
		if (root->right != NULL) 
			helper(root->right, sum, path, top); 
	} 

	//回溯
	top--; 
	sum += root.data;    
}

17，判断整数序列是不是二元查找树的后序遍历结果

题目：输入一个整数数组，判断该数组是不是某二元查找树的后序遍历的结果。如果是返回true，否则返回false。

这样的树，其后续遍历序列为5、7、6、9、11、10、8

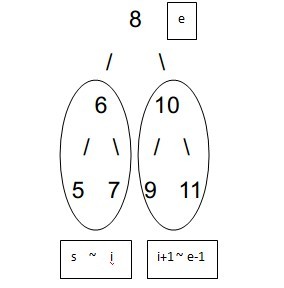
思路：这里使用递归的方法，将这棵树区分为左子树，右子树，根。这样就可以递归的进行判断。即（5,7,6）,（9,11,10）,（8）三部分。

int isPostorderResult(int a[], int n) { 
	return helper(a, 0, n-1); 
} 

int helper(int a[], int s, int e) { 
	if (e==s) return 1; 
	//找到左子树最后一个点i
	int i=e-1; 
	while (a[i]<a[e] && i>=s) 
		i--; 

	return (helper(a, s, i-1)&&helper(a, i+1, e-1)) 
}

18，判断一棵树是不是排序二叉树

boolean isSorted(BinaryTreeNode * pRoot){
 	if(pRoot == NULL)
 		return true;
 	//pRoot!=NULL
 	if(pRoot->m_pLeft != NULL && pRoot->m_pLeft->m_nValue > pRoot->m_nValue)
 		return false;
 	if(pRoot->m_pRight != NULL && pRoot->m_pRight->m_nValue < pRoot->m_nValue)
 		return false;
 	
 	return isSorted(pRoot->m_pLeft)&&isSorted(pRoot->m_pRight);
 }

18，排序二叉树，交换两个节点，如何检测？？？