作者:相国大人
写这篇博文用了很多时间和精力,如果这篇博文对你有帮助,希望您可以打赏给博主相国大人。哪怕只捐1毛钱,也是一种心意。通过这样的方式,也可以培养整个行业的知识产权意识。我可以和您建立更多的联系,并且在相关领域提供给您更多的资料和技术支持。
手机扫一扫,即可:
1. 导读
卷积神经网络CNN常用于处理具有栅格拓扑特征的数据。时间序列数据可以看做是在固定时间间隔采样的一维网格数据;图像可以看做是由像素组成的一个二维网格。在实际应用中,具有很好的效果。也是进入深度学习领域需要掌握的最基本的网络模型。卷积网络使用卷积来代替一般的矩阵乘法。将一层卷积结果作为一个输出层。
本文是一之后系列博文的第一篇。在本系列博文中,我们会全方位,足够深入的为你讲解CNN的知识。包括很多你之前在网上找了很多资料也没搞清楚的东西,例如:
1. 我们会全面深入的介绍卷积的概念,让你不仅仅知道卷积的运算,还能够从理性和感性的双重角度,理解卷积的意义。我们还会探讨为什么要使用卷积网络,卷积网络究竟有什么特性。
2. 我们会详细介绍池化的概念,并且告诉你为什么要做池化操作,池化操作究竟有什么特别的好处。
3. 我们会全面介绍CNN的各种形式。如:standard convolution,valid convolution, same convolution,full convolution,unshared convolution,tiled convolution等等。尤其是tiled convolution我们会用最能够让人理解的方式,让你透彻明白其中的原理。这一点,我们的工作要比网上其他博文做得更好。
4. 我们还将详细探讨卷积与矩阵乘法的关系。这一点,我们的工作也要比网上其他博文作的好。
5. 除此之外,我们还会探讨更多,更深入的知识,例如:CNN中的其他操作(如反卷积等),如何在数据集上使用不同维度的卷积,使得卷积操作更高效的方式 ,使用tensorflow进行CNN的实现,讨论并实现如何使用CNN做中文文本分类。
所有这些精彩的内容,都会在我接下来的博文中一一介绍。
因此,与网上其他博文相比,我们的工作更好,主要体现在:
1.对理论的介绍足够深入易懂
2. 我们会利用CNN做文本分类的实践。
3. 我们会绘制大量精美的示意图。保证博文的高质量和美观。
接下来,我们为大家介绍卷积的概念
2. 卷积
假如我们现在要追踪一艘船的位置,这艘船会给我们返回当前时刻
t
的它的位置坐标
我们把上面这个操作,叫做 卷积(convolution).常常简写为:

在我们这个场景(追踪船位置)中,我们的函数
ω
是权重函数,因此,它在全域上的积分和应该为1,并且是非负函数。因此这个
ω
函数,实质上就是一个概率密度函数。并且
ω(t)=0,if:t<0
,否则这意味着我们可以看到未来的数据,这不符合此场景下的逻辑。
但事实上,刚才说到的这两个限制,仅仅是在我们这个场景中是成立的。对于一般的卷积定义来说,不管
ω
是什么样的函数,只要可以写成公式
(2.1,2.2)
的形式,我们都称之为卷积操作。
特别的,在深度学习领域中,我们把公式
(2.1,2.2)
中的
x
叫做输入(input),把
在刚才的场景中,我们默认
在机器学习领域中,我们的input往往是多维数组,kernel也是由学习参数构成的多维数组。这样以来,我们可以把这些多维数组看做是张量。从公式
(2.3)
中可以看到,我们需要对无穷多数据进行求和,但实际上,如果我们假定,除了我们存储的观测值之外,其他没有观测到的值,统统记为0,那么就可以通过有限次的求和来得到式
(2.3)
的结果。
由上面的论述,我们知道,我们需要同时在多个维度上进行卷积操作。例如,如果我们使用二维图像
I
作为输入,那么我们也希望使用二维的kernel
对于卷积操作而言,交换 I 和
在CNN中, K 的尺寸一般要比
有趣的是,在很多机器学习库中,它们往往把上面公式的kernel进行“翻转”,得到下面的样子:
并且,也把这个叫做卷积(实际上应该叫做互相关)。
下图所示是运用公式 (2.5) 对Input中标有颜色的数据进行卷积的示意图。对于Input中白色数据,我们这里没有做,实际上,我们可以在Input外面补充相应数量的0值,来同样完成卷积。

卷积与普通的矩阵乘法相比,对应的连接更稀疏:

上面这张图表示的是两个神经网络。其中,左侧的神经网络是通过卷积得到的。 s 为featrure map,
右侧的网络是通过矩阵乘法得到的,具体来说,有 S=KX ,其中 K 就是网络中,这些边的权值。
从这两个图我们可以看到,由于kernel的规模一般远小于input,因此最后得到的网络是稀疏的。也就是说在所有的输出中,只有三个(
同样的,也可以反过来看:

在左侧的卷积网络中,只有3个输入可以影响输入,而在右侧的矩阵乘法网络中,所有的输入都会影响输出。
3. 在神经网络中使用卷积的原因
使用卷积的原因在于,它利用sparse interactions, parameter sharing, 和equivariant representations来提高机器学习系统。本小节的目的,就是分别介绍这三个特性。
3.1 sparse interactions
sparse interactions又叫做sparse connectivity 或sparse weights
关于这一点,我们在上一节的末尾,已经为大家讲到了。因此此处不再赘述。
需要说明的一点是,随着网络层数的增加,输出结点的输入域将会扩大,如下图:

在上面这张图中,更深层中节点的接受域要比浅层节点更大。这意味着,尽管直接连接比较稀疏,深层中的节点仍然可以获取大多数,甚至全部的输入节点的信息。
3.2 parameter sharing
在CNN中,kernel(也就是我们之前说的函数
ω
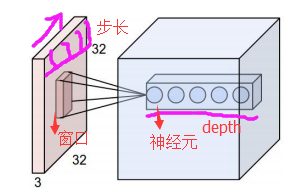
带着一组固定权重的神经元)对局部输入数据进行卷积计算。每计算完一个数据窗口内的局部数据后,数据窗口不断平移滑动,直到计算完所有数据。这个过程中,有这么几个参数:
a. 深度depth:神经元个数,决定输出的depth厚度。同时代表kernel个数。
b. 步长stride:决定滑动多少步可以到边缘。
c. 填充值zero-padding:在外围边缘补充若干圈0,方便从初始位置以步长为单位可以刚好滑倒末尾位置,通俗地讲就是为了总长能被步长整除。
下面这幅图片,是卷积操作的另一个示意图,与图2.2不同的是,我们这里的input是一个三维的输入,下图左侧的三个矩阵,分别代表了input X 在第三维度上的切片
根据我们之前的介绍,这个时候,我们的kernel也应该是三个维度,也就是下图中的 ω0
不过,这里我们用了两个kernel,分别是 ω0,ω1 ,对应的也就有了两个输出。
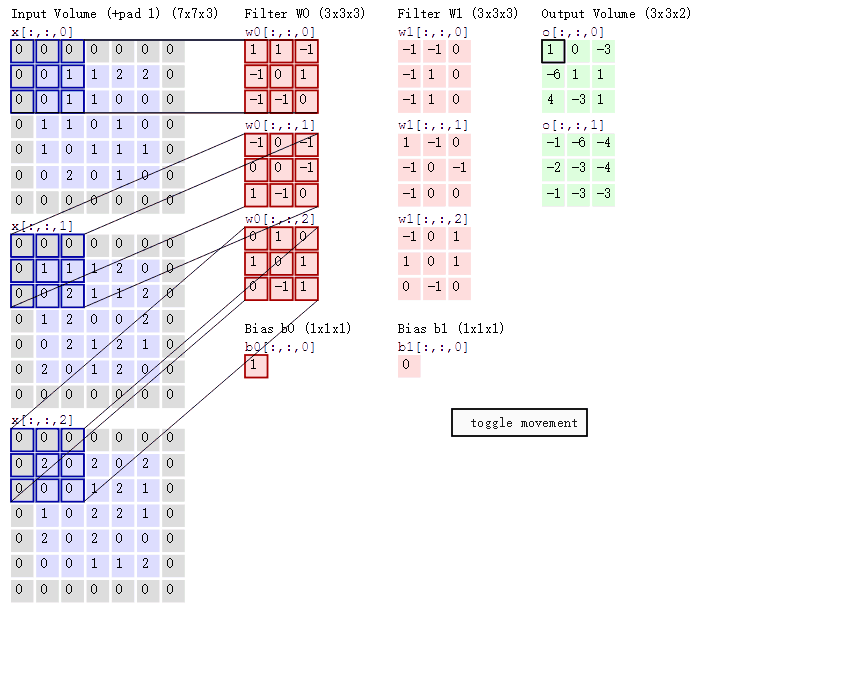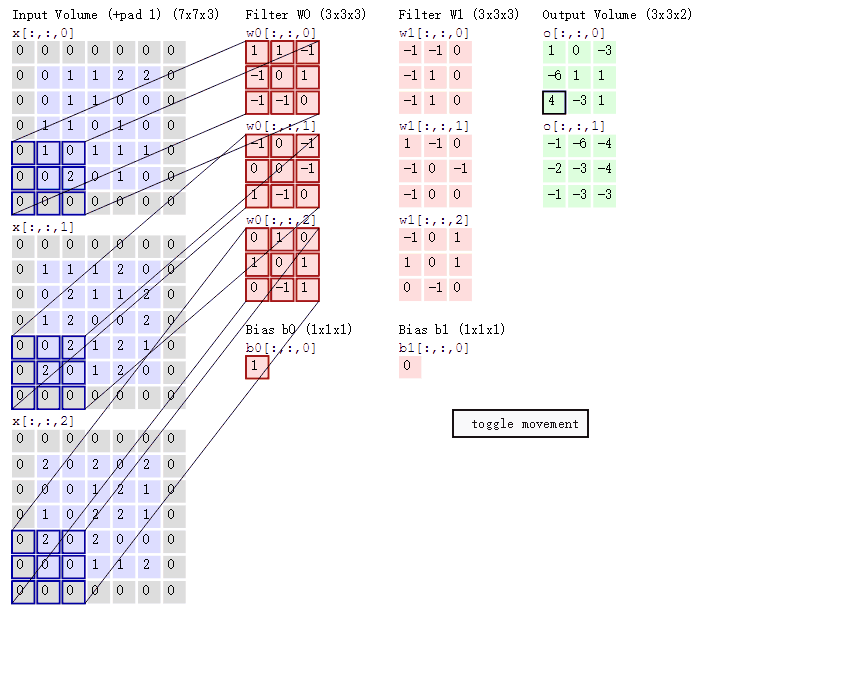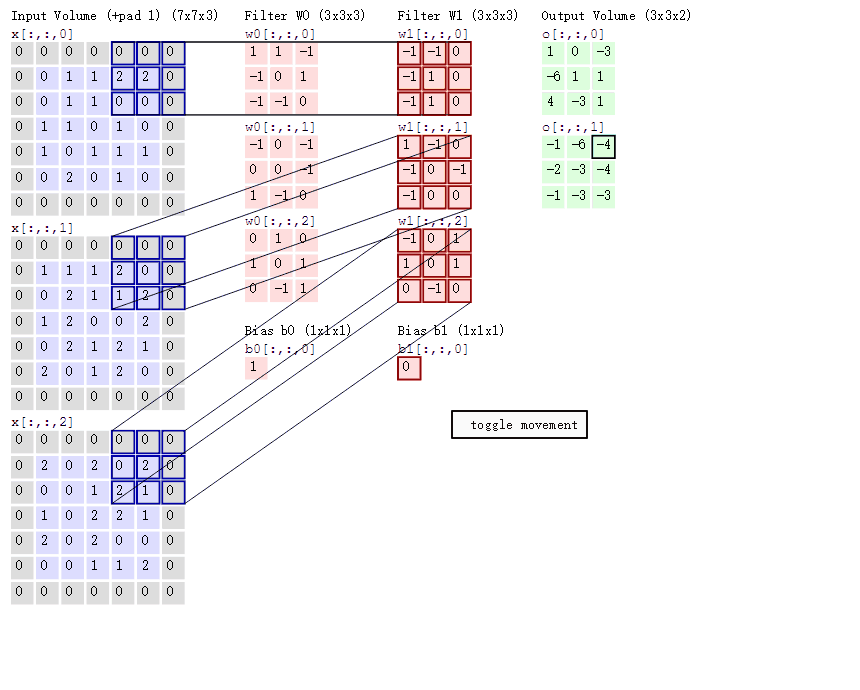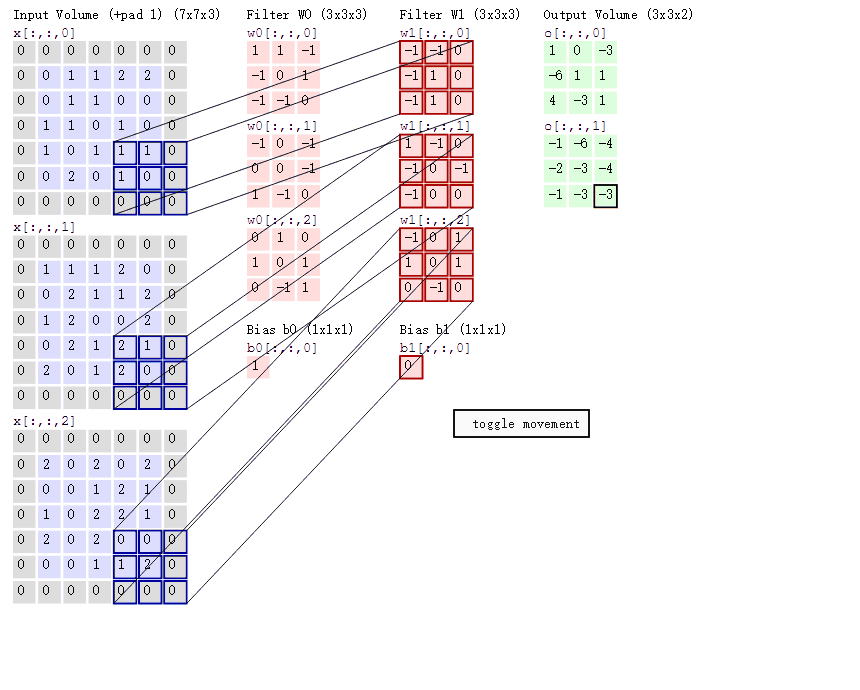
值得一提的是:
- 左边数据在变化,每次滤波器都是针对某一局部的数据窗口进行卷积,这就是所谓的CNN中的局部感知机制。
打个比方,滤波器就像一双眼睛,人类视角有限,一眼望去,只能看到这世界的局部。如果一眼就看到全世界,你会累死,而且一下子接受全世界所有信息,你大脑接收不过来。当然,即便是看局部,针对局部里的信息人类双眼也是有偏重、偏好的。比如看美女,对脸、胸、腿是重点关注,所以这3个输入的权重相对较大。 - 与此同时,数据窗口滑动,导致输入在变化,但中间滤波器Filter w0的权重(即每个神经元连接数据窗口的权重)是固定不变的,这个权重不变即所谓的CNN中的参数(权重)共享机制。
再打个比方,某人环游全世界,所看到的信息在变,但采集信息的双眼不变。btw,不同人的双眼 看同一个局部信息 所感受到的不同,即一千个读者有一千个哈姆雷特,所以不同的滤波器 就像不同的双眼,不同的人有着不同的反馈结果。
关于这个图片的具体计算过程,读者可以参考v_JULY_v的博文(点击此处)
进一步来说:

在左侧的网络中,我们用深黑线表示这些边的参数是相同的(事实上,在做卷积的时候,确实如此,这些边都是中间位置的边,对应的也是kernel的中间的值),可以看到在这个网络中,参数是共享的。而在右侧的矩阵乘积网络中,每一个边的参数,都不是共享的。
假如我们现在有
m
个输入和
我们有时候也把paremeter sharing叫做tied weights,因为应用在某一个输入的权重的值与其他位置上的权重值绑定在一起。在卷积网络中,kernel中的每一个元素都会作用在input的每个位置中(不考虑边界的话)。参数共享(parameter sharing)意味着,我们不需要对每一个位置都分别训练一套属于自己独有的参数。我们只需要一套参数就可以了。这不会改变前向传播的运行时间,事实上,它仍然是
O(k×n)
(见上一段).但是由于我们只需要存K个参数,因此降低了模型的存储要求。由于
k
比
3.3 equivariant representations
我们说一个函数具有等变性质(equivariant),意味着当输入改变时,输出也会以相同的方式改变。特别的,对于函数
f和g
,当
f(g(x))=g(f(x))
时,我们说函数
f(x)
对函数
g
等变。这个等式的含义很容易理解,对于函数

卷积函数就具有这样的性质。
例如,给定一个图像输入

即我们先对
当处理时间序列数据时,这意味着如果我们把输入中的一个事件向后延时,在输出中仍然会有完全相同的表示,只是时间延后了。图像与之类似,如果我们移动输入中的对象,它的表示也会在输出中移动同样的量。
当处理多个输入位置时,一些作用在邻居像素的函数是很有用的。 例如在处理图像时,在卷积网络的第一层进行图像的边缘检测是很有用的。 相同的边缘散落在图像的各处,所以应当对整个图像进行参数共享。 但在某些情况下,我们并不希望对整幅图进行参数共享。 例如,在处理已经通过剪裁而使其居中的人脸图像时,我们可能想要提取不同位置上的不同特征(处理人脸上部的部分网络需要去搜寻眉毛,处理人脸下部的部分网络就需要去搜寻下巴了)。
卷积对其他的一些变换并不是天然等变的,例如对于图像的放缩或者旋转变换,需要其他的一些机制来处理这些变换。
最后,对有些数据而言,用传统的矩阵乘法得到的神经网络可能不会做出很好的处理。这是我们可能通过卷积神经网络来处理,我们将会在接下来的博文中讲到。
4.小结
本篇博文主要讲了以下内容:
在理论部分,本博文首先介绍卷积的概念,然后我们解释在神经网络中使用卷积的原因:sparse interactions,parameter sharing和equivariant representations.
关于卷积更深入的理解,你可以参考这篇博文http://xiaosheng.me/2017/05/16/article60/
接下来的博文中,我们会介绍:
1. 池化
2. 一些在神经网络中常用的卷积函数
3. 如何在数据集上使用不同维度的卷积
4. 使得卷积操作更高效的方式
5. 使用tensorflow进行CNN的实现
6. 讨论如何使用CNN做中文文本分类。
请继续阅读:
《卷积神经网络CNN理论到实践(2)》
welcome!
sunxiangguodut@qq.com
http://blog.csdn.net/github_36326955

Welcome to my blog column: Dive into ML/DL!

I devote myself to dive into typical algorithms on machine learning and deep learning, especially the application in the area of computational personality.
My research interests include computational personality, user portrait, online social network, computational society, and ML/DL. In fact you can find the internal connection between these concepts:
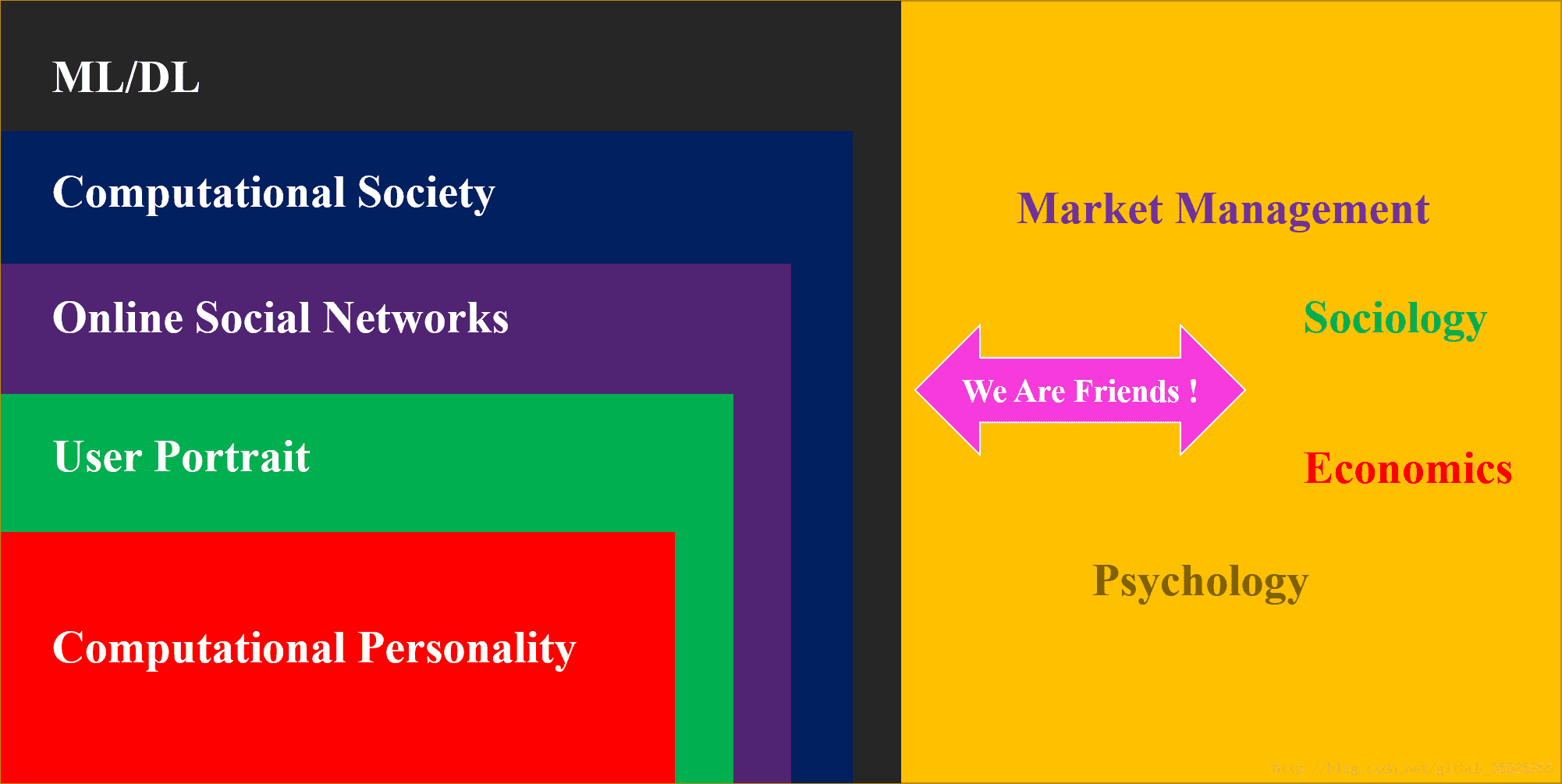
In this blog column, I will introduce some typical algorithms about machine learning and deep learning used in OSNs(Online Social Networks), which means we will include NLP, networks community, information diffusion,and individual recommendation system. Apparently, our ultimate target is to dive into user portrait , especially the issues on your personality analysis.
All essays are created by myself, and copyright will be reserved by me. You can use them for non-commercical intention and if you are so kind to donate me, you can scan the QR code below. All donation will be used to the library of charity for children in Lhasa.
手机扫一扫,即可:
























 9315
9315

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








