一、线性内插
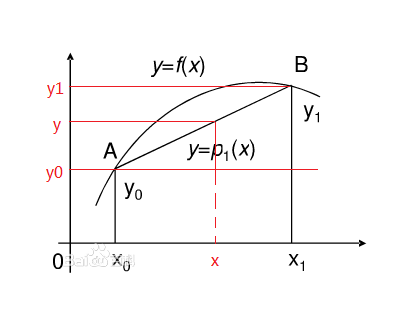
假设我们已知坐标(x0, y0)与(x1, y1),要得到[x0, x1]区间内某一位置在直线上的y值。
根据图中所示, 假设AB上有一点(x, y), 可作出两个相似三角形,我们得到 :
则:
这种y求解的方法叫做-----线性外插。 已知y求x的过程与以上过程相同,只是x与y要进行交换。
二、双线性插值
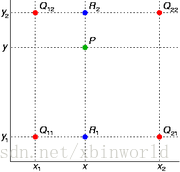
双线性插值,在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值,见下图
假如我们想得到未知函数 f 在点P = (x, y)的值,假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1)以及Q22 = (x2, y2)四个点的值。常见的情况,f 就是一个像素点的像素值。首先在x方向进行线性插值,得到
然后在y方向进行线性插值,得到
综合起来就是双线性插值最后的结果:
由于图像双线性插值只会用相邻的4个点,因此上述公式的分母都是1。 opencv中源码用了一些优化手段,比如用整数计算代替float,以及源图像和目标图像几何中心的对齐。








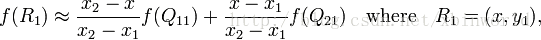
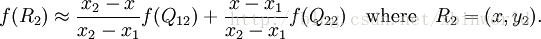
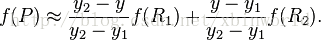
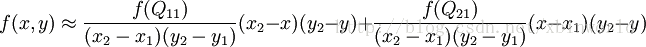
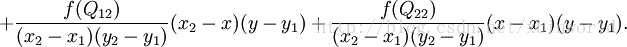
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








