一、单线性插值法
单线性插值法,也被称为一次插值法,是一种数学上的插值方法,其核心在于利用两个已知数据点之间的线性关系来估算这两个点之间的任意点的值。以下是关于单线性插值法的详细解释:
1.1、定义与原理
线性插值法假设在两个已知数据点(x₁, y₁)和(x₂, y₂)之间,任意点的值y可以通过线性关系进行估计。这意味着,我们假设在两个已知点之间,数据的变化是线性的,即可以用一条直线来近似表示这些点之间的数据关系。
1.2、算法步骤
- 确定已知数据点:
- 选择两个已知的数据点(x₁, y₁)和(x₂, y₂),其中x₁和x₂是已知的自变量值,y₁和y₂是对应的因变量值。
- 计算斜率:
- 使用公式m = (y₂ - y₁) / (x₂ - x₁)来计算这两个点之间的斜率。
- 估算未知数据点的值:
- 对于需要估算的任意点x,使用线性插值公式y = y₁ + m * (x - x₁)来计算对应的y值。
1.3、公式表示
单线性插值的公式可以表示为:
y = y₁ + ((y₂ - y₁) / (x₂ - x₁)) * (x - x₁)
其中,y是需要估算的未知数据点对应的值,x是未知数据点的自变量值,y₁和y₂是已知数据点的因变量值,x₁和x₂是已知数据点的自变量值。
1.4、推导过程

根据初中的知识,2点求一条直线公式(这是双线性插值所需要的唯一的基础公式)

经过简单整理成下面的格式:
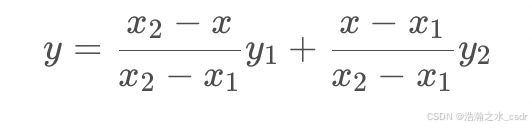
这里没有写成经典的AX+B的形式,因为这种形式从权重的角度更好理解。
首先看分子,分子可以看成x与x1和x2的距离作为权重,这也是很好理解的,P点与P1、P2点符合线性变化关系,所以P离P1近就更接近P1,反之则更接近P2。
现在再把公式中的分式看成一个整体,原式可以理解成y1与y2是加权系数,如何理解这个加权,要返回来思考一下,咱们先要明确一下根本的目的:咱们现在不是在求一个公式,而是在图像中根据2个点的像素值求未知点的像素值。这样一个公式是不满足咱们写代码的要求的。
现在根据实际的目的理解,就很好理解这个加权了,y1与y2分别代表原图像中的像素值(x与x1和x2的距离作为权重),上面的公式可以写成如下形式:
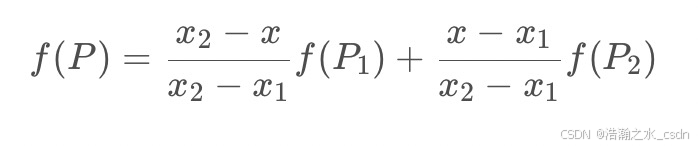
1.5、程序实现
单线性插值(也称为线性插值)是一种用于在两个已知数据点之间估计未知数据点的方法。其基本思想是通过连接两个已知点形成一条直线,然后在这条直线上找到所需的插值点。
下面是一个简单的Python实现,用于在两个已知点之间进行线性插值:
def linear_interpolation(x0, y0, x1, y1, x):
"""
在两个已知点 (x0, y0) 和 (x1, y1) 之间进行线性插值,以估计 x 处的 y 值。
参数:
x0, y0 -- 第一个已知点的坐标
x1, y1 -- 第二个已知点的坐标
x -- 需要估计的 x 值
返回:
y -- 估计的 y 值
"""
# 计算插值公式中的斜率
slope = (y1 - y0) / (x1 - x0)
# 使用插值公式计算 y 值
y = y0 + slope * (x - x0)
return y
# 示例使用
x0, y0 = 1, 2
x1, y1 = 3, 4
x = 2
y = linear_interpolation(x0, y0, x1, y1, x)
print(f"在 x = {x} 处的插值 y = {y}")在这个例子中,我们有两个已知点 (1, 2) 和 (3, 4),并希望估计 x = 2 处的 y 值。运行代码后,输出将是:
在 x = 2 处的插值 y = 3.0
这个实现是线性插值的基本形式,适用于在两个已知点之间进行插值。如果你需要在多个点之间进行插值,可以使用更高级的插值方法,如多项式插值或样条插值,或者使用NumPy库中的插值函数。
1.6、应用场景
单线性插值法在多个领域都有广泛的应用,包括但不限于:
- 数据平滑与填充:在信号处理、传感器数据处理等领域中,当某些数据缺失或需要平滑时,可以使用单线性插值来估算这些缺失或不平滑的数据点。
- 图像处理:在图像处理中,单线性插值常用于图像的缩放、旋转等操作。虽然它可能不如双线性插值或更高阶的插值方法精确,但由于其计算简单,因此在某些对图像质量要求不高的场合仍然得到应用。
- 物理模拟:在物理模拟中,单线性插值可以用于估算物体在连续时间内的位置、速度等物理量。
- 金融分析:在金融领域,单线性插值可以用于估算股票价格、汇率等金融指标在任意时刻的值。
1.7、优缺点
- 优点:
- 算法简单,易于实现。
- 计算速度快,适用于实时处理。
- 在数据变化较为线性时,插值效果较好。
- 缺点:
- 对于非线性数据,单线性插值可能会导致不准确的估算。
- 在存在大数据间隔或极端值的情况下,单线性插值可能会引入较大的误差。
综上所述,单线性插值法是一种简单实用的数学工具,在多个领域都有广泛的应用。然而,它也存在一定的局限性和缺陷,因此在使用时需要谨慎选择并结合具体情况进行分析。如果数据变化非线性较强,可以考虑使用更高阶的插值方法如双线性插值、二次插值或三次样条插值等。
二、双线性插值算法
双线性插值算法是一种在数学和计算机图形学中广泛使用的插值方法。其核心思想是在两个方向(通常是水平和垂直方向)上分别进行一次线性插值,从而得到未知点的估算值。以下是对双线性插值算法的详细解释:
2.1、定义与原理
双线性插值(Bilinear Interpolation)又称为一阶插值,是基于线性插值的一种扩展。它假设在一个二维平面上,四个已知点(通常是待插值点的左上、右上、左下和右下角)围成的区域内,数据的变化是线性的。因此,可以通过在这四个点之间进行两次线性插值(先水平后垂直,或先垂直后水平,结果相同)来估算待插值点的值。
2.2、算法步骤
- 定位待插值点:
- 确定待插值点的坐标(x, y)。
- 找到相邻的四个已知点:
- 根据待插值点的坐标,找到其周围的四个已知点,这四个点通常是待插值点在二维网格中的左上、右上、左下和右下角的四个点。
- 计算插值因子:
- 计算待插值点相对于这四个点的水平和垂直插值因子。水平插值因子通常表示为α,垂直插值因子通常表示为β。这些因子可以通过待插值点的坐标与相邻点的坐标之差来计算。
- 进行加权平均:
- 使用这四个已知点的值和计算出的插值因子,通过加权平均的方式计算出待插值点的值。加权平均的公式通常表示为:
f(x,y)=(1−α)(1−β)f(x0,y0)+α(1−β)f(x1,y0)+(1−α)βf(x0,y1)+αβf(x1,y1)
其中,f(x0, y0), f(x1, y0), f(x0, y1), 和 f(x1, y1) 分别是四个相邻点的值。
2.3、推导过程
假如我们想得到未知函数f在点P= (x,y) 的值,假设我们已知函数f在Q11 = (x1,y1)、Q12 = (x1,y2),Q21 = (x2,y1) 以及Q22 = (x2,y2) 四个点的值。

首先在x方向进行线性插值,得到R1和R2,
![]()
然后在y方向进行线性插值,得到P.
![]()
整合后的公式如下
![]()
2.4、程序实现
在图像处理的时候,我们先根据
srcX=dstX*(srcWidth/dstWidth)
srcY=dstY*(srcHeight/dstHeight)
来计算目标像素在源图像中的位置(和最近邻插值法一样,但是线性插值的像素是通过公式计算的),这里计算的srcX和srcY一般都是浮点数,
设坐标通过反向变换得到的浮点坐标为 (i+u,j+v) (其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素得值 f(i+u,j+v) 可由原图像中坐标所对应的周围四个像素的值决定,

计算公式由👆上面整合后的公式替换得到:
f(i+u,j+v) = (1-u)(1-v) f(i,j) + (1-u)v f(i,j+1) + u(1-v) f(i+1,j) + uv f(i+1,j+1)
注:
matlab、openCV对应的resize()函数的源坐标和目标坐标转换和一般的不一样。
是
SrcX=(dstX+0.5)* (srcWidth/dstWidth) -0.5
SrcY=(dstY+0.5) * (srcHeight/dstHeight)-0.5
# coding=utf-8
import cv2
import numpy as np
import time
def resize(src, new_size):
dst_w, dst_h = new_size # 目标图像宽高
src_h, src_w = src.shape[:2] # 源图像宽高
if src_h == dst_h and src_w == dst_w:
return src.copy()
scale_x = float(src_w) / dst_w # x缩放比例
scale_y = float(src_h) / dst_h # y缩放比例
# 遍历目标图像,插值
dst = np.zeros((dst_h, dst_w, 3), dtype=np.uint8)
for n in range(3): # 对channel循环
for dst_y in range(dst_h): # 对height循环
for dst_x in range(dst_w): # 对width循环
# 目标在源上的坐标(浮点值)
src_x = (dst_x + 0.5) * scale_x - 0.5
src_y = (dst_y + 0.5) * scale_y - 0.5
# 计算在源图上的(i,j),和(i+1,j+1)的值
src_x_0 = int(np.floor(src_x)) # floor是下取整
src_y_0 = int(np.floor(src_y))
src_x_1 = min(src_x_0 + 1, src_w - 1)
src_y_1 = min(src_y_0 + 1, src_h - 1)
# 双线性插值
value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, n] + (src_x - src_x_0) * src[src_y_0, src_x_1, n]
value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, n] + (src_x - src_x_0) * src[src_y_1, src_x_1, n]
dst[dst_y, dst_x, n] = int((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1)
return dst
if __name__ == '__main__':
img_in = cv2.imread('test.jpg')
start = time.time()
img_out = cv2.resize(img_in, (600,600))
print('cost %f seconds' % (time.time() - start))
cv2.imshow('src_image', img_in)
cv2.imshow('dst_image', img_out)
cv2.waitKey()
2.4、应用场景
双线性插值算法在多个领域都有广泛的应用,包括但不限于:
- 图像处理:
- 在图像缩放、旋转、裁剪等操作中,双线性插值常用于估算新像素的值,以保持图像的平滑性和细节。
- 计算机图形学:
- 在三维图形渲染中,双线性插值可用于纹理映射,即根据纹理坐标在纹理图像中查找并估算对应像素的颜色值。
- 信号处理:
- 在数字信号处理中,双线性插值可用于信号的重采样和滤波等操作。
- 数据可视化:
- 在数据可视化领域,双线性插值可用于生成平滑的二维数据图表和图像。
2.5、优缺点
- 优点:
- 算法相对简单,易于实现。
- 在大多数情况下,能够提供较为平滑的插值结果。
- 计算效率较高,适用于实时处理。
- 缺点:
- 在数据变化非线性较强时,插值结果可能不够准确。
- 可能会引入一定的模糊效应,特别是在边缘和纹理复杂的区域。
- 相比更高阶的插值方法(如双三次插值),双线性插值在保留细节方面可能稍显不足。
综上所述,双线性插值算法是一种在多个领域都有广泛应用的插值方法。它以其简单性、高效性和平滑性而著称,但在处理非线性数据和保留细节方面存在一定的局限性。因此,在选择插值方法时,需要根据具体的应用场景和数据特性进行权衡。
参考:


























 1050
1050

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










