数据结构-线段树

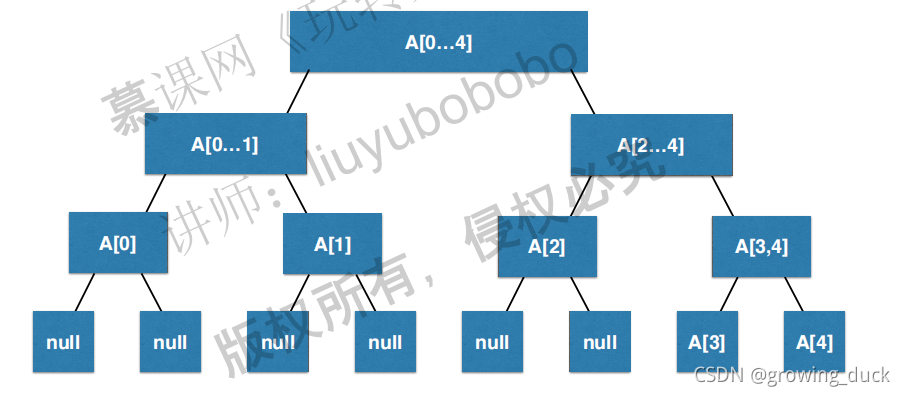
 如上图：

线段树是一颗满二叉树，叶子节点如果没有值，用null表示。 非空叶子节点就是基础数据，树中每个父亲节点代表左右孩子的结果集（比如求合，最大值，最小值等，自己定义算法，传入左右孩子即可）。

那么有n个元素，构建线段树需要开辟多少空间？

对于满二叉树，每一层节点数量都是前面所有节点数量之和+1。 也就是说，如果最后一层有n个节点，整棵树就约为2n个节点。

如果此时n为2的k次方，所有元素刚好在最后一层，整棵树约就是2n。   如果再多一个元素，就需要开辟下一层空间，如上图那样，整棵树就需要开辟4n的空间。

构建线段树：

使用两个数组来构建线段树，一个数组表示原始数据，另一个数组表示线段树。

如上图所示，如果传入一个数组，如何把它构建为线段树？ 

public class SegmentTree<E> {
    //存储数据
    private E[] data;
    //用数组表示树结构
    private E[] tree;
    //定义算法类，计算左右孩子的结果。 此例中为求合
    private Merger<E> merger;

    //外界传入一个数组arr，将它构建为线段树（每个树节点就是左右