在看青蛙台阶的算法时想法到一个问题
f(n)=f(n-1)+f(n-2)
青蛙在n-1阶,有f(n-1)种跳法。
在n-2阶,有f(n-2)种跳法。
那么n-1到n有一种跳法,就是跳一阶。
n-2到n有一种跳法,跳两阶。
那为什么最后到n阶的跳法不是
f(n)=f(n-1)+f(n-2)+2呢?
让我们先从0阶开始往5阶跳的顺序。
 再让我们看从5阶往0阶跳的逆序
再让我们看从5阶往0阶跳的逆序
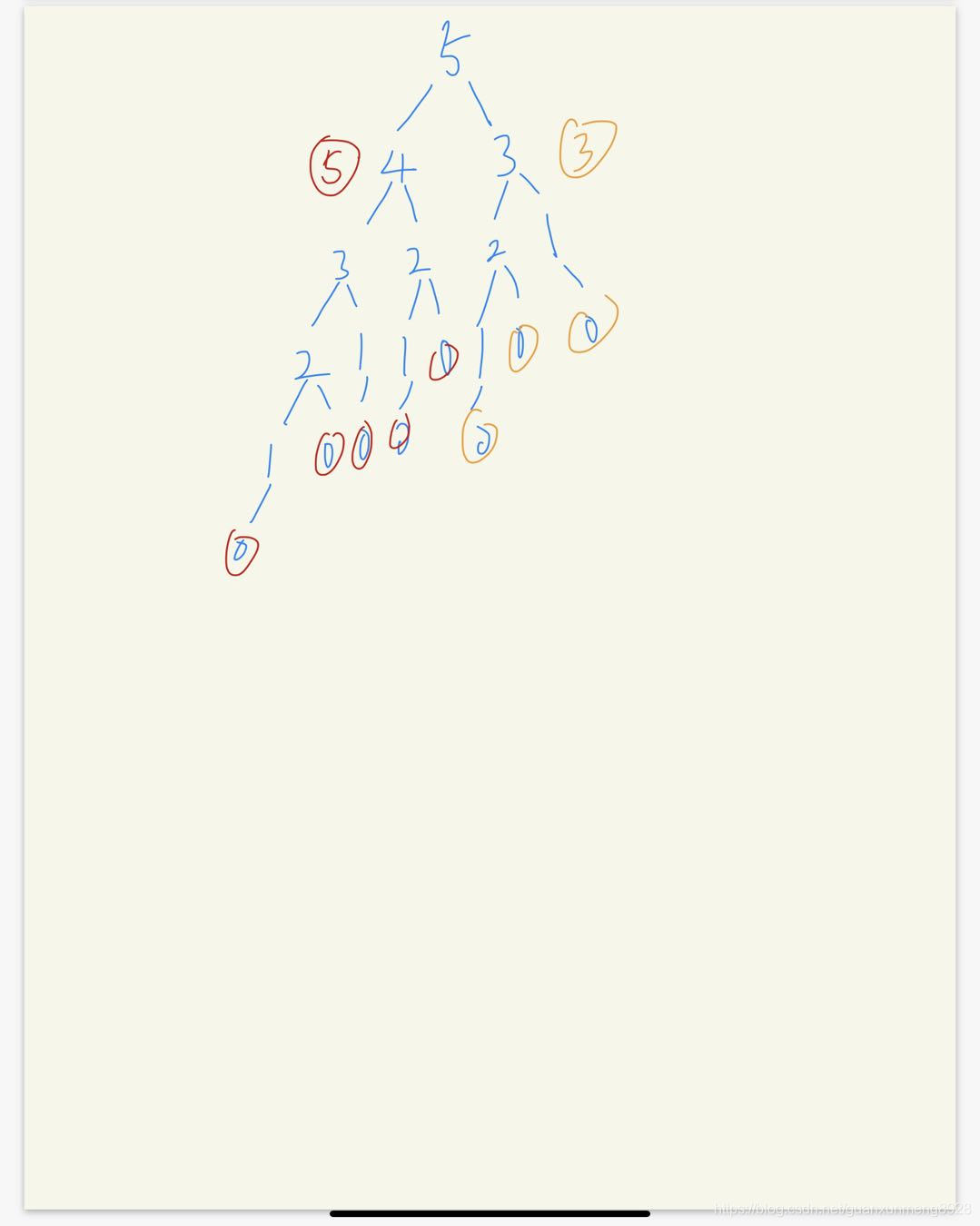 通过逆序我们可以看到,想要到达5阶,青蛙就必须先要到达4阶和3阶,那么0阶到4阶或者0阶到3阶的路线总数已经确定,也就意味着起点数目已经确定(也就是0的个数)。 那么到5阶,只需要统计4阶和3阶的起点数,就可以知道,到5阶有多少种路线。
通过逆序我们可以看到,想要到达5阶,青蛙就必须先要到达4阶和3阶,那么0阶到4阶或者0阶到3阶的路线总数已经确定,也就意味着起点数目已经确定(也就是0的个数)。 那么到5阶,只需要统计4阶和3阶的起点数,就可以知道,到5阶有多少种路线。
因为最后从n-1阶跳到n阶只有一种跳法不会增加跳法。
也就是说:1阶跳到n-1再跳到n阶的跳法总数 == 1阶跳到n-1阶的跳法总数
同理:1阶跳到n-2再跳到n阶的跳法总数 == 1阶跳到n-2阶的跳法总数
那么这个规律也就符合斐波那契公式。
//计算跳台阶的方法
int calcWays(int &number){
if(number<0) return false;
if(number<1) return 0;
if(number==1) return 1;
if(number==2) return 2;
step=0; a=1; b=2;
for(int i=3;i<number+1;i++)
{
step=a+b;
a=b;
b=a;
}
return step;
}





















 4008
4008











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








