ResNet_残差网络

打开深度之门——残差网络

产生残差网络的原因：虽然网络越越复杂能够完成的任务越多。深效果越好。但达到一定层数后，accuracy就会下降，这种问题称为degradation，该问题不同于梯度消失/梯度爆炸。梯度消失/梯度爆炸从一开始就阻碍网络收敛，我们通过标准初始化或者中间层归一化已经能够解决。
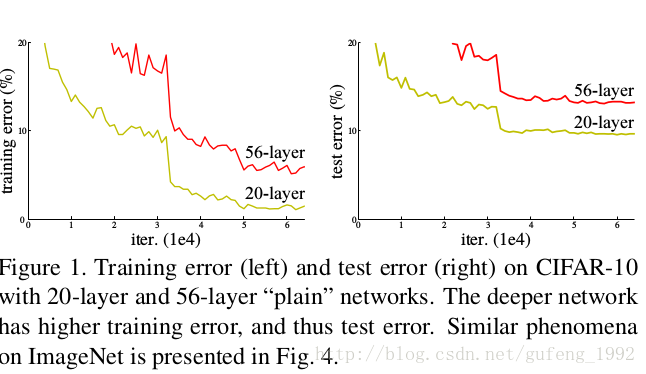
当深度增加时，准确率达到饱和然后迅速下降，并且这种误差和过拟合无关，在增加层数时也使训练错误率下降厉害，如下图所示。

解决方案：残差学习
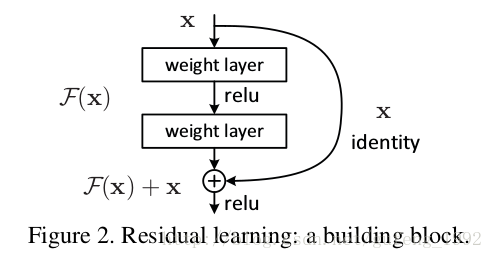
残差，顾名思义，肯定带有差值，是谁的差值，输入和输出的，而且是几层（2/3）模块的输入和输出的差值，如图所示

我们这样考虑：这两层网络只是拟合到一个未定的映射（underlying mapping），我们定义为H(x), 我们考虑不让模块拟合到H(x)，而是然它拟合到原输出H(x)和输入的差x，即：f(x) = H(x)-x.则原输出就为f(x)+x。作者只是假设拟合残差f(x)要比拟合H(x)容易，事实证明是正确的。而且，极端情况下，在一个恒等映射下，如果它是最优的，那么将残差推到零比通过一堆非线性层拟合一个恒等映射更容易。进而我们如果将恒等映射连接到网络下面错误率将不会大于对应原网络。这样我们就能够增加网络层数而错误率也不会降低。
残差的可以用跳跃连接实现，如上图所示，从输入有一条直接连接到输出的连接，没有任何参数（输出，输入维度相同）。就能实现残差的连接。
那它是如何提高正确率呢？
degradation问题表示，网络所能表达的方程很难接近于恒等表示（这样错误率不大于对应浅层网络）。我们假设如果最终结果要求是恒等映射那么相当于我们使用残差网络拟合到0
映射。这是可以实现的。
在现实例子中，恒等映射不可能使深层网络最优，但我们重新构造有可能解决这个问题。如果一个最优函数是更接近一个恒等映射而不是0映射，对一个求解器来说，找到恒等映射的扰动比重新学习一个函数更简单。

使用跳跃连接来实现恒等映射

如上图所示，我们定义的这个模块公式如下：

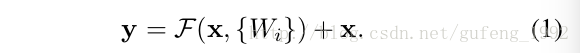
x和y分别是输入和输出。
表示学习到的残差函数。

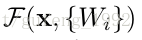
上面公式成立前提条件是f(x)和x维度必须一致，如果维度不一致就需要一个线性转化来实现维度一致

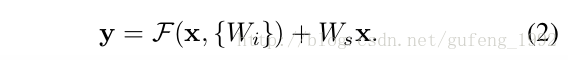
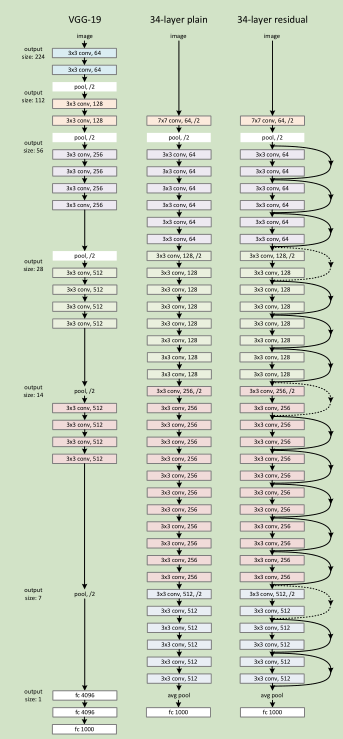
网络结构：