一个小推广:
- 我搬运的分子生物物理学课程,感觉讲得特别好,老师是分子动力学领域的大牛
- 院士讲座:分子动力学与药物发现
- 更多搬运课程请关注我的B站主页
概述
-
MD是一种计算机模拟分子运动的方法。原子受到其他粒子的力,从而发生运动。通常这运动只是在平衡态附近的振动。
-
构象空间:一定范围内,改变键参数(键角、二面角等),产生的所有可能的构象。每个构象对应一个势能,连起来就是势能面。势能面上有许多局部最优点,可能对应某个稳定的构象。
基本原理
经典力学
MD应用牛顿力学:
m
d
2
r
i
d
t
2
=
F
i
=
−
∇
V
(
r
i
)
m\dfrac{\mathrm{d}^2\boldsymbol{r_i}}{\mathrm{d}t^2}=\boldsymbol{F_i}=-\nabla \boldsymbol{V}(\boldsymbol{r_i})
mdt2d2ri=Fi=−∇V(ri)
r
i
\boldsymbol{r_i}
ri是原子
i
i
i的位置,
F
i
\boldsymbol{F_i}
Fi是其受的力,
V
(
r
i
)
\boldsymbol{V}(\boldsymbol{r_i})
V(ri)是该处的势能。势能和每个原子的位置、类型(质量)、电荷等信息都有关。有了加速度,就可以更新每个原子的速度,进而更新位置,再返回来更新加速度。
由此我们得到各原子的状态(构象)随时间的变化曲线(trajectory),以此来分析动态变化过程,或者求统计平均值计算某种性质。
在牛顿力学下,体系一般遵循能量守恒定律。势能降低,动能就要升高。总能量和设定的环境(温度等)密切相关,对模拟影响很大。势能零点一般取平衡态。
势能的组成(重点)
不同力场有不同组成,仅此介绍几个基本元素。一般可分成两类:
V
=
V
b
o
n
d
e
d
+
V
n
o
n
−
b
o
n
d
e
d
V=V_{bonded}+V_{non-bonded}\\
V=Vbonded+Vnon−bonded
非键势能
V n o n − b o n d e d = V v d w + V e l e V_{non-bonded}=V_{vdw}+V_{ele} Vnon−bonded=Vvdw+Vele
范德华力
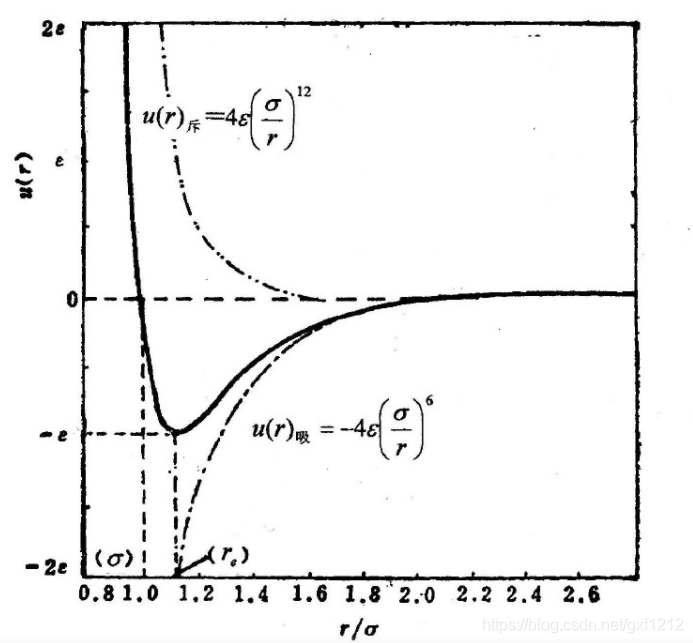
这里的范德华力指两个原子间的,由原子间斥力(核与核、电子和电子)和吸引力(核与电子)组成,两项分别为:
V
v
d
w
=
∑
n
o
n
−
b
o
n
d
e
d
a
t
o
m
p
a
i
r
s
4
ε
i
j
(
(
σ
i
j
r
i
j
)
12
−
(
σ
i
j
r
i
j
)
6
)
V_{vdw}=\sum_{non-bonded\\atom\ pairs} 4\varepsilon_{ij}\left((\dfrac{\sigma_{ij}}{{r_{ij}}})^{12}-(\dfrac{\sigma_{ij}}{{r_{ij}}})^{6}\right)
Vvdw=non−bondedatom pairs∑4εij((rijσij)12−(rijσij)6)
或
V
v
d
w
=
∑
n
o
n
−
b
o
n
d
e
d
a
t
o
m
p
a
i
r
s
ε
i
j
(
(
r
e
r
i
j
)
12
−
2
(
r
e
r
i
j
)
6
)
V_{vdw}=\sum_{non-bonded\\atom\ pairs} \varepsilon_{ij}\left((\dfrac{r_e}{r_{ij}})^{12}-2(\dfrac{r_e}{{r_{ij}}})^{6}\right)
Vvdw=non−bondedatom pairs∑εij((rijre)12−2(rijre)6)
这里是MD中常用的Lennard-Jones函数。其中
- r i j r_{ij} rij是原子间距离
- ε i j \varepsilon_{ij} εij是势能最低点到势能零点(无限远处)的能量差
- r e r_e re是势能最低点处的间距, σ i j \sigma_{ij} σij指势能零点处的间距
点击查看完整推导
特点:
- 每两个原子间其实都有,所以计算很耗时
- 和原子类型相关,从实验数据得来
静电力
表达式由库伦定律而来:
V
e
l
e
=
∑
n
o
n
−
b
o
n
d
e
d
a
t
o
m
p
a
i
r
s
q
i
q
j
ε
D
r
i
j
V_{ele}=\sum_{non-bonded\\atom\ pairs}\dfrac{q_iq_j}{\varepsilon_D r_{ij}}
Vele=non−bondedatom pairs∑εDrijqiqj
-
静电力是从原子整体角度看的,并不把核与电子分开。 q q q指的是,因为电负性差异导致分子内电荷分布不均,原子带上的形式电荷。
比如一个羰基,C的电子云被O吸走,C原子处等效存在一定量正电荷。
所以,同性为正,异性为负。
-
ε D \varepsilon_D εD指环境的相对介电常数。因为模拟不是在真空而是水溶液进行,所以 ε D > 1 \varepsilon_D>1 εD>1。溶液浓度越高,值越大。
键势能
V b o n d e d = V b o n d + V a n g l e + V d i h e d r a l V_{bonded}=V_{bond}+V_{angle}+V_{dihedral} Vbonded=Vbond+Vangle+Vdihedral
成键原子间、化学键之间存在相互作用,处在平衡位置时是能量最低、最稳定的。偏离了平衡位置,势能就会升高。
键长势能

键长势能和电子重叠程度有关,为使能量降低,不能太近或太远。把化学键简化成简谐振子,其势能为
V
b
o
n
d
=
1
2
∑
b
o
n
d
s
K
b
(
b
−
b
0
)
2
V_{bond}=\dfrac{1}{2}\sum_{bonds}K_b(b-b_0)^2
Vbond=21bonds∑Kb(b−b0)2
- K b K_b Kb是键常数。值越大,则键越难被拉伸。
- b b b是成键原子间距离, b 0 b_0 b0是理想键长(最稳定的原子间距离)。
- 也可添加高次非简谐项。
键角势能

两个键(偶极矩)间的排斥和吸引力。键角势能和轨道形状有关,越偏离则势能越大。
V
a
n
g
l
e
=
1
2
∑
a
n
g
l
e
s
K
θ
(
θ
−
θ
0
)
2
V_{angle}=\dfrac{1}{2}\sum_{angles}K_\theta(\theta-\theta_0)^2
Vangle=21angles∑Kθ(θ−θ0)2
参数意义类似。
二面角势能

如图,当2-3单键旋转(固定1-2或3-4),1,2,3所在平面和2,3,4所在平面所成的角度,或是沿2-3看去,1-2键和3-4键的投影所成的角度变化。2、3连接的几个基团间有可能因位阻而排斥,角度的变化导致位阻变化,势能变化。
V
b
o
n
d
=
1
2
∑
d
i
h
e
d
r
a
l
s
K
ϕ
(
1
+
cos
(
n
ϕ
−
δ
)
)
V_{bond}=\dfrac{1}{2}\sum_{dihedrals}K_\phi(1+\cos(n\phi-\delta))
Vbond=21dihedrals∑Kϕ(1+cos(nϕ−δ))
- n n n是整数,取决于两端基团的对称性。一般没有对称性时应取 n = 1 n=1 n=1,2或3连接 k k k个相同原子或基团时, n = k n=k n=k。
- ϕ \phi ϕ的取值范围是 − π ∼ π -\pi\sim\pi −π∼π, cos \cos cos函数保证 ϕ \phi ϕ增加 2 π 2\pi 2π时势能值不变。
- δ \delta δ是相角,用来调节最小势能对应的角度。
- K ϕ K_\phi Kϕ指能量最高点和最低点势能之差。
- 该式适用于KaTeX parse error: Undefined control sequence: \ce at position 1: \̲c̲e̲{-CH2-CH2 -}型二面角,即其他基团都相同,势能曲线才有余弦对称性。如果基团变复杂,可以添加高次的余弦函数。
总结
-
几种力
-
这五种作用可能涵盖了主要的作用力种类。静电力外的其他作用其实本质上也都是电磁力。
- 非键势能主要描述相距远的原子,直接用原子间相互作用力描述。
- 键势能主要描述相距较近的原子,用偏离平衡态的程度来描述。
-
三种键势能中的作用力分别需要相连的两个、三个、四个原子来组成。
-
所有这些能量都是对真实作用力的近似和模型化,可能会与真实情况有差异。
-
-
力场
力场指的是势能表达式和参数的组合。选择一个力场,就是同时选择势能的形式和参数。
-
参数
- 参数指的是,上面公式中除了 r i j r_{ij} rij外的所有变量。
- 参数的来源包括
- QM(量子力学)计算
- 实验测定和统计
求解算法
基本算法
因为不能求得解析解,就用数值解法。取一个
Δ
t
\Delta t
Δt(通常是
1
f
s
=
1
×
1
0
−
15
s
1\mathrm{fs}=1\times 10^{-15}\mathrm{s}
1fs=1×10−15s 左右),更新速度:
v
(
t
+
Δ
t
)
=
v
(
t
)
+
a
(
t
)
Δ
t
\boldsymbol{v}(t+\Delta t)=\boldsymbol{v}(t)+\boldsymbol{a}(t)\Delta t
v(t+Δt)=v(t)+a(t)Δt
然后更新位置:
r
(
t
+
Δ
t
)
=
r
(
t
)
+
v
(
t
)
Δ
t
\boldsymbol{r}(t+\Delta t)=\boldsymbol{r}(t)+\boldsymbol{v}(t)\Delta t
r(t+Δt)=r(t)+v(t)Δt
Verlet算法
准确来说,应该对牛顿第二定律积分。根据上述更新速度的公式:
v
(
T
)
=
v
(
t
)
+
a
(
t
)
(
T
−
t
)
\boldsymbol{v}(T)=\boldsymbol{v}(t)+\boldsymbol{a}(t)(T-t)
v(T)=v(t)+a(t)(T−t)
从
T
=
t
T=t
T=t到
t
+
Δ
t
t+\Delta t
t+Δt积分得:
r
(
t
+
Δ
t
)
=
r
(
t
)
+
v
(
t
)
Δ
t
+
1
2
a
(
t
)
(
Δ
t
)
2
\boldsymbol{r}(t+\Delta t)=\boldsymbol{r}(t)+\boldsymbol{v}(t)\Delta t+\dfrac{1}{2}\boldsymbol{a}(t)(\Delta t)^2
r(t+Δt)=r(t)+v(t)Δt+21a(t)(Δt)2
但事实上,我们还没考虑加加速度、加加加速度(继续求导)等,所以准确的表达式应该是做泰勒展开:
r
(
t
+
Δ
t
)
=
∑
i
=
0
∞
1
i
!
r
(
i
)
(
t
)
(
Δ
t
)
i
\boldsymbol{r}(t+\Delta t)=\sum_{i=0}^\infty \dfrac{1}{i!}\boldsymbol{r}^{(i)}(t)(\Delta t)^i
r(t+Δt)=i=0∑∞i!1r(i)(t)(Δt)i
我们取前三项:
r
(
t
+
Δ
t
)
=
r
(
t
)
+
v
(
t
)
Δ
t
+
1
2
a
(
t
)
(
Δ
t
)
2
+
1
6
j
(
t
)
(
Δ
t
)
3
+
o
(
Δ
t
4
)
\boldsymbol{r}(t+\Delta t)=\boldsymbol{r}(t)+\boldsymbol{v}(t)\Delta t+\dfrac{1}{2}\boldsymbol{a}(t)(\Delta t)^2+\dfrac{1}{6}\boldsymbol{j}(t)(\Delta t)^3+o(\Delta t^4)
r(t+Δt)=r(t)+v(t)Δt+21a(t)(Δt)2+61j(t)(Δt)3+o(Δt4)
从
T
=
t
T=t
T=t到
t
−
Δ
t
t-\Delta t
t−Δt积分得:
r
(
t
−
Δ
t
)
=
r
(
t
)
−
v
(
t
)
Δ
t
+
1
2
a
(
t
)
(
Δ
t
)
2
−
1
6
j
(
t
)
(
Δ
t
)
3
+
o
(
Δ
t
4
)
\boldsymbol{r}(t-\Delta t)=\boldsymbol{r}(t)-\boldsymbol{v}(t)\Delta t+\dfrac{1}{2}\boldsymbol{a}(t)(\Delta t)^2-\dfrac{1}{6}\boldsymbol{j}(t)(\Delta t)^3+o(\Delta t^4)
r(t−Δt)=r(t)−v(t)Δt+21a(t)(Δt)2−61j(t)(Δt)3+o(Δt4)
两者相加、移项得到:
r
(
t
+
Δ
t
)
=
2
r
(
t
)
−
r
(
t
−
Δ
t
)
+
a
(
t
)
(
Δ
t
)
2
+
o
(
Δ
t
4
)
\boldsymbol{r}(t+\Delta t)=2\boldsymbol{r}(t)-\boldsymbol{r}(t-\Delta t)+\boldsymbol{a}(t)(\Delta t)^2+o(\Delta t^4)
r(t+Δt)=2r(t)−r(t−Δt)+a(t)(Δt)2+o(Δt4)
o
(
Δ
t
4
)
o(\Delta t^4)
o(Δt4)可忽略,只是表示误差的数量级。这样就可以通过前两步的位移来计算下一步位移。
速度则用下式计算:
v
(
t
)
=
r
(
t
+
Δ
t
)
−
r
(
t
−
Δ
t
)
2
Δ
t
+
o
(
Δ
t
2
)
\boldsymbol{v}(t)=\dfrac{\boldsymbol{r}(t+\Delta t)-\boldsymbol{r}(t-\Delta t)}{2\Delta t}+o(\Delta t^2)
v(t)=2Δtr(t+Δt)−r(t−Δt)+o(Δt2)
-
优点
-
简单,比基本算法更精确
-
对内存要求不高
-
只要位置时,可以不用算速度
-
时间可逆性:也可以倒过来算 r ( t − Δ t ) \boldsymbol{r}(t-\Delta t) r(t−Δt)
摘自维基百科:A deterministic process is time-reversible if the time-reversed process satisfies the same dynamic equations as the original process; in other words, the equations are invariant or symmetrical under a change in the sign of time. A stochastic process is reversible if the statistical properties of the process are the same as the statistical properties for time-reversed data from the same process.
-
较高(数值)稳定性,也遵循能量守恒
-
-
缺点
- 不能自启动:第一步还是得先算速度
- 因为 Δ t \Delta t Δt很小,所以速度中的 1 Δ t \dfrac{1}{\Delta t} Δt1可能造成较大误差。速度的误差数量级和位置不同。
为什么要算速度?
反应中会改变温度,就是通过改变速度来影响原子的运动的。
蛙跳(Leap-Frog)算法
已知初始位置和
1
2
Δ
t
\dfrac{1}{2}\Delta t
21Δt前的速度,则可得到下一个
Δ
t
\Delta t
Δt的速度::
v
(
t
+
1
2
Δ
t
)
=
v
(
t
−
1
2
Δ
t
)
+
a
Δ
t
\boldsymbol{v}(t+\dfrac{1}{2}\Delta t)=\boldsymbol{v}(t-\dfrac{1}{2}\Delta t)+\boldsymbol{a}\Delta t
v(t+21Δt)=v(t−21Δt)+aΔt
然后得到下一个
Δ
t
\Delta t
Δt的位置:
r
(
t
+
Δ
t
)
=
r
(
t
)
+
v
(
t
+
1
2
Δ
t
)
Δ
t
\boldsymbol{r}(t+\Delta t)=\boldsymbol{r}(t)+\boldsymbol{v}(t+\dfrac{1}{2}\Delta t)\Delta t
r(t+Δt)=r(t)+v(t+21Δt)Δt
也就可以估算速度:
v
(
t
)
=
(
v
(
t
+
1
2
Δ
t
)
+
v
(
t
−
1
2
Δ
t
)
)
/
2
\boldsymbol{v}(t)=\left(\boldsymbol{v}(t+\dfrac{1}{2}\Delta t)+\boldsymbol{v}(t-\dfrac{1}{2}\Delta t)\right)/2
v(t)=(v(t+21Δt)+v(t−21Δt))/2
它保留了Verlet算法的优势,又更准确地估计速度,只是计算量稍大一点点。
MD模拟实际方法
特点
- 原子会一直在势能最低点附近振动,而不是收敛
- 一段时间后,速率就会服从Boltzmann分布
- 一般是能量守恒,但由于数值误差(四舍五入),长时间模拟可能使总能量缓慢升高,需要加入一定机制来“保持”恒温。
溶剂
真实体系不能在真空中。
| 模型 | 显式溶剂模型 | 隐式溶剂模型 |
|---|---|---|
| 含义 | 模拟时加入水分子 | 用拟合模型表示水的作用 |
| 计算量 | 较大 | 较小 |
| 准确度 | 较高 | 较低 |
边界条件
通常不会选取一个有真实边界的体系(如一滴溶液),不仅可能使体系过大,而且模拟算法会使边界效应加重。
于是采用周期性边界条件,即选取一个小重复单元(孤立体系),比如稀溶液中一个分子、材料的一小段重复排列。
如采用一个立方体,为保持体系粒子数不变,当某个粒子从某个面离开,它将从对面同样位置出现,继续运动。这就如同,假设周围各方向都是该单元的重复排列,和中心单元同步运动,当蓝色粒子从右边离开时,左边盒子的蓝色粒子又进入这个盒子。但我们只研究中心盒子中的粒子。

截断法
同时,我们不考虑离得太远的原子对体系的作用,以减少计算量。我们会设置一个截断距离作为考虑作用力的边界,使得误差在可接受的范围内。它通常是一个球面。截断面必须完全处于盒子之内,也就是说盒子要足够大。
在截断面之外,势能函数可以简化为:
- 直接设为0;
- 或者一个容易计算的、越远越趋近于0的近似函数。
软件、力场和应用
- 常见软件:AMBER, NAMD, GROMACS, Desmond, OpenMM, CHARMM
- 可视化软件:VMD and PyMOL(不止用在MD)
- 生物分子常用力场:AMBER, CHARMM, OPLS-AA
加速计算的方法
非键势能是原子间两两作用,所以计算量和原子数的平方成正比。最耗时的就是非键势能
-
减少步数,即增大 Δ t \Delta t Δt
-
改进、简化算法,减少每步的时间
- 截断法,只考虑有限的范围
- 较多地忽略范德华力,因为它随距离变长下降很快
- 冻结特定的、并不显著变化的运动,如快速振动
- 粗粒化模型,以更大的原子团为单位
-
减少模拟时间
- 并不模拟真实需要的时间,而是类似于“倍速”模拟,如原本需2微秒的过程只用1微秒完成
- 人工添加外力,把反应物拉近、产物拉开等
只在特定条件下用
-
并行计算
- 用GPU(核数多,很有效)
- 控制多个处理器各自负责一个区域
-
改进硬件性能
- 使用超算
模拟过程
-
确定初始结构
- 数据库或同源建模
- 找到原子坐标信息
-
检查overlap,防止初始结构不合理
-
设定拓扑结构和力场
- topology:原子类型、连接,电荷
- 力场:势函数、参数
-
能量最小化
- 方法:最速下降、共轭梯度、quasi-newton、Newton-Raphson等
- 防止模拟时能量太高直接爆炸
-
加溶剂、离子等
这些条件对构象影响很大
-
选定温度、压强等
通常选恒温恒压(NPT),即生理温度(37℃)、一个标准大气压
-
模拟设置
关于如何运行程序(分段之类的)、保存数据等
-
平衡
从低温逐渐升至设定的温度。如研究蛋白和配体的结合,就先让两者稳定接触,达到平衡态。
-
主模拟
记录能量等随时间的变化,得到trajectory
-
数据分析
用软件或编程分析结果,计算性质

*MD特点和局限性总结
为什么用MD?
- 实验上的解析不能涵盖所有细节。计算机模拟可细致研究
- 分子的构象空间、平衡态性质
- 分子的动态性质(随时间变化)、统计性质(“平均”结构)等
- 分子的互作机制
- 还可以根据已知的结构预测未知结构分子的功能
MD的局限性
-
时间尺度
生物体系中,某些运动所需时间 τ \tau τ很短,为了保证精度,必须满足 τ Δ t ≈ 20 \dfrac{\tau}{\Delta t}\approx 20 Δtτ≈20,这使模拟时间延长。但有时整个生物过程又特别长。
时间是MD模拟的一个瓶颈,一次简单的模拟就可耗费一周时间。
-
力场精度
虽然一直在优化,但势函数毕竟是近似的,参数也是引入的。
也没有一种既普适又精确的力场,需要根据经验选择(或自己做实验)。
-
不能描述反应
化学键是设定好的,不能断。也就不能描述二硫键形成、质子转移等常见过程。
解决:相应部分用QM计算
和QM对比
| 特点 | MD/力场法 | ab initio QM |
|---|---|---|
| 原理 | 分子力学(经典力学) | 量子力学 |
| 基本研究对象 | 原子(原子团) | 所有电子及分布 |
| 研究体系大小 | 大 | 小 |
| 计算相同体系需要的时间 | 短 | 长 |
| 计算准确度 | 相对低,但也足够研究 | 很精确 |
| 计算得到的性质 | 部分性质 | 所有物理性质 |
| 能否描述化学反应 | 不能(要加反应力场) | 能 |
| 是否包含随时间的变化 | 是 | 有些可以 |
| 是否引入参数/半经验 | 是 | 否 |
所以力场法可看作为解决大体系而对QM方法的一种简化。
MD的尺度


MD的应用
- Membrane proteins: Environment, Dynamics & Interactions
- Ligand-receptor binding
- Protein Folding
- Mechanism of enzyme catalyst
- Structural refinement (resolved by NMR, X-ray, Cryo-EM)
- Free energy calculation
在结构解析中,常和核磁配合,解析动态结构
拓展阅读
- 翻译的讲义
- 本文主要根据我校老师课件的思路整理而来,并引用了几张图片



























 587
587

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










