0.做题的时候很害怕遇到这类问题,尤其是和斯托克斯定理高斯散度定理格林定理混在一起的时候。估计是,在学校学的时候,这块应该也是没有理解的,只是把各种定理的形式记住,然后做题的时候生搬硬套。这些天似乎是明白了一点,所以写下来,完全是自己的理解,有不对的地方请指正。
多元积分分类,简单到复杂:
累次积分
二重积分,三重积分
曲线积分(第一型,第二型),曲面积分(第一型,第二型)
1. 曲线的切线 , 曲面的法线
| 用参数方程表示 | 用曲面方程表示 | |
| 曲线方程 | x=X(t) y=Y(t) z=Z(t) | P(x,y,z)=0 Q(x,y,z)=0 |
| 曲面方程 | x=X(u,v) y=Y(u,v) z=Z(u,v) | F(x,y,z)=0 |
相应的切线和法线表示
| 用参数方程表示 | 用曲面方程表示 | |
| 曲线的切线 | ( X', Y', Z' ) | (P' x,P' y,P' z) X (Q' x,Q' y,Q' z) |
| 曲面的法线 | (X' u,Y' u,Z' u)X (X' v,Y' v,Z' v) | (F' x,F' y,F' z) |
2. 曲线积分和曲面积分的微元
| 带方向微元 | 用参数方程表示 | 用曲面方程表示 |
| 曲线积分微元dL | ( X', Y', Z' )dt | - |
| 曲面积分微元dS | (X' u,Y' u,Z' u)X (X' v,Y' v,Z' v)dudv | - |
注:a.微元方向必然与切线或法线方向一致,上两个表格的黄色部分一致
b.由于微元可以在参数方程的情况下表示出来,所以可以用来计算;否则只能通过第二类积分转换为关于坐标的微分(dx,dy,dz,dydz,dzdx,dxdy),才能进行计算。
3. 第一类积分和第二类积分的转换
a.曲线积分
方向补充说明:
如果 t 增加的方向和曲线方向 (L 的方向)是相反,那么从第三步开始增加负号,到最后的一步变为有负号的结果。这时按 t 增加的方向定义起点和终点,和按照 L 的方向定义的起点终点是相反的,如果把最后一步的积分起点终点颠倒,则可以吸收负号,结果恰为按照L的方向的积分。
推导过程中dt 的上下限,为从小到大,即从小到大积分(不这样应该也可以)
b.曲面积分
和上面的推导类似
方向补充说明:
关于方向性:
a.坐标积分的方向性
第一类曲线或曲面积分是没有方向的,也就是说只要被积函数是正的,那么积分值也是正的。
但是当第一类积分代入参数方程,并且曲线微元或者面积微元换为参数微元(即上面的dl变为dt)后,积分变得有方向性。即使被积函数是正的,当积分的上下限不同时,可能会造成积分值为负的情况。
对于曲线积分,要求参数是从小积到打
对于曲面积分,两个参数都从小到大?
b.第二类积分的方向
对曲线积分,从推导过程可以看出,
4. 关于叉乘,矩阵的行列式,面积,坐标转换
a.叉乘可以用矩阵的行列式以方便计算
b.坐标转换的矩阵的行列式,对应微元的面积或者体积比
c.由于叉乘之于三维空间的特殊性,所以以上结论可能被限制在三维空间中
5. 斯托克斯公式,格林公式,保守场
对于函数 F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z),如果可以找到另一个函数f(x,y,z),使得f(x,y,z)的梯度等于F,则说F的保守的。(单连通区域)
这时,
保守场的性质可以看做斯托克斯公式的特殊情形。
格林公式也可以以看成斯托克斯公式在R=0,P=P(x,y),Q=Q(x,y) 时的情况。
wiki说微积分基本定理和高斯定理是广义的斯托克斯定理的推广,大概涉及到微分几何的内容,这个地方我没有想清楚。
关于几个定理,wiki上的这个表总结的比较全:
http://zh.wikipedia.org/wiki/%E5%90%91%E9%87%8F%E5%BE%AE%E7%A9%8D%E5%88%86
| 定理 | 表示 | 注解 |
|---|---|---|
| 梯度定理 (线积分基本定理) | C为一平滑曲线。 | |
| 格林定理 | 在封闭曲线C上所做的线积分, 等于在区域D所的积分。 | |
| 高斯散度定理 (散度基本定理) | ||
| 斯托克斯定理 (旋度基本定理) |
6.电磁学的高斯定理和高斯散度公式
一直感觉有关系,但是好像关系不大,或者不是想象中的那样。q/ε这个东东是用曲面积分就算出来的。电场的强度在产生该场的电荷处是没有定义的,所以散度公式是不能直接用的。但是把电场强度代入散度公式,被积函数变为0,也就是说在不包括点电荷的区域中,电场的通量为0。









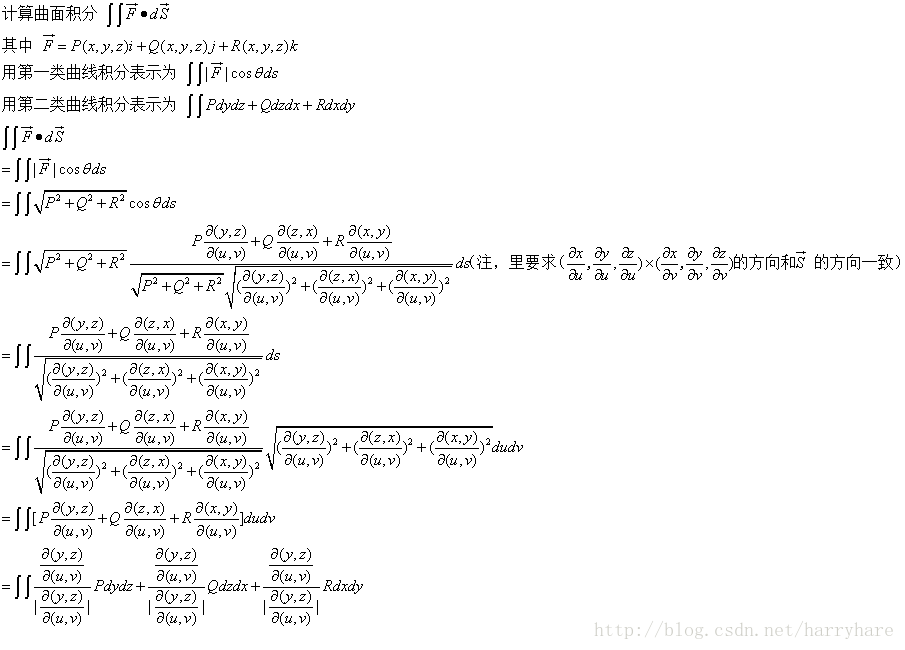


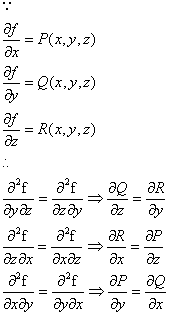

















 313
313

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








