Median of Two Sorted Arrays 两个有序数组的中位数@LeetCode

超级难的一道题，线性时间复杂度好做，就是merge。

但是对数复杂度，就要用到很多数学分析，实际上就是要找到第k小的元素。

翻遍了网络，觉得还是这一篇讲的最详细，而且写得代码最容易转为Java，因为Java无法像C++一样把数组名作为指针，进而操作。

http://nriverwang.blogspot.com/2013/04/k-th-smallest-element-of-two-sorted.html

http://www.youtube.com/watch?v=_H50Ir-Tves  这个算法应该对应的是最后一个讲解的算法。

这里复制一下分析过程：

K-th Smallest Element of Two Sorted Arrays

K-th Smallest Element of Two Sorted Arrays

Problem Description:

---

Given two sorted arrays A and B of size m and n, respectively. Find the k-th (1 <= k <= m+n) smallest element of the total (m+n) elements in O(log(m)+log(n)) time.

Analysis:

---

This is a popular interview question and one special case of this problem is finding the median of two sorted arrays. One simple solution is using two indices pointing to the head of A and B, respectively. Then increase the index pointing to the smaller element by one till  k elements have been traversed. The last traversed element is the k-th smallest one. It is simple but the time complexity is  O(m+n).

To get  O(log(m)+log(n)) time complexity, we may take advantage of binary search because both of the two arrays are sorted. I first read the binary search method from this  MIT handout, which aims to find the median of two sorted arrays. This method can be easily modified to solve the  k-th smallest problem:

First of all, we assume that the  k-th smallest element is in array A and ignore some corner cases for basic idea explanation. Element  A[i] is greater than or equal to  i elements and less than or equal to all the remaining elements in array A ( A[i] >= A[0..i-1] && A[i] <= A[i+1..m-1]). If A[i] is the  k-th smallest element of the total ( m + n)  elements ( A[i] >= k-1 elements in A+B and  <= all other elements in A+B), it must be greater than or equal to  (k - 1 - i)elements in B and less than or equal to all the remaining elements in B ( A[i] >= B[k - 1 - i - 1]  && A[i] <= B[k - 1 - i]). Below figure shows that  A[i] (in gray) is greater than or equal to all green elements ( k-1 in all) in A+B and less than or equal to all blue elements in A+B.

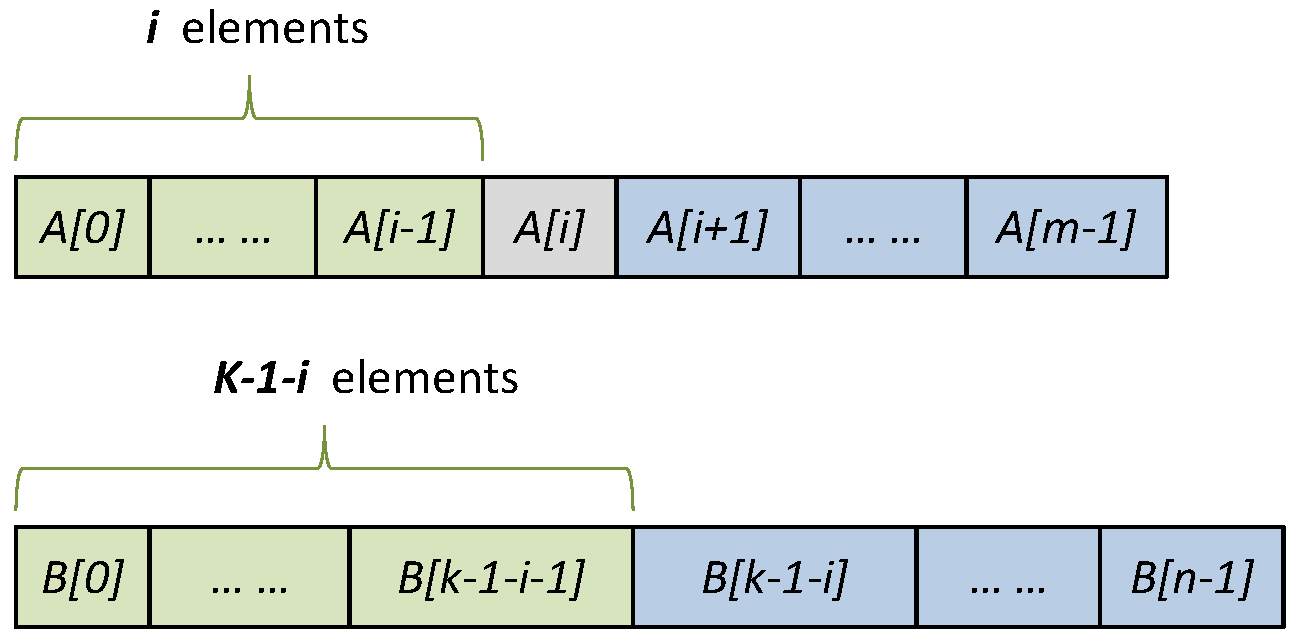
Then it becomes very easy for us to check whether A[i] >= B[k - 1 - i - 1]  and A[i] <= B[k - 1 - i]. If so, just returnA[i] as the result; if not, there are two cases:

1).  A[i] > B[k - 1 - i], which means  A[i] is greater than more than  k elements in both A and B. The  k-thsmallest element must be in the lower part of A ( A[0..i-1]); 

2). otherwise, the  k-th smallest element must be in the higher part of A ( A[i+1..m-1]).

The search begins with range  A[0..m-1]  and every time  i  is chosen as the middle of the range, therefore we can reduce the search size by half until we find the result.

The above algorithm looks good, but it won't give you correct answer because there are many corner cases need to be addressed:

1). The simplest one may be that the  k-th smallest element is in B rather than in A. When the entire array A has been traversed and no answer is returned, it means the   k-th smallest element must be in B (if  k is valid, i.e.  1 <= k <= m+n). We just need to run another "binary search" in B and this time the correct answer is guaranteed to be returned. 

2).  i >= k. This means  A[i] is greater than or equal to  k elements in A and will be at least the  ( k+1)- thelement in A+B. In this case, we need to "binary search" in the lower part of A. 

3).  i + n < k - 1. Similarly to case 2), this means  A[i] will be at most the  (k-1)-th element in A+B. In this case, we need to "binary search" in the higher part of A. 

4). At any time when we refer  B[k - 1 - i - 1] and  B[k - 1 - i], we should assure the indices are in range [0, n) to avoid out of array bounds error.

The binary search on A and B takes  O(log(m))  and  O(log(n))  time respectively, so the worst case time complexity is  O(log(m)+log(n)) . For the problem of finding median of two sorted arrays, the  ((m+n)/2 + 1)-th  element should be returned if  (m+n)  is odd. If  (m+n)  is even, the average of the  ((m+n)/2)-th  and  ((m+n)/2 + 1)-th  elements is returned. Below is the code in c++.

/**
 * Search the k-th element of A[0..m-1] and B[0..n-1] in A[p..q]
 */
int kth_elem(int A[], int m, int B[], int n, int k, int p, int q) {
    if (p > q)
        return kth_elem(B, n, A, m, k, 0, n-1);//search in B
        
    int i = p + (q - p) / 2;
    int j = k - 1 - i - 1;
        
    if ((j < 0 || (j < n && A[i] >= B[j])) 
        && (j+1 >= n || (j+1 >= 0 && A[i] <= B[j+1]))) {
        return A[i];
    } else if (j < 0 || (j+1 < n && A[i] > B[j+1])) {
        return kth_elem(A, m, B, n, k, p, i-1);
    } else {
        return kth_elem(A, m, B, n, k, i+1, q);
    }   
}

double median_two_arrays(int A[], int m, int B[], int n) {
    if ((m + n) % 2 == 1) {
        return kth_elem(A, m, B, n, (m+n)/2+1, 0, m-1);
    } else {
        return (kth_elem(A, m, B, n, (m+n)/2, 0, m-1) +
                kth_elem(A, m, B, n, (m+n)/2+1, 0, m-1)) / 2.0;
    }
}

package Level5;

import java.util.Arrays;


/**
 * 
 * Median of Two Sorted Arrays 
 * 
 * There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)). 
 *
 */
public class S4 {

	public static void main(String[] args) {
		int A[] = {};
		int B[] = {2,3};
		System.out.println(findMedianSortedArrays(A, B));
	}

	// O(m+n) merged
	public static double findMedianSortedArrays2(int A[], int B[]) {
		int lena = A.length;
		int lenb = B.length;
		int[] merged = new int[lena+lenb];
		int i= 0, j = 0, k = 0;
		while(i<lena || j<lenb){
			if(j==lenb || (i<lena && A[i]<B[j])){
				merged[k++] = A[i++];
			}else if(i==lena || (j<lenb && A[i]>=B[j])){
				merged[k++] = B[j++];
			}
		}
		
		int lenc = merged.length;
		if(lenc%2 != 0){
			return merged[lenc/2];
		}else{
			return (merged[lenc/2]+merged[lenc/2-1])/2.0;
		}
	}
	
	/**
	 * Search the k-th element of A[0..m-1] and B[0..n-1] in A[low..high]
	 */
	public static int kth_elem(int A[], int B[], int k, int low, int high) {
		int m = A.length;
		int n = B.length;
	    if (low > high)
	        return kth_elem(B, A, k, 0, n-1);	//search in B
	        
	    int i = low + (high - low) / 2;
	    int j = k - 1 - i - 1;
	    
	    // 找到第k小的元素
	    if ((j < 0 || (j < n && A[i] >= B[j])) && (j+1 >= n || (j+1 >= 0 && A[i] <= B[j+1]))) {
	        return A[i];
	    } else if (j < 0 || (j+1 < n && A[i] > B[j+1])) {		// 在A的左半边
	        return kth_elem(A, B, k, low, i-1);
	    } else {			// 在A的右半边
	        return kth_elem(A, B, k, i+1, high);
	    }   
	}

	public static double findMedianSortedArrays(int A[], int B[]) {
		int m = A.length;
		int n = B.length;
	    if ((m + n) % 2 == 1) {
	        return kth_elem(A, B, (m+n)/2+1, 0, m-1);
	    } else {
	        return (kth_elem(A, B, (m+n)/2, 0, m-1) +
	                	kth_elem(A, B, (m+n)/2+1, 0, m-1)) / 2.0;
	    }
	}
}

Analysis

We can solve this problem with the algorithm: Finding the Kth element in two sorted arrays. It’s quite straight forward. For example, supposing the total length of two arrays is N. If N is an odd number, we need to find the (N + 1) / 2 th number in two arrays, otherwise we need to find N / 2 th and (N + 1) / 2 th number and return the average of them.

The question requires a solution of O(log(m + n)) complexity. So we cannot do a linear search in these two arrays. But we can use a solution which is very similar to binary search.

For example, assuming we have the following two sorted arrays.

0	1	2	3	4	5
a0	a1	a2	a3	a4	a5

0	1	2	3	4	5
b0	b1	b2	b3	b4	b5

In this solution, we use mid = length / 2 to calculate the mid point position. The mid element of array A is A[3], and the mid element of array B is B[3]. We can divide each of them into two parts:

A_1(A[0], A[1], A[2]), A_2(A[3], A[4], A[5])

B_1(B[0], B[1], B[2]), B_2(B[3], B[4], B[5]).

Now we can compare A[3] with B[3]. If A[3] <= B[3], we know that the second part of B is equal or larger than any elements in the first part of A and B. We want the K th element in these two arrays. We have two situation here.

1. If K is smaller than the length of A_1 and B_1, we know that this element should not be in B_2. So we can throw this part and continue searching K th element in A and B_1.
2. If K is larger than the length of A_1 and B_1, K th element is not in A_1. Otherwise K will be smaller than the sum of length of A_1 and B_1. And then we can continue searching K – A_1.length th element in A_2 and B.

It’s quite similar for the situation A[3] > B[3]. The code is as follow.

public class Solution {
    public double findMedianSortedArrays(int A[], int B[]) {
        int lengthA = A.length;
        int lengthB = B.length;
        if ((lengthA + lengthB) % 2 == 0) {
            double r1 = (double) findMedianSortedArrays(A, 0, lengthA, B, 0, lengthB, (lengthA + lengthB) / 2);
            double r2 = (double) findMedianSortedArrays(A, 0, lengthA, B, 0, lengthB, (lengthA + lengthB) / 2 + 1);
            return (r1 + r2) / 2;
        } else
            return findMedianSortedArrays(A, 0, lengthA, B, 0, lengthB, (lengthA + lengthB + 1) / 2);
    }
 
    public int findMedianSortedArrays(int A[], int startA, int endA, int B[], int startB, int endB, int k) {
        int n = endA - startA;
        int m = endB - startB;
 
        if (n <= 0)
            return B[startB + k - 1];
        if (m <= 0)
            return A[startA + k - 1];
        if (k == 1)
            return A[startA] < B[startB] ? A[startA] : B[startB];
 
        int midA = (startA + endA) / 2;
        int midB = (startB + endB) / 2;
 
        if (A[midA] <= B[midB]) {
            if (n / 2 + m / 2 + 1 >= k)
                return findMedianSortedArrays(A, startA, endA, B, startB, midB, k);
            else
                return findMedianSortedArrays(A, midA + 1, endA, B, startB, endB, k - n / 2 - 1);
        } else {
            if (n / 2 + m / 2 + 1 >= k)
                return findMedianSortedArrays(A, startA, midA, B, startB, endB, k);
            else
                return findMedianSortedArrays(A, startA, endA, B, midB + 1, endB, k - m / 2 - 1);
 
        }
    }
}

If the length of an array is smaller or equal than zero, we know that we can directly get the K th element from the other array.

And If K = 1, we can just compare the first element and decide which one is the answer.

One thing needs to mention is that the comparison of k and the length of A_1 and B_1. We not only throws the half part of an array, we also throws the mid element out. So we will compare k with n / 2 + m + 2 + 1. And we throws half of the element like k – n / 2 – 1 or k – m / 2 – 1, in which “1” denoting the mid element. We are doing this because it can make sure that every time we will throw at least one element, otherwise sometimes it is possible that the solution is not able to stop.

Complexity

The complexity of this algorithm is O(log (m + n)).

http://www.lifeincode.net/programming/leetcode-median-of-two-sorted-arrays-java/