机器学习中常见的损失函数
一般来说,我们在进行机器学习任务时,使用的每一个算法都有一个目标函数,算法便是对这个目标函数进行优化,特别是在分类或者回归任务中,便是使用损失函数(Loss Function)作为其目标函数,又称为代价函数(Cost Function)。
损失函数是用来评价模型的预测值
Ŷ =f(X)
Y
^
=
f
(
X
)
与真实值
Y
Y
的不一致程度,它是一个非负实值函数。通常使用来表示,损失函数越小,模型的性能就越好。
设总有
N
N
个样本的样本集为,
yi,i∈[1,N]
y
i
,
i
∈
[
1
,
N
]
为样本
i
i
的真实值,为样本
i
i
的预测值,为分类或者回归函数。
那么总的损失函数为:
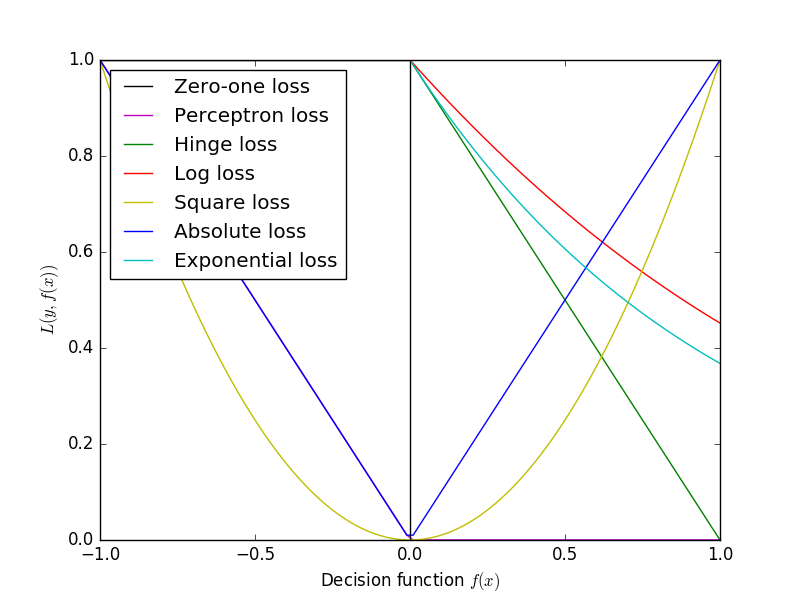
常见的损失函数 ℓ(yi,yi^) ℓ ( y i , y i ^ ) 有以下几种:
Zero-one Loss
Zero-one Loss即0-1损失,它是一种较为简单的损失函数,如果预测值与目标值不相等,那么为1,否则为0,即:
可以看出上述的定义太过严格,如果真实值为1,预测值为0.999,那么预测应该正确,但是上述定义显然是判定为预测错误,那么可以进行改进为Perceptron Loss。
Perceptron Loss
Perceptron Loss即为感知损失。即:
其中 t t 是一个超参数阈值,如在PLA(Perceptron Learning Algorithm,感知机算法)中取。
Hinge Loss
Hinge损失可以用来解决间隔最大化问题,如在SVM中解决几何间隔最大化问题,其定义如下:
更多请参见: Hinge-loss。
Log Loss
在使用似然函数最大化时,其形式是进行连乘,但是为了便于处理,一般会套上log,这样便可以将连乘转化为求和,由于log函数是单调递增函数,因此不会改变优化结果。因此log类型的损失函数也是一种常见的损失函数,如在LR(Logistic Regression, 逻辑回归)中使用交叉熵(Cross Entropy)作为其损失函数。即:
规定
Square Loss
Square Loss即平方误差,常用于回归中。即:
Absolute Loss
Absolute Loss即绝对值误差,常用于回归中。即:
Exponential Loss
Exponential Loss为指数误差,常用于boosting算法中,如AdaBoost。即:
正则
一般来说,对分类或者回归模型进行评估时,需要使得模型在训练数据上使得损失函数值最小,即使得经验风险函数最小化,但是如果只考虑经验风险(Empirical risk),容易过拟合(详细参见防止过拟合的一些方法),因此还需要考虑模型的泛化能力,一般常用的方法便是在目标函数中加上正则项,由损失项(Loss term)加上正则项(Regularization term)构成结构风险(Structural risk),那么损失函数变为:
其中 λ λ 是正则项超参数,常用的正则方法包括:L1正则与L2正则,详细介绍参见: 防止过拟合的一些方法。
























 3090
3090

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








