1. (10 分) 把 6 个不同的球放入 5 个不同的盒子,不允许空盒,有多少种放法?
答:
C(6,2) * 5 !=15 * 120=1800 , 共有 1800 种放法。
2. (10 分) 现在有 4 对夫妻围着圆桌就座,至少有一对夫妻不相邻的坐法有多少种?
答: (2021 国考真题)
4 对夫妻围着圆桌就座的坐法有 (4 * 2-1) !=7 ! 种
每对夫妻都相邻的坐法有: (4-1)!*2^4=96 种
则至少有一对夫妻不相邻的坐法有 7 !-96=4944 种
3. (10 分) 20 个顶点的三部图,最多能有多少条边?
答:
三部图, 即包含三个内部各顶点不相邻但与其它两部分都相邻的图。下图为一个 6 个顶点的三部图的例子。
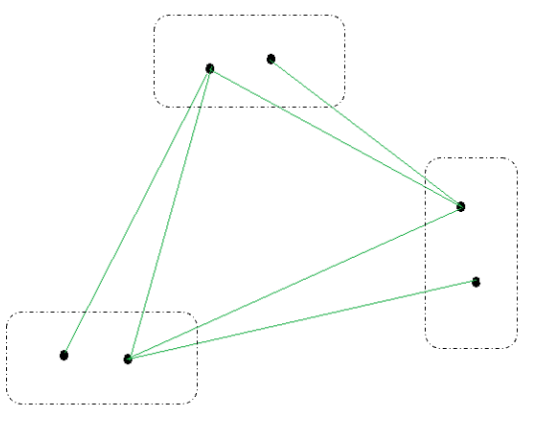
当三部图的三个部分平均分配顶点时,三部图的边数最多。所以 20 个顶点的三部图,每个部分平分顶点,分别有 7 、 7 、 6 个顶点,此时三部图有 ( 7 ∗ 13 + 7 ∗ 13 + 6 ∗ 14 ) / 2 = 133 \left(7^{*} 13+7^{*} 13+6 * 14\right) / 2=133 (7∗13+7∗13+6∗14)/2=133 条边。
4. (10 分) 设数列 { a n } \left\{a_{n}\right\} {an} 和 { b n } \left\{b_{n}\right\} {bn} 的母函数分别是 A ( x ) \mathrm{A}(x) A(x) 和 B ( x ) \mathrm{B}(x) B(x) 。如果 b n = ∑ i = 0 n ( a i ) \boldsymbol{b}_{\boldsymbol{n}}= \sum_{i=0}^{n}\left(a_{i}\right) bn=∑i=0n(ai) , 且 B ( x ) = f ( x ) A ( x ) \mathrm{B}(x)=f(x) A(x) B(x)=f(x)A(x) , 求 f ( x ) f(x) f(x) 。
答: (2019 国考真题)
设数列
{
a
i
}
\left\{a_{i}\right\}
{ai}的母函数为
A
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
\mathrm{A}(x) = a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + \cdots
A(x)=a0+a1x+a2x2+a3x3+⋯,
数列
{
b
i
}
\left\{b_{i}\right\}
{bi}的母函数为
B
(
x
)
=
b
0
+
b
1
x
+
b
2
x
2
+
b
3
x
3
+
⋯
\mathrm{B}(x) = b_{0} + b_{1}x + b_{2}x^{2} + b_{3}x^{3} + \cdots
B(x)=b0+b1x+b2x2+b3x3+⋯。
已知
b
k
=
a
0
+
a
1
+
a
2
+
a
3
+
⋯
+
a
k
b_{k} = a_{0} + a_{1} + a_{2} + a_{3} + \cdots + a_{k}
bk=a0+a1+a2+a3+⋯+ak,
因此,
B
(
x
)
\mathrm{B}(x)
B(x)可以表示为:
B
(
x
)
=
a
0
+
(
a
0
+
a
1
)
x
+
(
a
0
+
a
1
+
a
2
)
x
2
+
(
a
0
+
a
1
+
a
2
+
a
3
)
x
3
+
⋯
\mathrm{B}(x) = a_{0} + (a_{0} + a_{1})x + (a_{0} + a_{1} + a_{2})x^{2} + (a_{0} + a_{1} + a_{2} + a_{3})x^{3} + \cdots
B(x)=a0+(a0+a1)x+(a0+a1+a2)x2+(a0+a1+a2+a3)x3+⋯
接下来,我们计算
B
(
x
)
−
A
(
x
)
\mathrm{B}(x) - \mathrm{A}(x)
B(x)−A(x):
B
(
x
)
−
A
(
x
)
=
a
0
x
+
(
a
0
+
a
1
)
x
2
+
(
a
0
+
a
1
+
a
2
)
x
3
+
⋯
=
x
(
a
0
+
a
1
x
+
a
2
x
2
+
a
3
x
3
+
⋯
)
=
x
⋅
B
(
x
)
\begin{aligned} \mathrm{B}(x) - \mathrm{A}(x) &= a_{0}x + (a_{0} + a_{1})x^{2} + (a_{0} + a_{1} + a_{2})x^{3} + \cdots \\ &= x(a_{0} + a_{1}x + a_{2}x^{2} + a_{3}x^{3} + \cdots) \\ &= x \cdot \mathrm{B}(x) \end{aligned}
B(x)−A(x)=a0x+(a0+a1)x2+(a0+a1+a2)x3+⋯=x(a0+a1x+a2x2+a3x3+⋯)=x⋅B(x)
由此可得:
B
(
x
)
=
A
(
x
)
+
x
⋅
B
(
x
)
\mathrm{B}(x) = \mathrm{A}(x) + x \cdot \mathrm{B}(x)
B(x)=A(x)+x⋅B(x)
⇒
B
(
x
)
−
x
⋅
B
(
x
)
=
A
(
x
)
\Rightarrow \mathrm{B}(x) - x \cdot \mathrm{B}(x) = \mathrm{A}(x)
⇒B(x)−x⋅B(x)=A(x)
⇒
A
(
x
)
=
(
1
−
x
)
⋅
B
(
x
)
\Rightarrow \mathrm{A}(x) = (1 - x) \cdot \mathrm{B}(x)
⇒A(x)=(1−x)⋅B(x)
因此, f ( x ) = B ( x ) A ( x ) = 1 1 − x f(x) = \frac{\mathrm{B}(x)}{\mathrm{A}(x)} = \frac{1}{1 - x} f(x)=A(x)B(x)=1−x1。
所以,我们找到了 f ( x ) f(x) f(x)的表达式,即 f ( x ) = 1 1 − x f(x) = \frac{1}{1 - x} f(x)=1−x1。
5. (10 分) 请用组合方法证明 ∑ k = 1 n C ( n , k ) k = n 2 n − 1 \sum_{k=1}^{n} C(n, \mathrm{k}) k=n 2^{n-1} ∑k=1nC(n,k)k=n2n−1
答:
∑
k
=
1
n
C
(
n
,
k
)
k
=
C
(
n
,
1
)
∗
1
+
C
(
n
,
2
)
∗
2
+
C
(
n
,
3
)
∗
3
+
⋯
+
C
(
n
,
k
)
∗
n
=
C
(
n
,
1
)
+
C
(
n
,
2
)
+
C
(
n
,
2
)
+
⋯
+
C
(
n
,
n
)
=
2
n
−
C
(
n
,
0
)
+
2
n
−
C
(
n
,
1
)
−
C
(
n
,
0
)
+
⋯
+
2
n
−
C
(
n
,
n
−
1
)
−
C
(
n
,
n
−
2
)
−
⋯
−
C
(
n
,
0
)
=
n
∗
2
n
−
(
n
∗
C
(
n
,
0
)
+
(
n
−
1
)
∗
C
(
n
,
1
)
+
⋯
+
C
(
n
,
n
−
1
)
)
=
n
∗
2
n
−
(
n
∗
C
(
n
,
n
)
+
(
n
−
1
)
∗
C
(
n
,
n
−
1
)
+
⋯
+
C
(
n
,
1
)
)
=
n
∗
2
n
−
∑
k
=
1
n
C
(
n
,
k
)
k
2
∗
∑
k
=
1
n
C
(
n
,
k
)
k
=
n
∗
2
n
\begin{array}{l} \sum_{k=1}^{n} C(n, \mathrm{k}) k=C(n, 1) * 1+C(n, 2) * 2+C(n, 3) * 3+\cdots+C(n, \mathrm{k}) * \mathrm{n} \\ =C(n, 1)+C(n, 2)+C(n, 2)+\cdots+C(n, n) \\ =2^{n}-C(n, 0)+2^{n}-C(n, 1)-C(n, 0)+\cdots+2^{n}-C(n, n-1) \\ -C(n, n-2)-\cdots-C(n, 0) \\ =n * 2^{n}-(n * C(n, 0)+(n-1) * C(n, 1)+\cdots+C(n, n-1)) \\ =n * 2^{n}-(n * C(n, n)+(n-1) * C(n, n-1)+\cdots+C(n, 1)) \\ =n * 2^{n}-\sum_{k=1}^{n} C(n, \mathrm{k}) k \\ 2 * \sum_{k=1}^{n} C(n, \mathrm{k}) k=n * 2^{n} \\ \end{array}
∑k=1nC(n,k)k=C(n,1)∗1+C(n,2)∗2+C(n,3)∗3+⋯+C(n,k)∗n=C(n,1)+C(n,2)+C(n,2)+⋯+C(n,n)=2n−C(n,0)+2n−C(n,1)−C(n,0)+⋯+2n−C(n,n−1)−C(n,n−2)−⋯−C(n,0)=n∗2n−(n∗C(n,0)+(n−1)∗C(n,1)+⋯+C(n,n−1))=n∗2n−(n∗C(n,n)+(n−1)∗C(n,n−1)+⋯+C(n,1))=n∗2n−∑k=1nC(n,k)k2∗∑k=1nC(n,k)k=n∗2n
即
∑ k = 1 n C ( n , k ) k = n ∗ 2 n − 1 \sum_{k=1}^{n} C(n, \mathrm{k}) k=n * 2^{n-1} ∑k=1nC(n,k)k=n∗2n−1
6. (10 分) 用数字 1,2,3 组成的长度为 n 的序列中,数字 1 出现了偶数次,且数字 2 出现了奇数次的序列有多少个?
答:
满足题目要求的指数型母函数为
g
(
x
)
=
(
1
+
x
2
2
!
+
x
4
4
!
+
⋯
)
(
x
+
x
3
3
!
+
x
5
5
!
+
⋯
)
(
1
+
x
+
x
2
2
!
+
x
3
3
!
+
x
4
4
!
+
⋯
)
=
(
e
x
+
e
−
x
2
)
∗
(
e
x
−
e
−
x
2
)
∗
e
x
=
1
4
(
e
3
x
−
e
−
x
)
=
1
4
∑
n
=
0
∞
(
3
n
−
(
−
1
)
n
)
x
n
n
!
1
4
(
3
n
−
(
−
1
)
n
)
个
\begin{array}{l} g(x)=\left(1+\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}+\cdots\right)\left(x+\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}+\cdots\right)\left(1+x+\frac{x^{2}}{2 !}+\frac{x^{3}}{3 !}+\frac{x^{4}}{4 !}+\cdots\right) \\ =\left(\frac{e^{x}+e^{-x}}{2}\right) *\left(\frac{e^{x}-e^{-x}}{2}\right) * e^{x} \\ =\frac{1}{4}\left(e^{3 x}-e^{-x}\right) \\ =\frac{1}{4} \sum_{n=0}^{\infty}\left(3^{n}-(-1)^{n}\right) \frac{x^{n}}{n !} \\ \frac{1}{4}\left(3^{n}-(-1)^{n}\right)_{\text {个 }} \end{array}
g(x)=(1+2!x2+4!x4+⋯)(x+3!x3+5!x5+⋯)(1+x+2!x2+3!x3+4!x4+⋯)=(2ex+e−x)∗(2ex−e−x)∗ex=41(e3x−e−x)=41∑n=0∞(3n−(−1)n)n!xn41(3n−(−1)n)个
7. (10 分)假设 A 是一个含有有限个元素的非空集合。证明 A 的含有奇数个元素的子集的个数等于含有偶数个元素的子集的个数。
答:
A 中含有 k 个元素的子集的数目是 C(n, k)=n ! / k !(n-k) ! ,则 A 的含有奇数个元素的子集个数等于 C(n, 1)+C(n, 3)+C(n, 5)+\ldots+C(n, n)
根据组合公司 C(n-1, k-1)+C(n-1, k)=C(n, k) ,有
C
(
n
−
1
,
0
)
+
C
(
n
−
1
,
1
)
=
C
(
n
,
1
)
C
(
n
−
1
,
2
)
+
C
(
n
−
1
,
3
)
=
C
(
n
,
3
)
…
…
C
(
n
−
1
,
2
k
)
+
C
(
n
−
1
,
2
k
+
1
)
=
C
(
n
,
2
k
+
1
)
\begin{array}{l} C(n-1,0)+C(n-1,1)=C(n, 1) \\ C(n-1,2)+C(n-1,3)=C(n, 3) \\ \ldots \ldots \\ C(n-1,2 k)+C(n-1,2 k+1)=C(n, 2 k+1) \end{array}
C(n−1,0)+C(n−1,1)=C(n,1)C(n−1,2)+C(n−1,3)=C(n,3)……C(n−1,2k)+C(n−1,2k+1)=C(n,2k+1)
两边相加得
C
(
n
−
1
,
0
)
+
C
(
n
−
1
,
1
)
+
C
(
n
−
1
,
2
)
+
C
(
n
−
1
,
3
)
+
…
+
C
(
n
−
1
,
2
k
)
+
C
(
n
−
1
,
2
k
+
1
)
=
C
(
n
,
1
)
+
C
(
n
,
3
)
+
…
+
C
(
n
,
2
k
+
1
)
\begin{array}{l} C(n-1,0)+C(n-1,1)+C(n-1,2)+C(n-1,3)+\ldots+C(n-1,2 k)+C(n-1,2 k+1)=C(n, 1)+ \\ C(n, 3)+\ldots+C(n, 2 k+1) \end{array}
C(n−1,0)+C(n−1,1)+C(n−1,2)+C(n−1,3)+…+C(n−1,2k)+C(n−1,2k+1)=C(n,1)+C(n,3)+…+C(n,2k+1)
另
2
k
+
1
=
n
2 \mathrm{k}+1=\mathrm{n}
2k+1=n ,有
(
1
+
1
)
n
−
1
=
C
(
n
,
1
)
+
C
(
n
,
3
)
+
⋯
+
C
(
n
,
n
)
2
n
−
1
=
C
(
n
,
1
)
+
C
(
n
,
3
)
+
⋯
+
C
(
n
,
n
)
\begin{array}{l} (1+1)^{n-1}=C(n, 1)+C(n, 3)+\cdots+C(n, n) \\ 2^{n-1}=C(n, 1)+C(n, 3)+\cdots+C(n, n) \end{array}
(1+1)n−1=C(n,1)+C(n,3)+⋯+C(n,n)2n−1=C(n,1)+C(n,3)+⋯+C(n,n)
同理可得 A \mathrm{A} A 的含有偶数个元素的子集个数也为 2 n − 1 2^{n-1} 2n−1 。即 A \mathrm{A} A 的含有奇数个元素的子集的个数等于含有偶数个元素的子集的个数。
8. (10 分) 会议室里有 n \mathbf{n} n 个人,会议开始前他们有些人相互握了手。请证明一定存在两个人,他们握手的次数相同。
答:
n
\mathrm{n}
n 个人,则每个人最多握手
n
−
1
\mathrm{n}-1
n−1 次。根据鸲笼原理,至少存在两个人,他们握手的次数相同。
9. (10 分) A、B、C、D、E、F 六名保安,要排一下国庆黄金周的值班工作。a 不能在周一值班, B 不能在周二值班,C 不能在周三值班,请问有多少种排法?
答: (2021 国考题)
A 在周一值班的排法有 5 种
B 在周二值班的排法有 5 ! 种
C 在周三值班的排法有 5 ! 种
A 在周一值班的排法,B 在周二值班的排法有 4 !
A
\mathrm{A}
A 在周一值班的排法,C 在周三值班的排法有 4 !
B 在周二值班的排法, C 在周三值班的排法有 4 !
A
\mathrm{A}
A 在周一值班的排法, B 在周二值班的排法, C 在周三值班的排法有 3 !
根据容斥原理,
6 !-3 * 5 !+3 * 4 !-3 !=720-360+72-6=426
即 a 不能在周一值班,B 不能在周二值班,C 不能在周三值班有 426 种排法
10. (10 分) 求 1 0 40 10^{40} 1040 和 2 0 30 20^{30} 2030 的公因子有多少个。
答:
1
0
40
=
2
40
∗
5
40
2
0
30
=
2
60
∗
5
30
\begin{array}{l} 10^{40}=2^{40} * 5^{40} \\ 20^{30}=2^{60} * 5^{30} \end{array}
1040=240∗5402030=260∗530
所以 1 0 40 和 2 0 30 的公因子有 C ( 41 , 1 ) ∗ C ( 31 , 1 ) = 1271 个 \text { 所以 } 10^{40} \text { 和 } 20^{30} \text { 的公因子有 } C(41,1) * C(31,1)=1271 \text { 个 } 所以 1040 和 2030 的公因子有 C(41,1)∗C(31,1)=1271 个
























 1372
1372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










