Hough 变换可以提取图像中的直线。但是提取的直线的精度不高。而很多场合下,我们需要精确的估计直线的参数,这时就需要进行直线拟合。
直线拟合的方法很多,比如一元线性回归就是一种最简单的直线拟合方法。但是这种方法不适合用于提取图像中的直线。因为这种算法假设每个数据点的X 坐标是准确的,Y 坐标是带有高斯噪声的。可实际上,图像中的每个数据点的XY 坐标都是带有噪声的。
下面就来讲讲适用于提取图像中直线的直线拟合算法。
一个点 (xi,yi) 到直线的距离用 ri 来表示。
所谓直线拟合,就是找到一条直线,使得:
最小。
ρ(r) 是距离函数。 ρ(r) 函数取不同的形式,对应不同的直线拟合方法。OpenCV 中支持 6 种不同的 ρ(r) 函数形式。分别是:
CV_DIST_L2
这种方法是以距离平方和为拟合判据。也就是常见的最小二乘拟合算法,运行速度也最快。但是这个算法也有个很大的问题,就是当干扰点离直线较远时,一个干扰点就可能将整条拟合直线拉偏了。简单的说就是对干扰点的鲁棒性不够。所以后来又提出了其他的函数。
CV_DIST_L1
CV_DIST_L12
CV_DIST_FAIR
其中 C = 1.3998
CV_DIST_WELSCH
其中 C = 2.9846
CV_DIST_HUBER
其中 C = 1.345
后面这 5 种函数我知道第一种,其他的不知道是怎么来的。OpenCV 的帮助文档给出了一个链接:M-estimator
但是这个页面也被墙了。
下面来说说 OpenCV 提供的直线拟合函数。函数原型如下:
- 1
- 2
- 3
- 4
- 5
- 6
- 1
- 2
- 3
- 4
- 5
- 6
distType 指定拟合函数的类型,可以取 CV_DIST_L2、CV_DIST_L1、CV_DIST_L12、CV_DIST_FAIR、CV_DIST_WELSCH、CV_DIST_HUBER。
param 就是 CV_DIST_FAIR、CV_DIST_WELSCH、CV_DIST_HUBER 公式中的C。如果取 0,则程序自动选取合适的值。
reps 表示直线到原点距离的精度,建议取 0.01。
aeps 表示直线角度的精度,建议取 0.01。
计算出的直线信息存放在 line 中,为 cv::Vec4f 类型。line[0]、line[1] 存放的是直线的方向向量。line[2]、line[3] 存放的是直线上一个点的坐标。
如果直线用 y=kx+b 来表示,那么 k = line[1]/line[0],b = line[3] - k * line[2]。
如果直线用 ρ=xcosθ+ysinθ 来表示, 那么 θ=arctank+π2
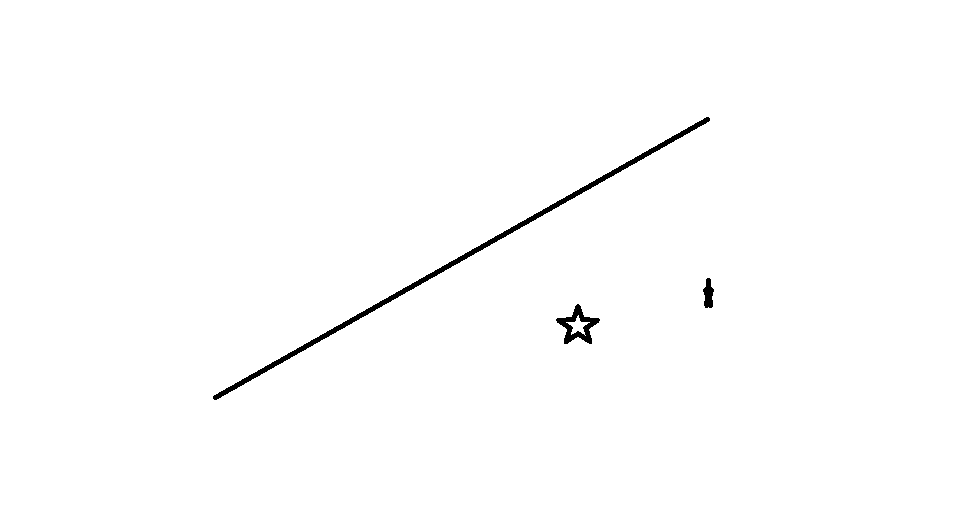
下面是个测试图像:
图像中有一条直线和一些干扰图案。
下面的代码可以从图像中提取出需要的坐标点。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
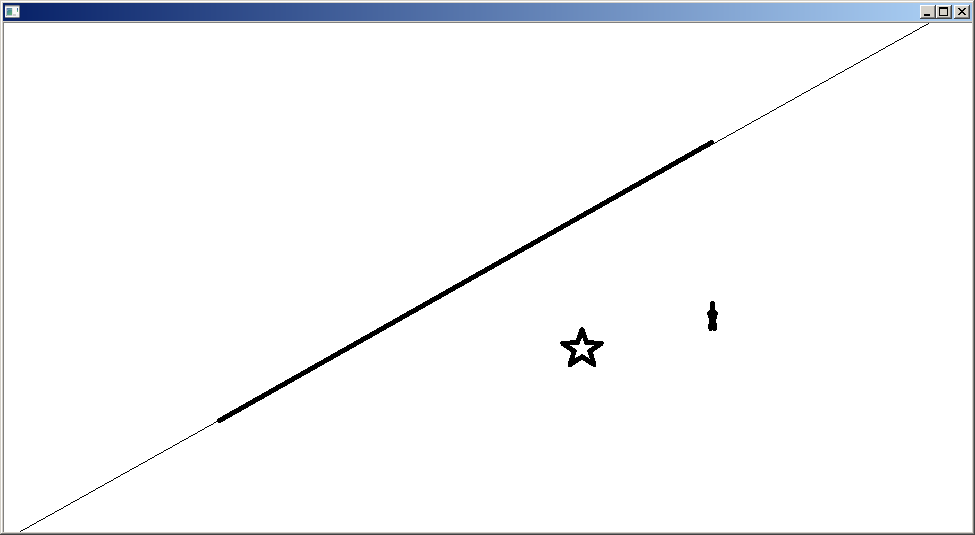
下面的代码可以在图中画一条直线。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
下面的代码是程序的主体。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
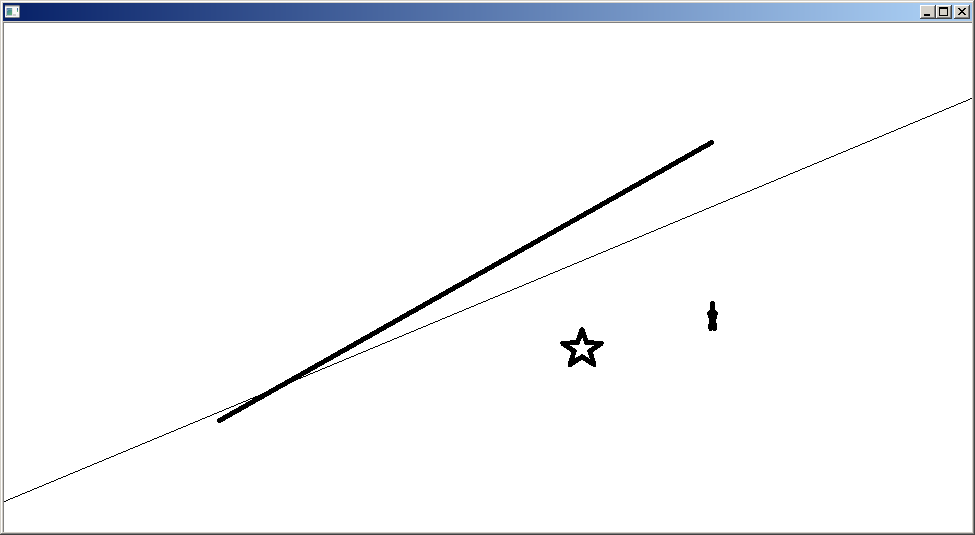
如果直线拟合类型选择 CV_DIST_L2。那么效果就没这么好了。代码不贴了,就贴个结果。






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








