这篇内容探讨了几何优化问题，包括寻找使PA+PB达到最小值的点P，涉及点在直线两侧或同侧的情况。同时，研究了在多条直线上寻找点P和Q以最小化PA+PQ+QB的路径，考虑了点的位置关系。此外，还讨论了如何在直线m上找到点P，使得PA+PB最短，以及在给定条件下的四边形周长最短问题。这些问题的解决方案利用了平移和对称性质，以及最短距离的概念。
一)、已知两个定点：
1、在一条直线m上，求一点P，使PA+PB最小；
(1)点A、B在直线m两侧：
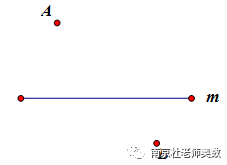
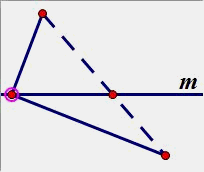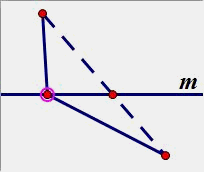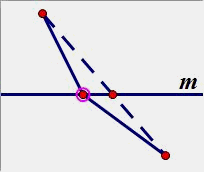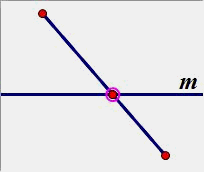
(2)点A、B在直线同侧：
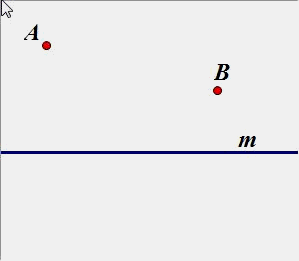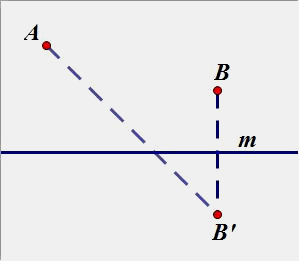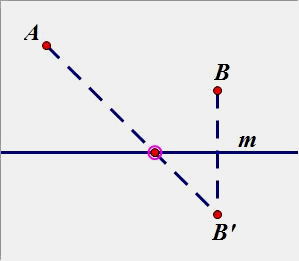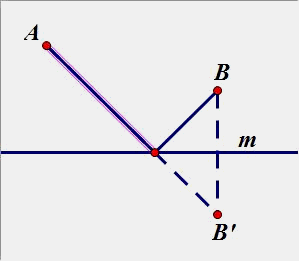
B、B’ 是关于直线m的对称点。
2、在直线m、n上分别找两点P、Q，使PA+PQ+QB最小。
(1)两个点都在直线外侧：
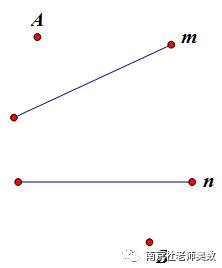
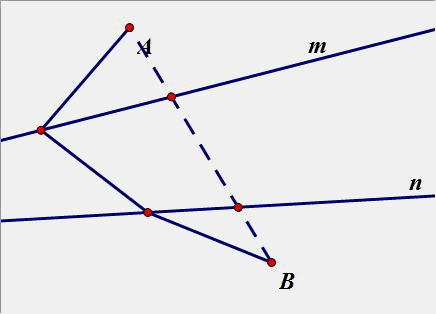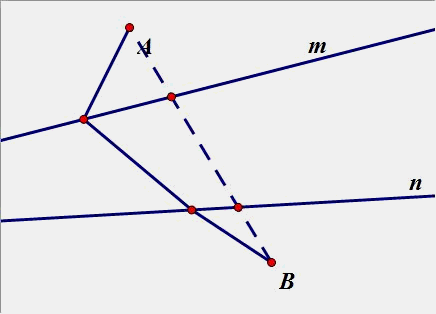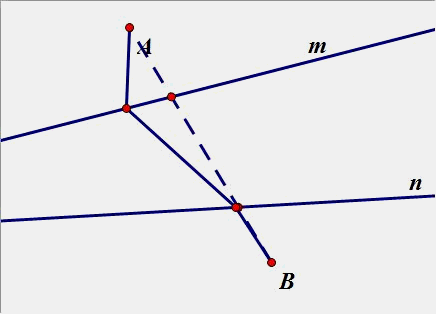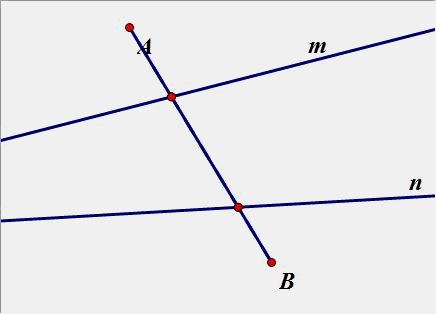
(2)一个点在内侧，一个点在外侧：
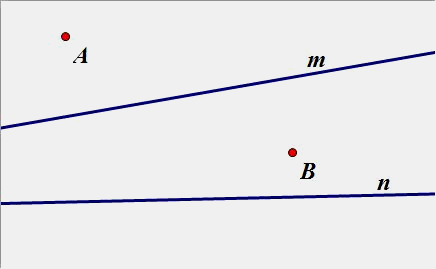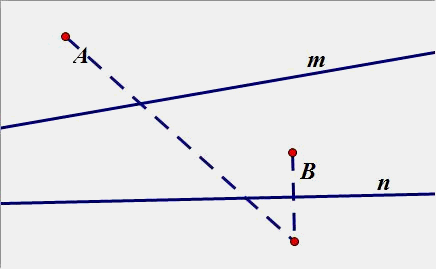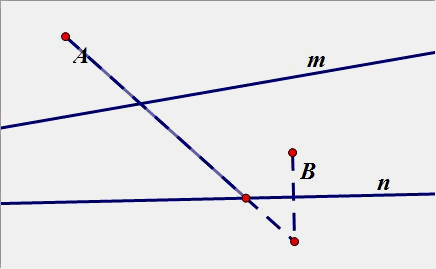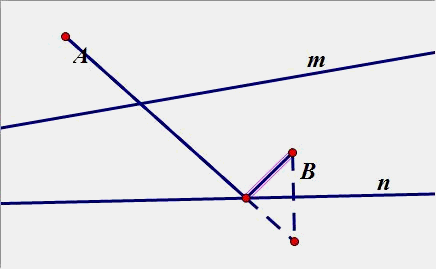
(3)两个点都在内侧：
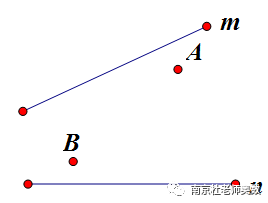
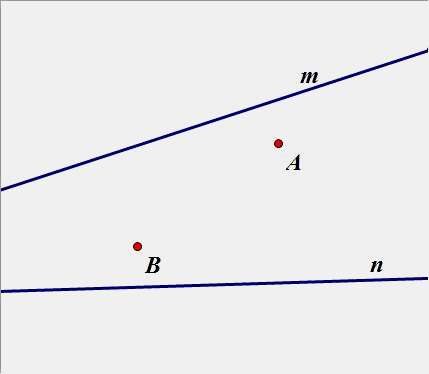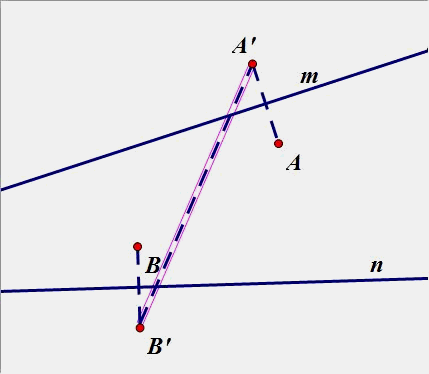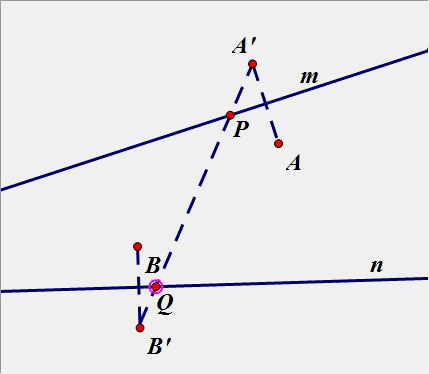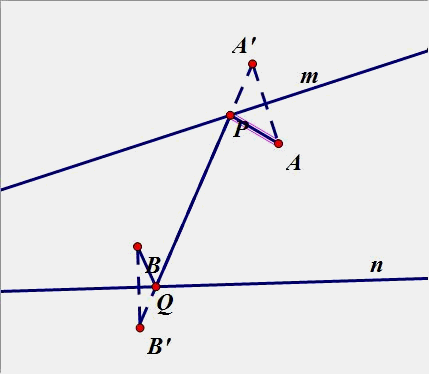
(4)、已知点A、B位于直线m,n 的内侧，在直线n、m分别上求点D、E点，使得围成的四边形ADEB周长最短.
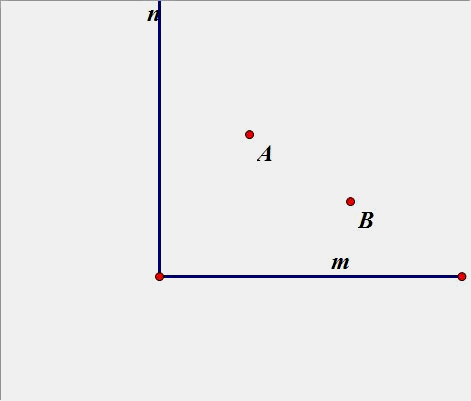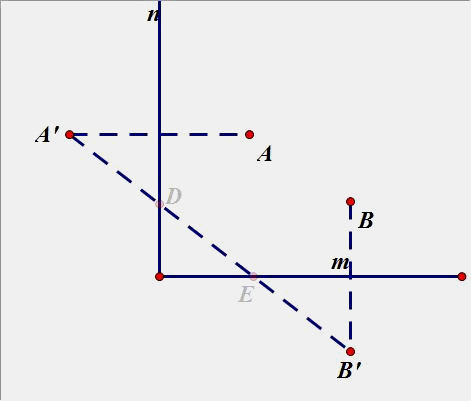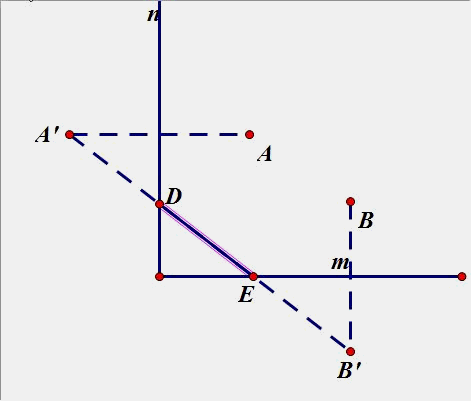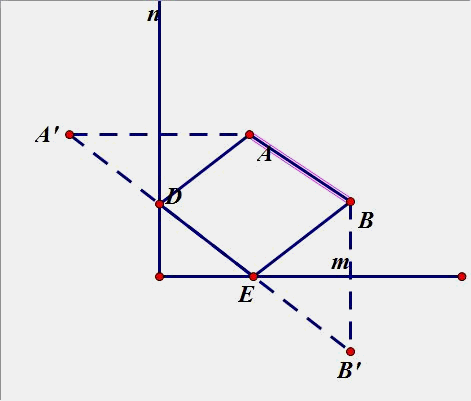
3.点B在直线n上运动，在直线m上找一点P，使PA+PB最小(在图中画出点P和点B)
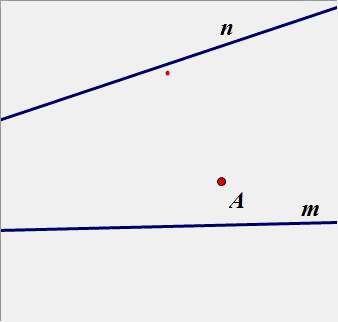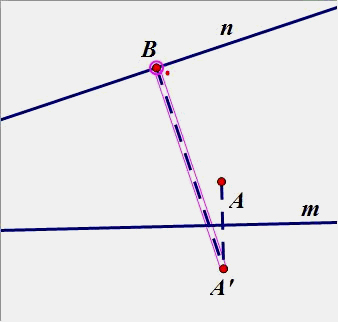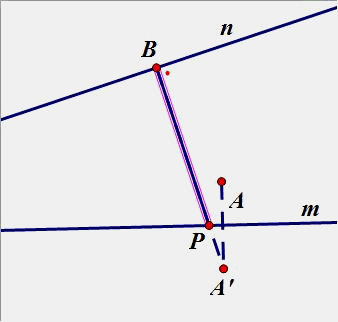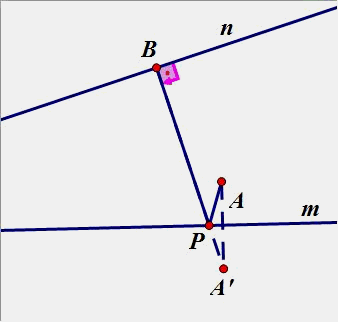
4.已知A、B是两个定点，P、Q是直线m上的两个动点，P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点，使得PA+PQ+QB的值最小。(原理用平移知识解)
(1)点A、B在直线m两侧：
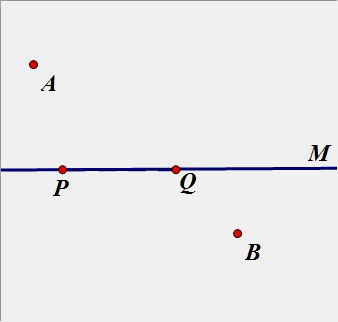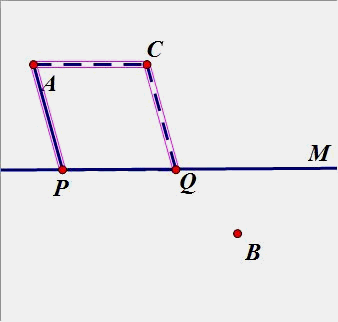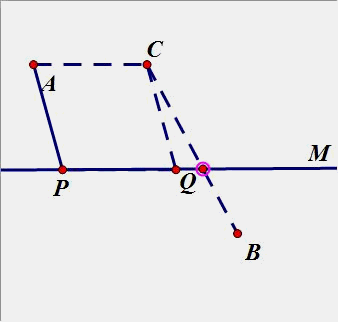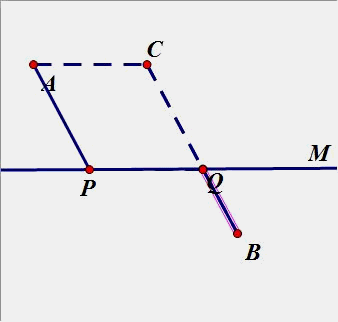
(2)点A、B在直线m同侧：
(4)如图，AB是2个定点,一个定长的C，在直线上取一个点P和Q，使得PQ等于定长C(P在Q的左边)，使得PA+PQ+QB的和最小。
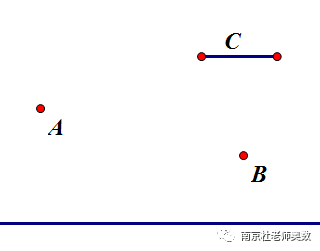
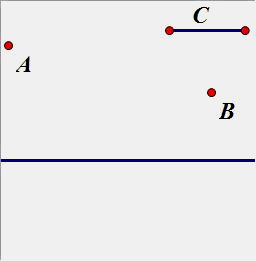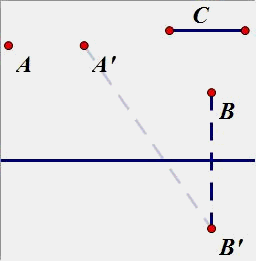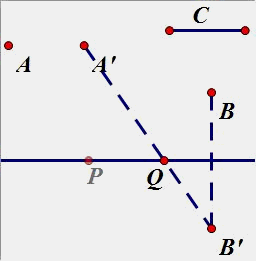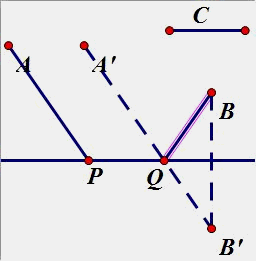
过点A找一条与直线平行的线段，使得线段与C等长。
(5)如图，AB两个村庄之间有一条河，要在河上架一座桥，桥的方向与河堤垂直，桥架何处才能使得A到B的距离最短？
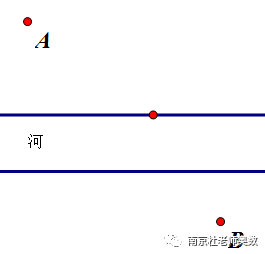
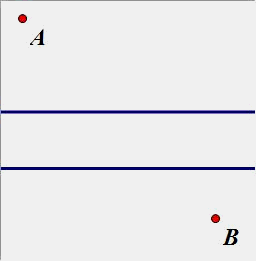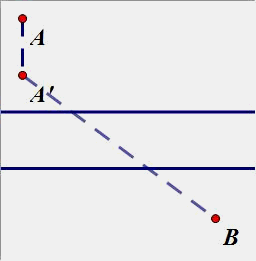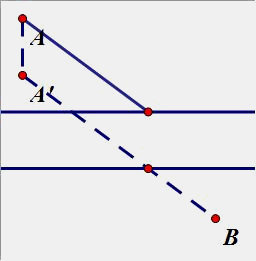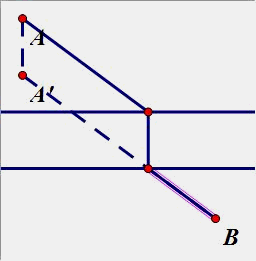
从点A作河边的垂线段，长度等于河宽即可
5. 如图，点A,B的距离是4，在一条直线上,求一点P，使|PA-PB|最大；最小呢？
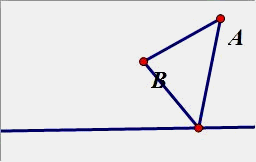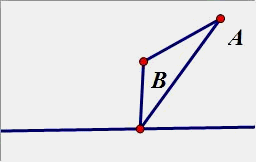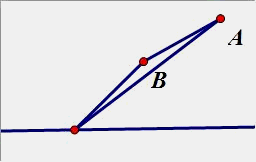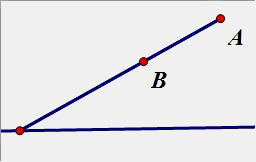
三角形的两边差小 于第三边，当3点成一线的时候，差等于第三边，最大为4，最小为0，
扫一扫
2396
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
