https://blog.csdn.net/roger__wong/article/details/41175967
浅层语义分析(LSA)是一种自然语言处理中用到的方法,其通过“矢量语义空间”来提取文档与词中的“概念”,进而分析文档与词之间的关系。LSA的基本假设是,如果两个词多次出现在同一文档中,则这两个词在语义上具有相似性。LSA使用大量的文本上构建一个矩阵,这个矩阵的一行代表一个词,一列代表一个文档,矩阵元素代表该词在该文档中出现的次数,然后再此矩阵上使用奇异值分解(SVD)来保留列信息的情况下减少矩阵行数,之后每两个词语的相似性则可以通过其行向量的cos值(或者归一化之后使用向量点乘)来进行标示,此值越接近于1则说明两个词语越相似,越接近于0则说明越不相似。
LSA最早在1988年由 Scott Deerwester, Susan Dumais, George Furnas, Richard Harshman, Thomas Landauer, Karen Lochbaum and Lynn Streeter提出,在某些情况下,LSA又被称作潜在语义索引(LSI)。
概述
词-文档矩阵(Occurences Matrix)
LSA 使用词-文档矩阵来描述一个词语是否在一篇文档中。词-文档矩阵式一个稀疏矩阵,其行代表词语,其列代表文档。一般情况下,词-文档矩阵的元素是该词在文档中的出现次数,也可以是是该词语的tf-idf(term frequency–inverse document frequency)。
词-文档矩阵和传统的语义模型相比并没有实质上的区别,只是因为传统的语义模型并不是使用“矩阵”这种数学语言来进行描述。
降维
在构建好词-文档矩阵之后,LSA将对该矩阵进行降维,来找到词-文档矩阵的一个低阶近似。降维的原因有以下几点:
- 原始的词-文档矩阵太大导致计算机无法处理,从此角度来看,降维后的新矩阵式原有矩阵的一个近似。
- 原始的词-文档矩阵中有噪音,从此角度来看,降维后的新矩阵式原矩阵的一个去噪矩阵。
- 原始的词-文档矩阵过于稀疏。原始的词-文档矩阵精确的反映了每个词是否“出现”于某篇文档的情况,然而我们往往对某篇文档“相关”的所有词更感兴趣,因此我们需要发掘一个词的各种同义词的情况。
降维是对原有矩阵的行数进行减少,后面采用SVD选取k阶最大的特征值,得到降维之后的Xk
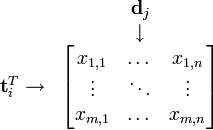
可以看到,每一行代表一个词的向量,该向量描述了该词和所有文档的关系。
相似的,一列代表一个文档向量,该向量描述了该文档与所有词的关系。
词向量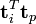 的点乘可以表示这两个单词在文档集合中的相似性。矩阵
的点乘可以表示这两个单词在文档集合中的相似性。矩阵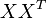 包含所有词向量点乘的结果,元素(i,p)和元素(p,i)具有相同的值,代表词p和词i的相似度。类似的,矩阵
包含所有词向量点乘的结果,元素(i,p)和元素(p,i)具有相同的值,代表词p和词i的相似度。类似的,矩阵 包含所有文档向量点乘的结果,也就包含了所有文档那个的相似度。
包含所有文档向量点乘的结果,也就包含了所有文档那个的相似度。
现在假设存在矩阵 的一个分解,即矩阵
的一个分解,即矩阵 可分解成正交矩阵U和V,和对角矩阵
可分解成正交矩阵U和V,和对角矩阵 的乘积。
的乘积。
这种分解叫做奇异值分解(SVD),即:

因此,词与文本的相关性矩阵可以表示为:
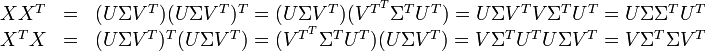
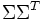 与
与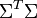 是对角矩阵,因此
是对角矩阵,因此 肯定是由
肯定是由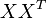 的特征向量组成的矩阵,同理
的特征向量组成的矩阵,同理 是
是 特征向量组成的矩阵。这些特征向量对应的特征值即为
特征向量组成的矩阵。这些特征向量对应的特征值即为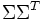 中的元素。综上所述,这个分解看起来是如下的样子:
中的元素。综上所述,这个分解看起来是如下的样子:
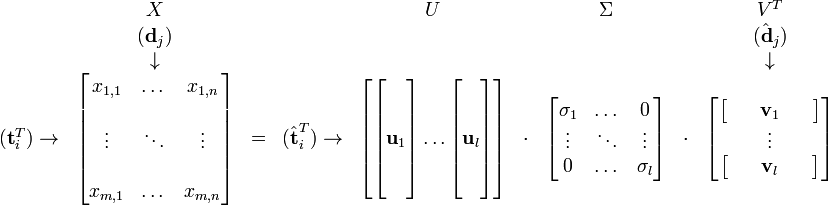
 被称作是奇异值,而
被称作是奇异值,而  和
和 则叫做左奇异向量和右奇异向量。通过矩阵分解可以看出,原始矩阵中的
则叫做左奇异向量和右奇异向量。通过矩阵分解可以看出,原始矩阵中的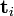 只与U矩阵的第i行有关,我们则称第i行为
只与U矩阵的第i行有关,我们则称第i行为  。同理,原始矩阵中的
。同理,原始矩阵中的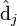 只与
只与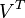 中的第j列有关,我们称这一列为
中的第j列有关,我们称这一列为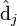 。
。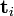 与
与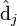 并非特征值,但是其由矩阵所有的特征值所决定。
并非特征值,但是其由矩阵所有的特征值所决定。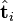 与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。同理,向量
与含有k个奇异值的矩阵相乘,实质是从高维空间到低维空间的一个变换,可以理解为是一个高维空间到低维空间的近似。同理,向量 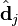 也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
也存在这样一个从高维空间到低维空间的变化。这种变换用公式总结出来就是这个样子:
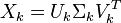
- 判断文档相似度:比较V的列,判断文档
 与
与  在低维空间的相似度。比较向量
在低维空间的相似度。比较向量 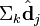 与向量
与向量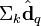 (比如使用余弦夹角)即可得出。
(比如使用余弦夹角)即可得出。 - 判断词的相似度:比较U的行,通过比较
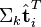 与
与 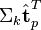 可以判断词
可以判断词 和词
和词 的相似度。
的相似度。 - 有了相似度则可以对文本和文档进行聚类。
- 给定一个查询字符串,算其在语义空间内和已有文档的相似性。

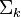 的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
的逆矩阵可以通过求其中非零元素的倒数来简单的得到。
 将其映射到语义空间,再与文档进行比较。
将其映射到语义空间,再与文档进行比较。
低维的语义空间可以用于以下几个方面:
- 在低维语义空间可对文档进行比较,进而可用于文档聚类和文档分类。
- 在翻译好的文档上进行训练,可以发现不同语言的相似文档,可用于跨语言检索。
- 发现词与词之间的关系,可用于同义词、歧义词检测。.
- 通过查询映射到语义空间,可进行信息检索。
- 从语义的角度发现词语的相关性,可用于“选择题回答模型”(multi choice qustions answering model)。








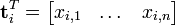

















 1249
1249

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








