Python实现P-PSO优化算法优化支持向量机SVR回归模型项目实战

说明：这是一个机器学习实战项目（附带数据+代码+文档+视频讲解），如需数据+代码+文档+视频讲解可以直接到文章最后关注获取。

1.项目背景

在当今数据驱动的时代，机器学习技术已经成为解决复杂问题的重要工具。支持向量机（SVM）作为一种经典的机器学习算法，在分类和回归任务中表现出色，尤其是其变体支持向量回归（SVR），在处理非线性数据时具有显著优势。然而，SVR模型的性能高度依赖于超参数的选择，如正则化参数 (C)、核参数 (gamma) 等。这些超参数的选择直接影响模型的预测精度和泛化能力，因此如何高效地优化这些超参数成为提升模型性能的关键。

近年来，基于群体智能的优化算法因其全局搜索能力和鲁棒性而受到广泛关注。粒子群优化（PSO）算法是一种受自然界群体行为启发的元启发式算法，能够快速探索解空间并找到近似最优解。P-PSO（Phase-based Particle Swarm Optimization）是PSO的一种改进版本。将P-PSO应用于SVR模型的超参数优化，不仅可以提高模型性能，还能为复杂的机器学习任务提供一种高效的解决方案。P-PSO 可以称为 相量粒子群优化算法，强调其在粒子群优化中引入了相量的概念以改进搜索性能。

本项目旨在结合P-PSO优化算法与SVR回归模型，针对实际数据集进行超参数优化和模型训练。通过对比传统网格搜索和随机搜索方法，验证P-PSO在超参数优化中的优越性，并探索其在不同数据分布和噪声条件下的适应性。最终目标是构建一个高效、可靠的回归预测系统，为工业生产、金融分析或环境监测等领域的实际应用提供技术支持。

本项目通过Python实现P-PSO优化算法优化支持向量机SVR回归模型项目实战。           

2.数据获取

本次建模数据来源于网络(本项目撰写人整理而成)，数据项统计如下：

编号	变量名称	描述
1	x1
2	x2
3	x3
4	x4
5	x5
6	x6
7	x7
8	x8
9	x9
10	x10
11	y	因变量

数据详情如下(部分展示)：

3.数据预处理

3.1 用Pandas工具查看数据

使用Pandas工具的head()方法查看前五行数据：

关键代码：

3.2数据缺失查看

使用Pandas工具的info()方法查看数据信息：

从上图可以看到，总共有11个变量，数据中无缺失值，共2000条数据。

关键代码： 

3.3数据描述性统计

通过Pandas工具的describe()方法来查看数据的平均值、标准差、最小值、分位数、最大值。

关键代码如下：  

4.探索性数据分析

4.1 y变量分布直方图

用Matplotlib工具的hist()方法绘制直方图：

4.2 相关性分析

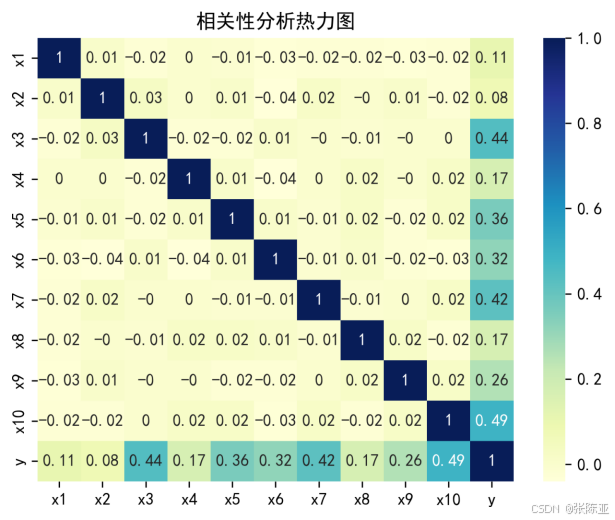
从上图中可以看到，数值越大相关性越强，正值是正相关、负值是负相关。  

5.特征工程

5.1 建立特征数据和标签数据

关键代码如下：

5.2 数据集拆分

通过train_test_split()方法按照80%训练集、20%测试集进行划分，关键代码如下： 

5.3 数据归一化

数据归一化关键代码如下：

6.构建P-PSO优化算法优化支持向量机SVR回归模型   

主要使用通过P-PSO优化算法优化支持向量机SVR回归模型，用于目标回归。       

6.1 寻找最优参数值 

最优参数值： 

   

6.2 最优参数构建模型 

编号	模型名称	参数
1	SVM回归模型	C=best_C
2		gamma=best_gamma
3		epsilon=best_epsilon

7.模型评估

7.1评估指标及结果  

评估指标主要包括R方、均方误差、解释性方差、绝对误差等等。

模型名称	指标名称	指标值
测试集
SVM回归模型	R方	0.9527
	均方误差	0.001
	解释方差分	0.9672
	绝对误差	0.0263

从上表可以看出，R方分值为0.9527，说明模型效果比较好。    

关键代码如下：     

7.2 真实值与预测值对比图

从上图可以看出真实值和预测值波动基本一致，模型效果良好。       

8.结论与展望

综上所述，本文采用了Python实现P-PSO优化算法优化支持向量机SVR回归算法来构建回归模型，最终证明了我们提出的模型效果良好。此模型可用于日常产品的预测。