【三维重建】对极几何

Patrick star`

已于 2024-01-24 16:48:04 修改

阅读量630

点赞数 7

文章标签：数码相机

于 2023-12-11 16:41:50 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/holle_world_ldx/article/details/134811917

版权

基础矩阵与本质矩阵

极几何描述了同一场景或者物体的两个视点图像间的几何关系

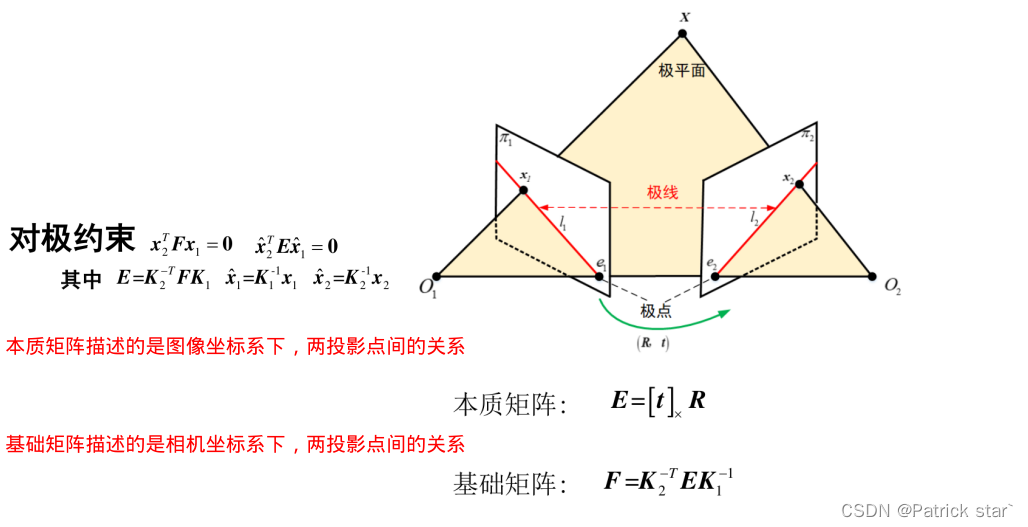
公式推导：

基础矩阵具有以下几种性质：

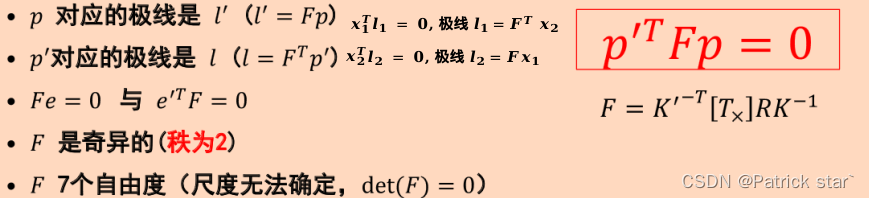
求解基础矩阵

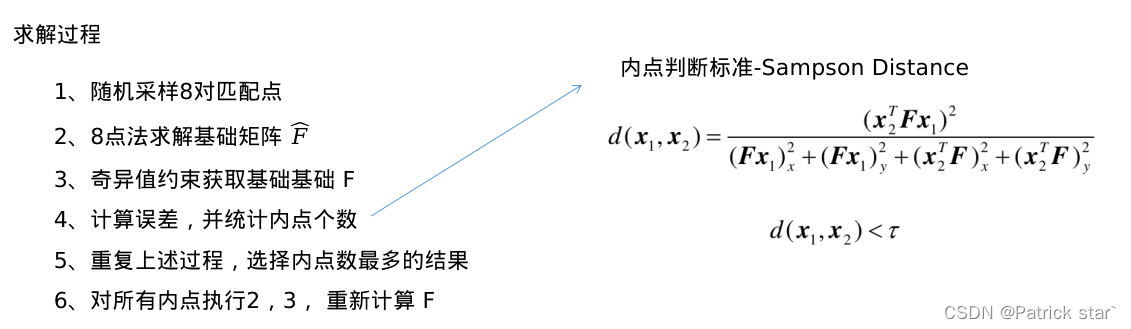
8点法求解基础矩阵

用对应点求解Ｆ

求出的 $\hat{F}$ 往往是满秩的，而我们所要求的基础矩阵秩为２

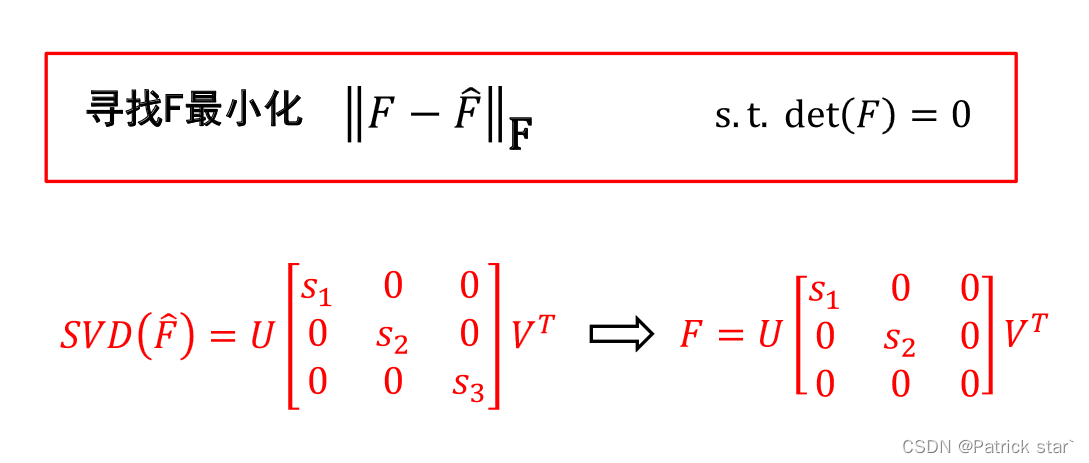
RANSAC求解基础矩阵

单应性矩阵

如果采集到的对应点在同一平面，用8点法求基础矩阵时，列出的方程组是线性相关，无法求解。

因此，如果采集到的对应点在同一平面，两个视点间的对应关系用单应性矩阵表示。

在实际使用中，并不知道匹配的对应点十分是同一平面

一般情况下，基础矩阵和单应性矩阵都会求，看谁的重投影误差小。

$M = K(I \ O),\ M' = K'(I\ O),\ P= (\tilde{P^T},1)^T \\ \\ p = M\begin{pmatrix} \tilde{P}\\1 \end{pmatrix} =K \tilde{P} \\ \\ p' = M'\begin{pmatrix} \tilde{P}\\1 \end{pmatrix}=K'(R \ t)\begin{pmatrix} \tilde{P} \\1 \end{pmatrix}=K'(R \tilde{P} + t)$

$n^T \tilde{P} = d \rightarrow n^T \tilde{P} / d = 1 \\ \\ let \ n / d = n_d , n_d^T \tilde{P} = 1$

$p'=K'(R\tilde{P} + t \cdot n_d^T \tilde{P}) = K'(R + t \cdot n_d^T)\tilde{P} =K'(R + t \cdot n_d^T)K^{-1}p$

$H = K'(R + t \cdot n_d^T)K^{-1}$

$p' = Hp$

C++代码实现：https://github.com/ldx-star/Epipolar-Geometry.git

关注

7
点赞
踩
9

收藏

觉得还不错? 一键收藏
0
评论
【三维重建】对极几何

可以发现Ｐ在左右相机的投影点一定在各自的极线上，如果求出极线就能缩小求解对应点的范围。基础矩阵对一般的透视摄像机的两个视点的图像间的极几何关系进行代数描述。本质矩阵对规范化摄像机拍摄的两个视点图像间的极几何关系进行代数描述。如果采集到的对应点在同一平面，两个视点间的对应关系用单应性矩阵表示。极几何描述了同一场景或者物体的两个视点图像间的几何关系。E就是本质矩阵，描述了规范化摄像机下两个视点的关系。F就是基础矩阵，反映了一般相机下，两视点间的关系。规范化相机指的是相机的内参矩阵为一个单位矩阵。
复制链接

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。