本文介绍了命题的基本概念，包括命题的定义、命题连接词及其使用场景，并详细解析了命题公式的分类和真值表等内容。
命题
命题必须符合两个要求： 1、是陈述句 2、能够判断真假（可以不知道真假）
命题连接词
如下表：
否定
不用多说 P为真 非P就为假 反之同理
合取 “既...又...” “当且仅当”
如：小明既是大学生，也是运动员。
若小明不是大学生，也不是运动员，那么此命题自然是假！
析取 “或”（严格来说析取代表的是“同或”
蕴涵 P为前件 Q为后件
如：如果周末天气好，那么我们就去郊游
ps：当前件为假的时候，这个命题不太好判断，因为天气不好，那么你去不去郊游，都无法拿来判断“如果周末天气好，那么我们就去郊游”这句话的真假
所以我们规定，前件为假的时候，后件不管是啥，我们都说这个命题是真（这就是 善意推定）
ps：如果有犯罪证据，那么他就有罪。（如果没证据呢，那么无论他有没有罪，我们都认为他无罪，疑罪从无，善意推定）
等价 “当且仅当”
真值表总结：
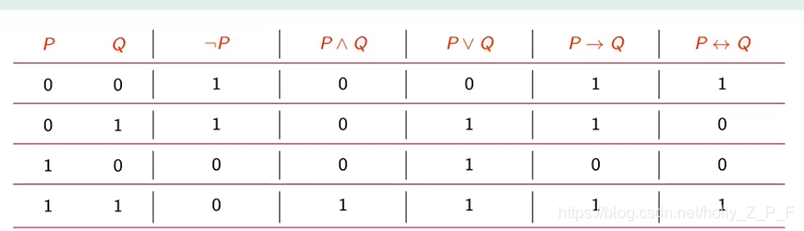
联结词的优先级：
命题符号化
公式的解释
一个命题 P 我们不知道他是真还是假，所以称它为命题变元
假设一个命题公式包含n个命题变元
我们给每一个变元赋一个值：L1：P1 真 P2 假 P3 真 P4 假 .........那么L1就是命题公式的一个解释
一个命题公式有n个不同的命题变元，那么就有2的n次方个解释。
而公式G在所有可能的解释下所取得的真值，就是G的真值表。
命题公式分类：
如果一个公式在其所有解释下都为真，成为永真公式（重言式）
如果一个公式在其所有解释下都为假，成为永假公式（矛盾式）
一个公式，不是永假的，那就是可满足公式
（永假公式也叫不可满足公式）
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
