【论文翻译】Image Super-Resolution Using Deep Convolutional Networks

论文理解

这篇文章是使用深度学习进行图像超分辨率重建的开山之作。
这篇文章提出了一个用于单源图像超分辨率重建的网络模型SRCNN，对比了传统重建方法，评估了该模型的性能。
该模型大致结构如下图：
（这是我根据理解自己画的图，并非论文里的图，所以不一定对，可能有误）

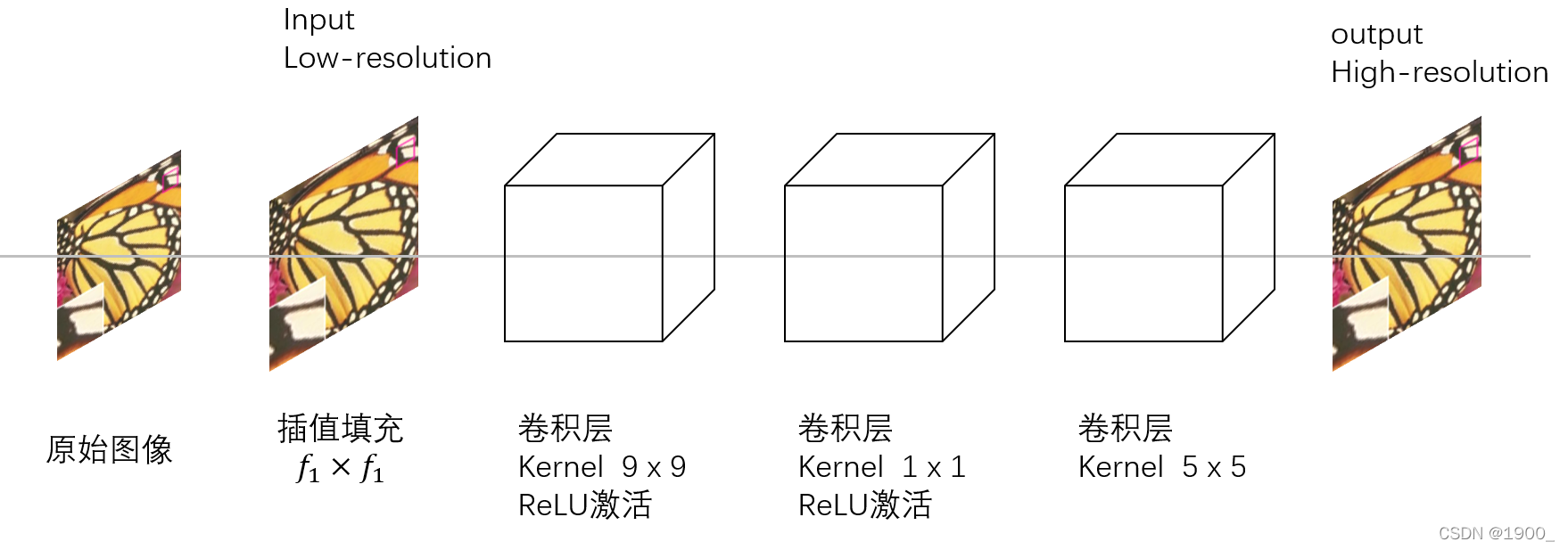
以下是论文部分翻译：

1.INTRODUCTION

单一图像的超分辨率（SR，super-resolution ），旨在从单一的低分辨率图像中恢复出高分辨率的图像，是计算机视觉中的一个经典问题。这个问题本质上是不成立的（ill-posed），因为对于任何给定的低分辨率像素，都存在多种解决方案。

换句话说，这是一个欠定的（underdetermined）逆向问题，其解决方案不是唯一的。这样的问题通常是通过强有力的先验信息来约束解空间来缓解的。为了学习先验信息，目前最先进的方法大多采用基于实例（example-based）的策略[44]。这些方法要么利用同一图像的内部相似性，要么基于外部低分辨率图像和高分辨率图像组成的样本对（exemplar pairs）之间的映射函数（mapping functions）。基于外部实例的方法可以为一般的图像超分辨率而制定，也可以根据提供的训练样本，设计成适合特定领域的任务，例如：人脸幻想（face hallucination）。

基于稀疏编码(sparse-coding-based, SC)方法，是基于外部实例的SR方法中具有代表性的方法之一。此方法涉及其解决流程中的几个步骤。首先，从输入图像中密集裁剪出重叠的小块并进行预处理（减去均值和归一化）。然后用一个低分辨字典对这些图像块进行编码。得到稀疏系数，再利用高分辨率字典重建对应的高分辨率图像块，最后对这些重叠的重构图像块（reconstructed patches）进行组合（例如权值平均）得到最终的输出。这个流程（pipeline）被大多数外部基于实例的方法共享，它们特别注意学习和优化字典，或者构建高效的映射函数。然而，这个流程中的其他步骤很少被优化或者在一个统一的优化框架中考虑。

在本文中，我们证明了上述处理流程等价于深度卷积神经网络。基于这一事实，我们考虑一种卷积神经网络，它可以直接学习低分辨率和高分辨率图像之间的端到端映射。我们的方法与现有的基于外部例子的方法有很大的不同，我们的方法没有明确地学习字典或为图片空间(patch space)建模。这些都是通过隐藏层隐含实现的。此外，图像(patch)的提取和聚集也被表述为卷积层，所以也参与了优化。在我们的方法中。 整个SR解决流程完全通过学习获得，几乎没有前/后处理。我们将提出的模型命名为超分辨率卷积神经网络(SRCNN，super-resolution convolutional neural network)

SRCNN有几个特点：首先，它的结构被有意地设计得简单，但与最先进的基于实例的方法相比，它提供了更高的准确性。其次，适度数量的filter和layer，我们的方法达到快速的实际在线使用，即使在CPU上。我们的方法比许多基于实例的方法更快，因为它是完全前馈的（fully feed-forward），在使用上不需要解决任何优化问题。第三，实验表明，(i)数据集更大、更多样化时，(ii)使用更大、更深入的模型时，网络的恢复质量可以进一步提高。相反，更大的数据集/模型会给现有的基于实例的方法带来挑战。此外，该网络可以同时处理三通道彩色图像，以提高超分辨率性能。总体而言，本研究的贡献主要体现在三个方面:

（1）我们提出了一个全卷积神经网络的图像超分辨率。该网络直接学习低分辨率和高分辨率图像之间的端到端映射，除了优化外，几乎没有预处理/后处理。（2）我们建立了基于深度学习的SR方法与传统的基于稀疏编码的SR方法之间的关系。这种关系为网络结构的设计提供了指导。（3）我们证明了深度学习在经典的超分辨率计算机视觉问题中是有用的，并且可以获得良好的质量和速度。

这项工作的早期版本已经发布，我们这次在之前的基础上做了改动：首先，我们通过在非线性映射层中引入更大的滤波器（filter）尺寸来改进SRCNN，并通过添加非线性映射层来探索更深层次的结构。其次，扩展了SRCNN，能同时处理三个颜色通道(YCbCr或RGB颜色空间);实验表明，与单通道网络相比，该网络的性能得到了改善。第三，在最初的结果中加入了大量新的分析和直观的解释。我们也扩充了原始实验的数据集。此外，我们比较了一些最近发布的方法，并确认我们的模型仍然优于使用不同评估指标的现有方法。

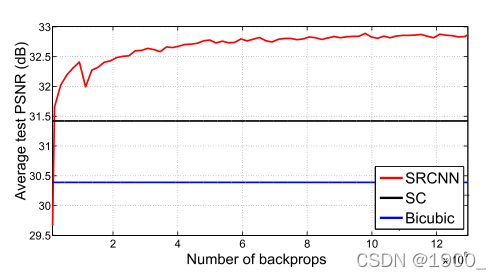
三种方法的对比。所提出的超分辨率卷积神经网络仅经过少量的训练迭代就超过了Bicubic，在适度训练的情况下，其性能优于sparse-coding-based方法。更多的训练迭代可以进一步提高性能。

2.RELATED WORK

2.1 Image Super-Resolution

According to the image priors, single-image super resolution algorithms can be categorized into four types—prediction models, edge based methods, image statistical methods and patch based (or example-based) methods.

根据图像的先验知识，单图像超分辨率算法可分为四种类型:预测模型、基于边缘的方法、图像统计方法和基于patch(或基于实例)的方法。

2.1这一节主要就是介绍了一些现有的研究成果以及方法的局限性。

2.2 Convolutional Neural Networks (CNN)

卷积神经网络的广泛应用得益于三个因素：（1）GPU的加速（2）ReLU的提出（3）丰富的数据集

2.3 Deep Learning for Image Restoration

介绍了一些深度学习用来图像恢复的研究

3.CONVOLUTIONAL NEURAL NETWORKS FOR SUPER-RESOLUTION

3.1 Formulation

考虑一个低分辨率的图像，我们首先使用bicubic插值将其提升到所需的大小，这是我们执行的唯一预处理。得到的图像我们用Y表示，我们的目标是从Y重建一幅高分辨图像F(Y)，使其尽可能于高分率真值图像X相似。为了便于表达，我们仍然称Y为“低分辨率”图像，尽管它与x的大小相同。我们希望学习映射F，它在概念上包含三个操作:

（1）图像块（ Patch）的提取和表示：该操作从低分辨率图像Y中提取(重叠的)patch，并将每个patch表示为高维向量。这些向量构成一组特征图，特征图的个数等于向量的维数。（2）非线性映射：这个操作将每个高维向量非线性地映射到另一个高维向量上。每个映射向量在概念上表示一个高分辨率的patch。这些向量构成了另一组特征图。（3）重建：该操作将上述高分辨率的patch-wise表示集合起来，生成最终的高分辨率图像。这个图像被期望与真值X相似。

这三个操作构成一个卷积神经网络。如图所示：
（这是我根据自己理解画的图，不是文章里的图哈，也不一定对，可能有误）

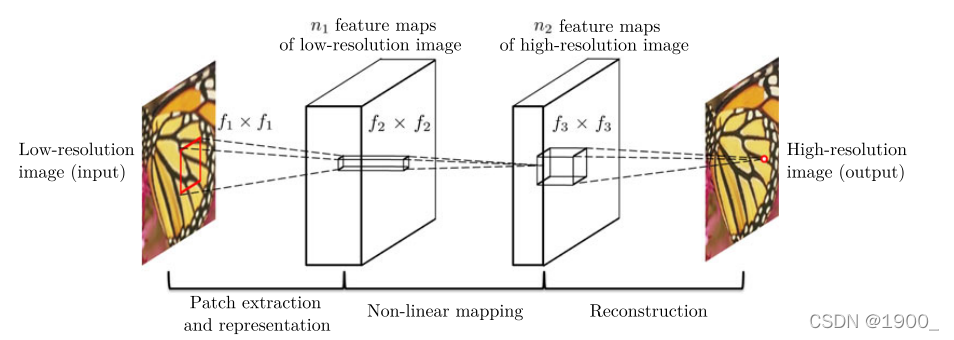
给定一个低分辨率的图像Y, SRCNN的第一卷积层提取一组特征图。第二层将这些特征映射非线性地映射到高分辨率的patch表示。最后一层结合了一个空间区域内的预测，生成最终的高分辨率图像F(Y)。

3.1.1 Patch Extraction and Representation

一种流行的图像恢复策略是密集提取小块，然后用一组预先训练的基(如PCA、DCT、Haar等)表示它们。这相当于用一组滤波器对图像进行卷积，每个滤波器都是一组基。在我们的公式中，我们将这些基的优化纳入到网络的优化中。形式上，我们的第一层被表示为一个操作$F_1$:
$$F_1(Y)=max(0,W_1\ast Y+B_1)$$
其中，W1和B1分别表示滤波器和偏置，*表示卷积。这里$W_1$对应$n_1$个filter，每个filter是$c\times f_1\times f_1$，c是通道数，$f_1$是滤波器尺寸。经过卷积之后我们就得到$n_1$个特征图。接着我们对卷积结果应用ReLU（$max(0,x)$）。

3.1.2 Non-Linear Mapping

第一层为每个patch提取一个$n_1$维的特征。在第二个运算中，我们将每个$n_1$维的向量映射为一个$n_2$维的向量。这等价于使用$n_2$个滤波器，其中每个滤波器只对应$1\times 1$的空间位置。当然这种解释只适用于尺寸$1\times 1$的滤波器。但是对于大的滤波器，$3\times 3$，$5\times 5$，非线性映射不是对应图像块，而是对应特征图中的 $3\times 3$ ,$5\times 5$“块”。这一步可以看做下面的卷积
$$F_2(Y)=max(0,W_2\ast F_1(Y)+B_2)$$
其中 $W_2$包含 $n_2$个滤波器，每个尺寸是 $n_1\times f_2\times f_2$。这样就得到了一个 $n_2$维向量，对应高分辨率图像块。我们可以添加更多的卷积层来增加非线性。但这可能会增加模型的复杂性（一层的参数是$n_2\times f_2\times f_2\times n_2$），因此需要更多的训练时间。

3.1.3 Reconstruction

在传统的方法中，通常将预测的重叠高分辨率图像块进行平均，得到最终的完整图像。这个平均操作你可以看作是对一组特征图（ feature maps）的一个预先定义的滤波器（predefined filter ）。（每个位置都是高分辨图像块的展平（flattened）形式），基于此，我们定义了一个卷积层来生成最终的高分辨率图像:
$$F(Y)=W_3\ast F_2(Y)+B_3$$
这里的$W_3$对应的是$c$个filter大小为$n_2\times f_3\times f_3$，$B_3$是一个c维的vector。

我们将这三种操作放在一起，形成一个卷积神经网络。在这个模型中，我们将对所有的滤波权值和偏差进行优化。

3.2 Relationship to Sparse-Coding-Based Methods

这一节将的是，基于稀疏编码（sparse-coding-based）的方法可以被证明等价于一个卷积神经网络。

3.3 Training

Loss函数采用MSE（Mean Squared Error ，均方差）。利用随机梯度下降（stochastic gradient descent）和标准反向传播（standard backpropagation）来最小化Loss。

4.EXPERIMENTS

4.1 Training Data

作为对比，我们使用了一个较小的训练集（91张图），和一个较大的训练集（来自ILSVRC2013 ImageNet detection partition的395909张图）。性能对比如下：

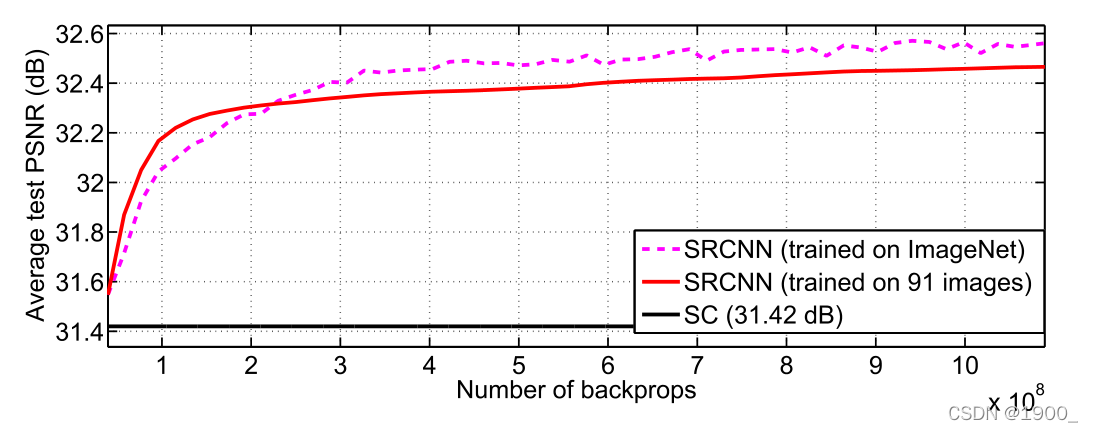
4.2 Learned Filters for Super-Resolution

如图是以放大因子3在ImageNet上训练时，学习出的第一层滤波器（filter）的示例。

下图是不同的层的特征图：

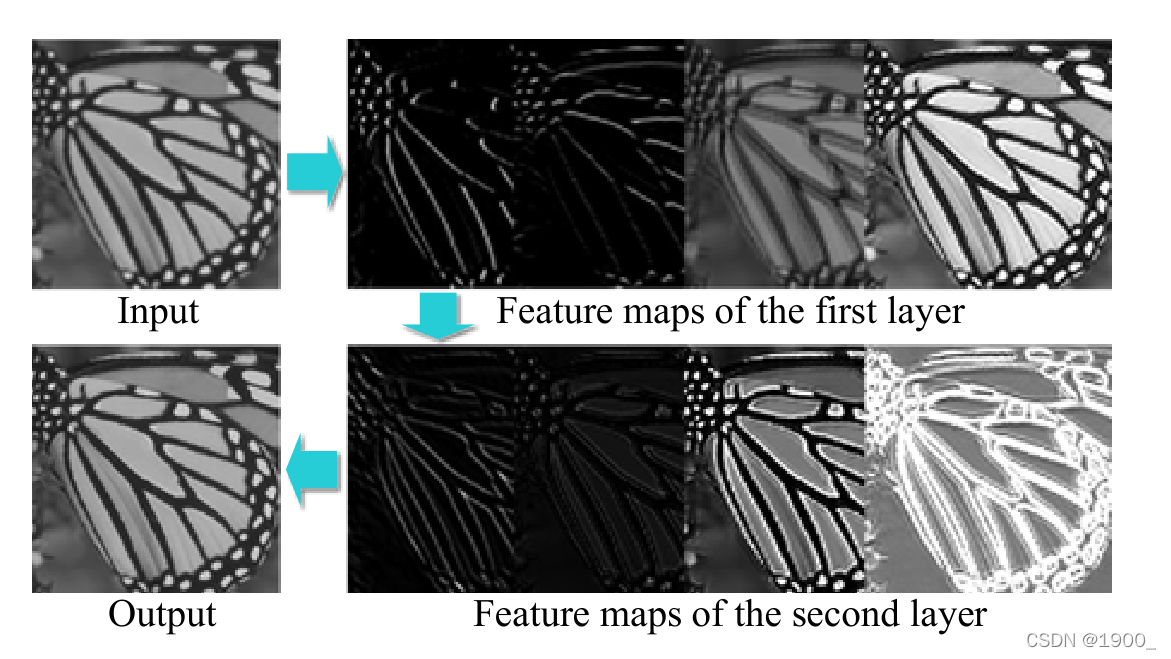
4.3 Model and Performance Trade-Offs（权衡）

根据基本的网络设置（即$f_1=9，f_2=1，f_3=5，n_1=64，n_2=32$），我们将逐步修改其中一些参数，以研究性能与速度之间的最佳权衡 ，并研究性能和参数之间的关系。

4.3.1 Filter Number

根据我们的网络默认设置n1=64和n2=32，我们进行了两个实验：
（i）一个是使用n1=128且n2=64的较大网络，以及（ii）另一个 在n1=32和n2 =16的较小网络中。

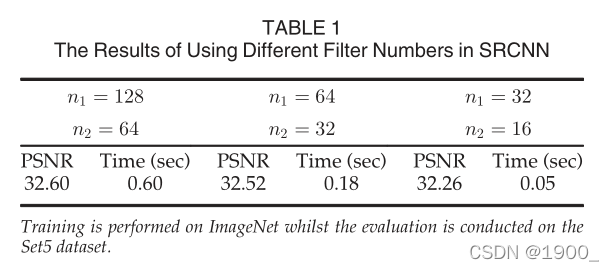
实验结果表明。可以通过增加网络宽度（增加过滤器数量）来实现卓越的性能。但是，如果想要恢复速度快，最好选择较小的网络宽度，这仍然比基于稀疏编码的方法(31.42 dB)有更好的性能。

4.3.2 Filter Size

在本节中，我们研究了网络对不同过滤器大小的敏感性。 在先前的实验中，我们将过滤器大小设置为f1=9，f2=1和f3=5，并且网络可以表示为9-1-5。 首先，为了与基于稀疏编码的方法保持一致，我们将第二层的过滤器大小固定为f2=1，并将其他层的过滤器大小扩大到f1=11和f3=7（11-1-7）。所有其他设置与第4.1节相同。Set5的放大系数为3的结果为32.57 dB，略高于第4.1节中报告的32.52 dB。这表明，较大的过滤器尺寸可以捕获更丰富的结构信息，从而获得更好的结果。
不同过滤器尺寸的实验结果：

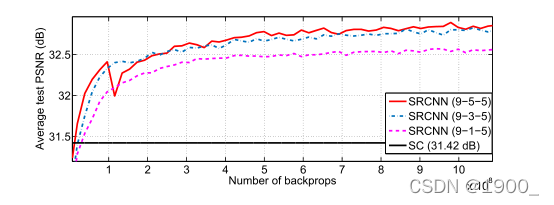
但是，随着过滤器尺寸的增大，部署速度也会降低。 例如，参数9-1-5、9-3-5和9-5-5的数量分别为8,032、24,416和57,184。 9-5-5的复杂度几乎是9-3-5的两倍，但是性能提升是微不足道的。 因此，网络规模的选择应始终在性能和速度之间进行权衡。

4.3.3 Number of Layers

最新研究表明，适度增加网络深度可以使CNN受益。
在这里，我们通过添加另一个滤波器$n_{22}=16$，尺寸大小为$f_{22}=1$的非线性映射层来尝试更深的结构。我们进行了三个控制实验，即9-1-1-5、9-3-1 -5、9-5-1-5，分别在9-1-5、9-3-5和9-5-5上添加一个附加层。 附加层的初始化方案和学习率与第二层相同。实验结果如下图：

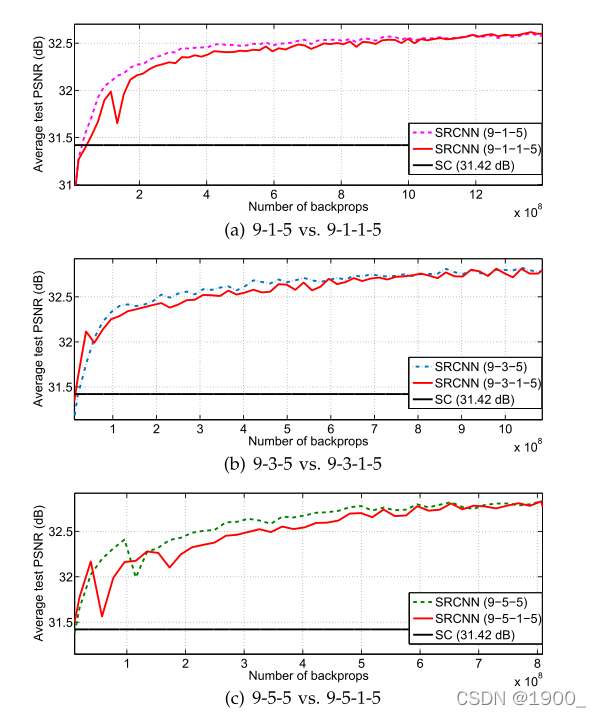
我们发现更深的网络并不一定总能带来更好的性能。如下图：

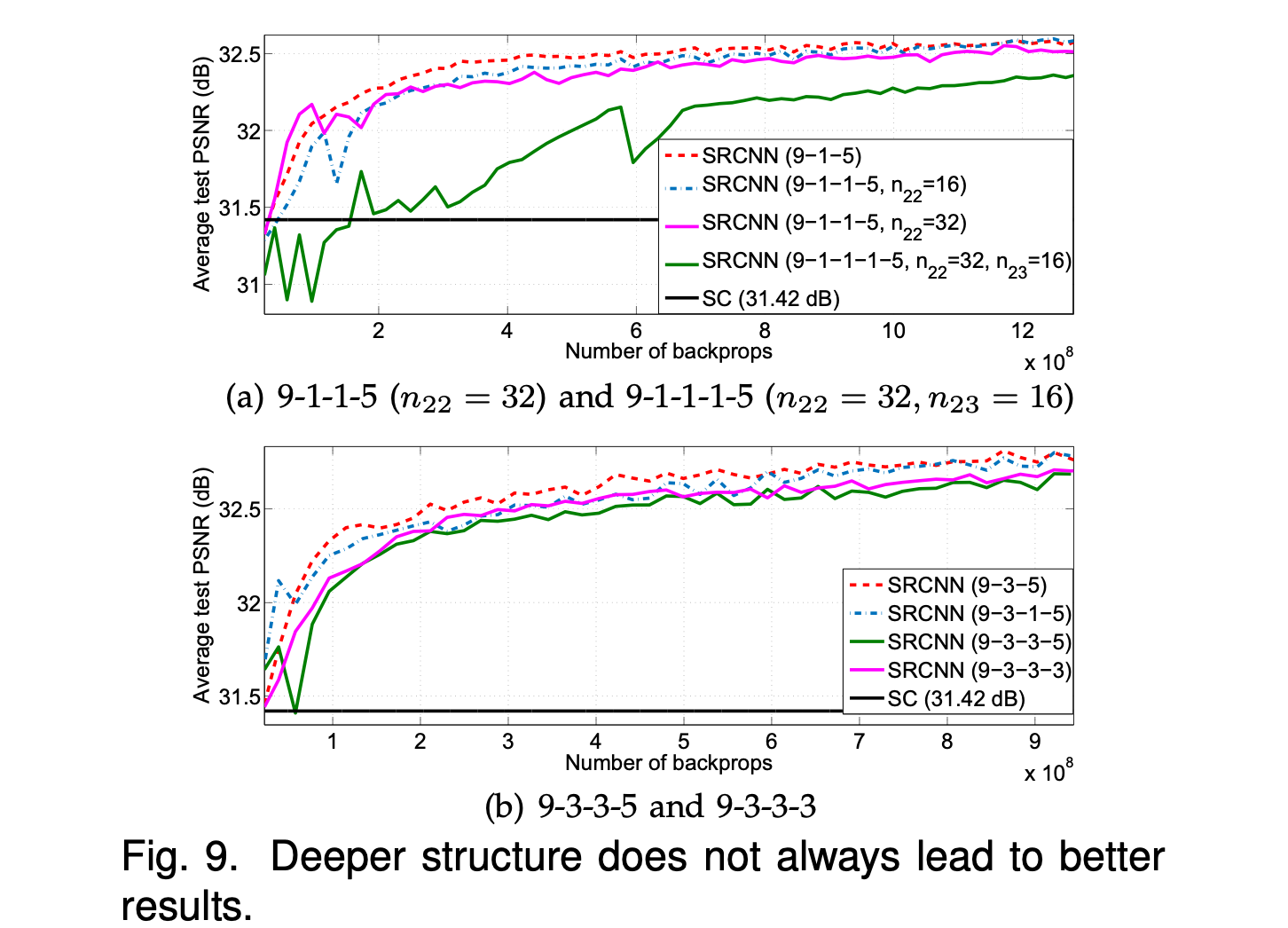
所有这些实验表明，在这种超分辨率的深层模型中，并不是“越深越好”。 这可能是由于训练困难造成的。 我们的CNN网络不包含池化层或全连接层，因此它对初始化参数和学习率敏感。 当我们深入学习时（例如4或5层），我们很难设置合适的学习速率来保证收敛。 即使收敛，网络也可能会陷入不良的局部最小值，并且即使有足够的训练时间，学习到的滤波器的多样性也会降低。

4.4 Comparisons to State-of-the-Arts

在本节中，我们将我们的方法和最先进方法进行定量与定性地对比。我们采用具有良好性能与速度之间折衷的模型：在ImageNet上训练的f1=9，f2=5，f3=5，n1=64和n2=32的三层网络。对于不同的放大因子{2, 3, 4}，我们为这个因素训练了一个特定的网络。与下面这几个最新的方法比较：

除了广泛使用的PSNR和SSIM指数[43]，我们还采用了另外四个评估矩阵，即信息保真度标准（IFC），噪声质量度量（NQM），加权峰值信噪比 （WPSNR）和多尺度结构相似性指数（MSSSIM）。

4.4.1 Quantitative and Qualitative Evaluation

如表2、3和4所示，在所有实验中，提出的SRCNN在大多数评估矩阵中得分最高（可以在补充文件中找到每个图像的PSNR值。）

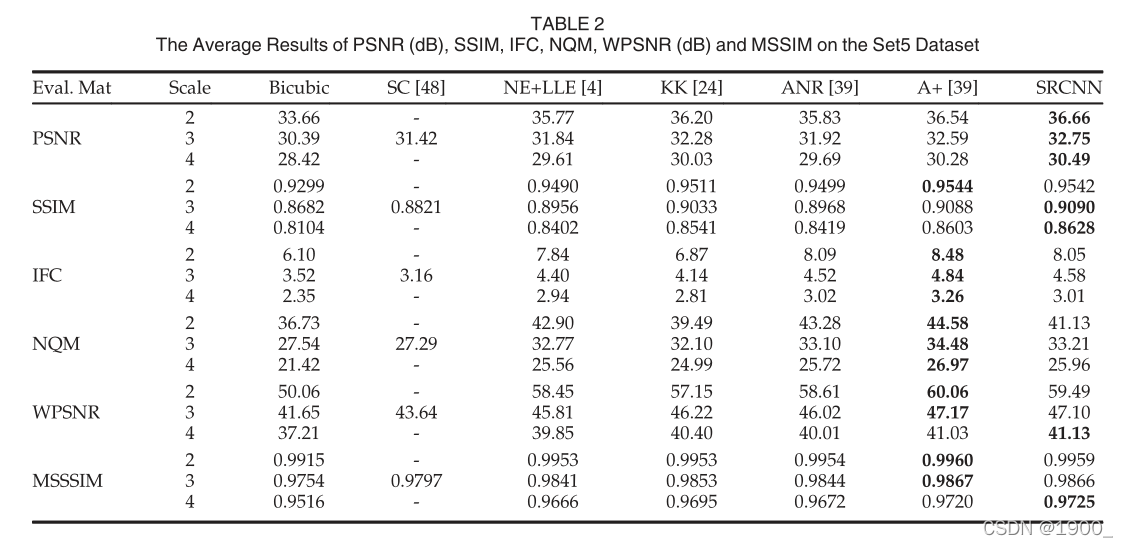
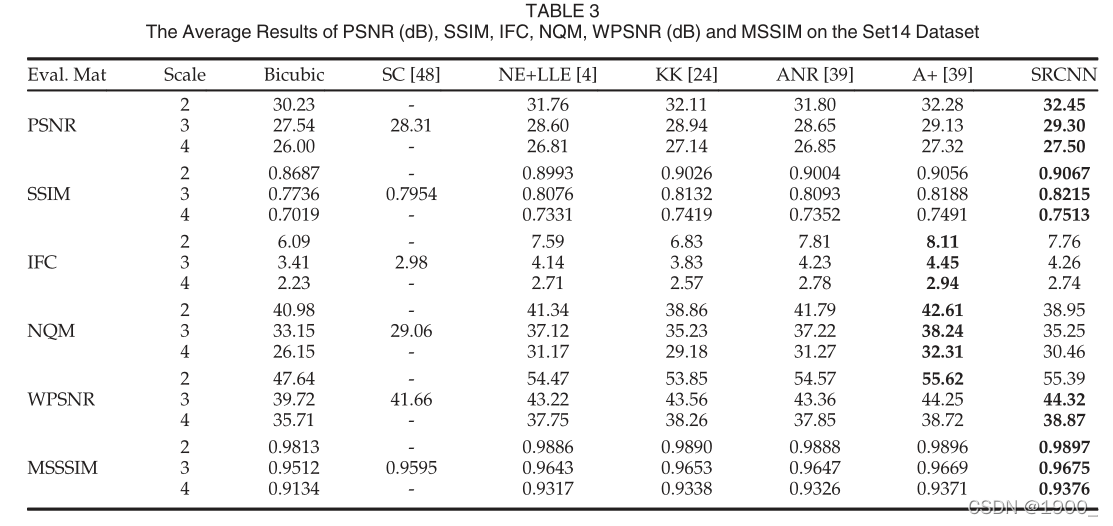
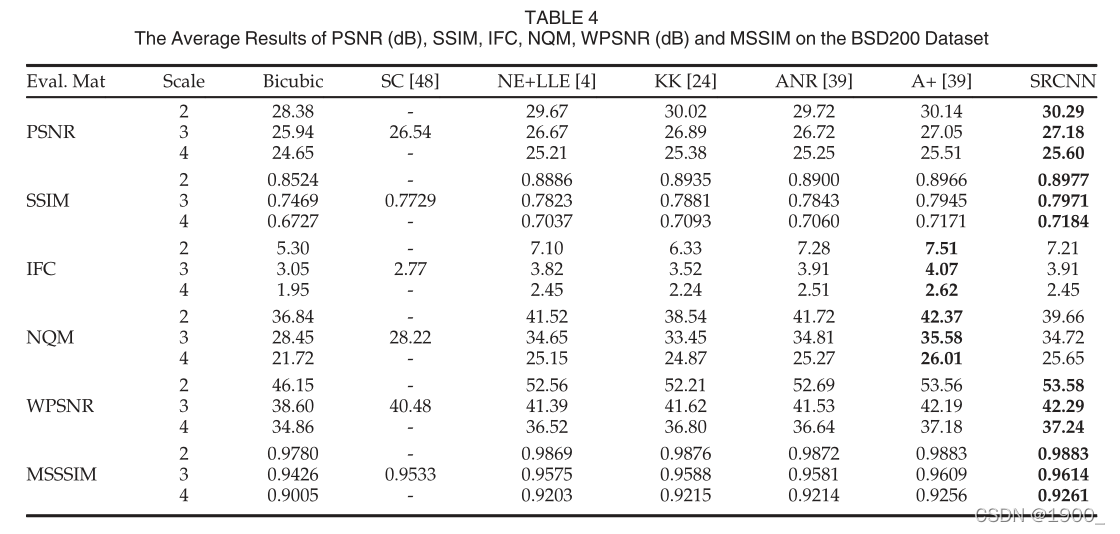
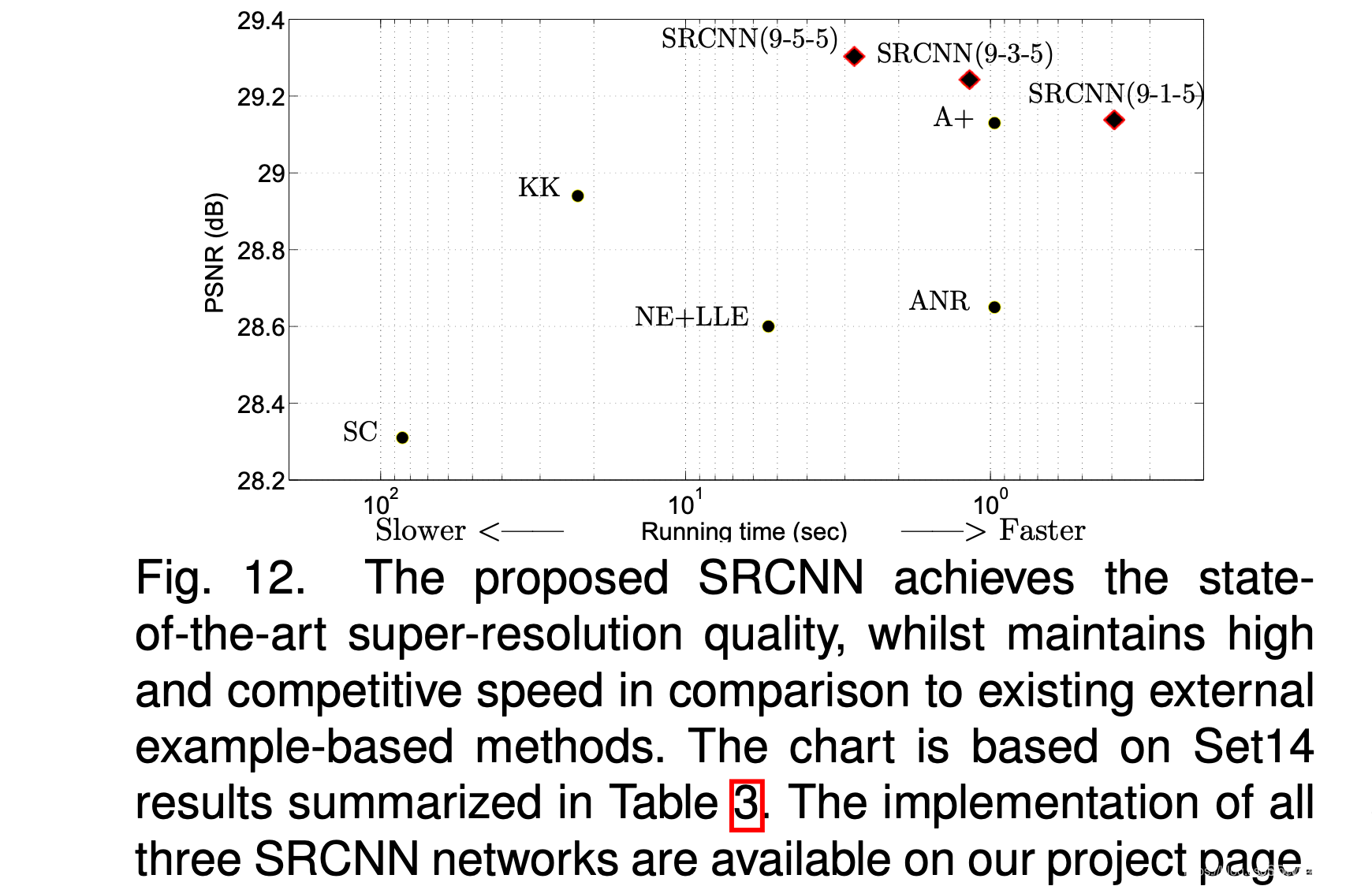
4.4.2 Running Time

图12为几种最先进方法的运行时间比较，以及它们在Set14上的恢复性能。

4.5 Experiments on Color Channels

探索了彩色图像超分辨率的不同训练策略，随后评估了它们在不同通道上的性能。

5 CONCLUSION

我们提出了一种用于单图像超分辨率（SR）的新颖的深度学习方法。 我们表明，传统的基于稀疏编码的SR方法可以重新构造为深度卷积神经网络。 所提出的方法SRCNN，学习了低分辨率和高分辨率图像之间的端到端映射，除了优化之外几乎没有额外的前/后处理。 SRCNN具有轻巧的结构，其性能优于最先进的方法。 我们推测，通过探索更多的过滤条件和不同的训练策略，可以进一步获得额外的表现。 此外，所提出的结构具有简单性和鲁棒性的优点，可以应用于其他低级视觉问题，例如图像去模糊或同时进行SR +去噪。 人们还可以研究一种网络来应对不同的提升因素。