引言
在《决策树学习(上)——深度原理剖析及源码实现》中,我们讨论了决策树的基本原理、所需要掌握的信息论知识,并在文章的最后给出了Java源码实现。在这一节,我们继续讨论基于决策树学习的算法。由于基于决策树的算法比较多且受篇幅限制,本文我们只讨论著名的ID3、C4.5以及CART算法,并在文章最后给出源码实现。
ID3与C4.5
ID3(Iterative Dichotomiser 3,迭代二叉树3代)由Ross Quinlan于1986年提出。1993年,他对ID3进行改进设计出了C4.5算法。值得称道的是,Quinlan在1998年提出了基于C4.5改进的C5.0算法。
在《决策树学习(上)——深度原理剖析及源码实现》中(下文简称《上》),我们已经知道ID3与C4.5的不同之处在于,ID3根据信息增益选取特征构造决策树,而C4.5则是以信息增益率为核心构造决策树,这两种方式的计算法方法在《上》中已经给出。既然C4.5是在ID3的基础上改进得到的,那么这两者的优缺点分别是什么?
剖析ID3与C4.5优缺点
在《上》中我们已经讨论过,使用信息增益会让ID3算法更偏向于选择值多的属性。信息增益反映给定一个条件后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是信息熵越小,信息增益越大。因此,在一定条件下,值多的属性具有更大的信息增益。而C4.5则使用信息增益率选择属性。信息增益率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的属性,分裂信息用来衡量属性分裂数据的广度和均匀性。这样就改进了ID3偏向选择值多属性的缺点。
此外,通过学术界及工业界的研究ID3还具有如下缺点:
- ID3是单变量决策树(在分枝节点上只考虑单个属性),许多复杂概念的表达困难,属性相互关系强调不够,容易导致决策树中子树的重复或有些属性在决策树的某一路径上被检验多次。
- 抗噪性差,训练例子中正例和反例的比例较难控制。
- ID3是非递增算法。
- 只能处理离散数据。
考虑到ID3的上述缺点,Quinlan对其进行改进的到C4.5。C4.5除了前面谈到的使用信息增益率而避免了选择值多的属性的优点之外,相比于ID3还有如下优点:
相对于ID3只能处理离散数据,C4.5还能对连续属性进行处理,具体步骤为:
- 把需要处理的样本(对应根节点)或样本子集(对应子树)按照连续变量的大小从小到大进行排序。
- 假设该属性对应的不同的属性值一共有N个,那么总共有N−1个可能的候选分割阈值点,每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点,根据这个分割点把原来连续的属性分成bool属性。实际上可以不用检查所有N−1个分割点。(连续属性值比较多的时候,由于需要排序和扫描,会使C4.5的性能有所下降。)
- 用信息增益比率选择最佳划分。
C4.5算法能够处理不完整的数据,常用的处理方法有以下三种:
- 给缺失属性赋予最常见的值。
- 丢弃含有缺失值的样本。
- 根据节点的样例上该属性值出现的情况赋一个概率值。
在决策树构造的过程中进行剪枝,从而可以在一定程度上避免过拟合(Overfitting)
- 建议在构造树的过程中不考虑拥有几个元素的节点。
从上面的讨论可以总结出,C4.5产生的分类规则易于理解,准确率较高。但由于在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法会牺牲一定的效率。另外,无论是ID3还是C4.5最好在小数据集上使用,决策树分类一般适用于小数据。当属性取值很多时最好选择C4.5算法,ID3得出的效果会比较差。
ID3源码实现(C++版本)
感谢Coding for Dreams的源码贡献
训练数据集如下:
Day Outlook Temperature Humidity Wind PlayTennis
1 Sunny Hot High Weak no
2 Sunny Hot High Strong no
3 Overcast Hot High Weak yes
4 Rainy Mild High Weak yes
5 Rainy Cool Normal Weak yes
6 Rainy Cool Normal Strong no
7 Overcast Cool Normal Strong yes
8 Sunny Mild High Weak no
9 Sunny Cool Normal Weak yes
10 Rainy Mild Normal Weak yes
11 Sunny Mild Normal Strong yes
12 Overcast Mild High Strong yes
13 Overcast Hot Normal Weak yes
14 Rainy Mild High Strong no
end
源码如下:
#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <algorithm>
#include <cmath>
using namespace std;
#define MAXLEN 6//输入每行的数据个数
//多叉树的实现
//1 广义表
//2 父指针表示法,适于经常找父结点的应用
//3 子女链表示法,适于经常找子结点的应用
//4 左长子,右兄弟表示法,实现比较麻烦
//5 每个结点的所有孩子用vector保存
//教训:数据结构的设计很重要,本算法采用5比较合适,同时
//注意维护剩余样例和剩余属性信息,建树时横向遍历考循环属性的值,
//纵向遍历靠递归调用
vector <vector <string> > state;//实例集
vector <string> item(MAXLEN);//对应一行实例集
vector <string> attribute_row;//保存首行即属性行数据
string end("end");//输入结束
string yes("yes");
string no("no");
string blank("");
map<string,vector < string > > map_attribute_values;//存储属性对应的所有的值
int tree_size = 0;
struct Node{//决策树节点
string attribute;//属性值
string arrived_value;//到达的属性值
vector<Node *> childs;//所有的孩子
Node(){
attribute = blank;
arrived_value = blank;
}
};
Node * root;
//根据数据实例计算属性与值组成的map
void ComputeMapFrom2DVector(){
unsigned int i,j,k;
bool exited = false;
vector<string> values;
for(i = 1; i < MAXLEN-1; i++){//按照列遍历
for (j = 1; j < state.size(); j++){
for (k = 0; k < values.size(); k++){
if(!values[k].compare(state[j][i])) exited = true;
}
if(!exited){
values.push_back(state[j][i]);//注意Vector的插入都是从前面插入的,注意更新it,始终指向vector头
}
exited = false;
}
map_attribute_values[state[0][i]] = values;
values.erase(values.begin(), values.end());
}
}
//根据具体属性和值来计算熵
double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){
vector<int> count (2,0);
unsigned int i,j;
bool done_flag = false;//哨兵值
for(j = 1; j < MAXLEN; j++){
if(done_flag) break;
if(!attribute_row[j].compare(attribute)){
for(i = 1; i < remain_state.size(); i++){
if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算父节点
if(!remain_state[i][MAXLEN - 1].compare(yes)){
count[0]++;
}
else count[1]++;
}
}
done_flag = true;
}
}
if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例
//具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数
double sum = count[0] + count[1];
double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);
return entropy;
}
//计算按照属性attribute划分当前剩余实例的信息增益
double ComputeGain(vector <vector <string> > remain_state, string attribute){
unsigned int j,k,m;
//首先求不做划分时的熵
double parent_entropy = ComputeEntropy(remain_state, attribute, blank, true);
double children_entropy = 0;
//然后求做划分后各个值的熵
vector<string> values = map_attribute_values[attribute];
vector<double> ratio;
vector<int> count_values;
int tempint;
for(m = 0; m < values.size(); m++){
tempint = 0;
for(k = 1; k < MAXLEN - 1; k++){
if(!attribute_row[k].compare(attribute)){
for(j = 1; j < remain_state.size(); j++){
if(!remain_state[j][k].compare(values[m])){
tempint++;
}
}
}
}
count_values.push_back(tempint);
}
for(j = 0; j < values.size(); j++){
ratio.push_back((double)count_values[j] / (double)(remain_state.size()-1));
}
double temp_entropy;
for(j = 0; j < values.size(); j++){
temp_entropy = ComputeEntropy(remain_state, attribute, values[j], false);
children_entropy += ratio[j] * temp_entropy;
}
return (parent_entropy - children_entropy);
}
int FindAttriNumByName(string attri){
for(int i = 0; i < MAXLEN; i++){
if(!state[0][i].compare(attri)) return i;
}
cerr<<"can't find the numth of attribute"<<endl;
return 0;
}
//找出样例中占多数的正/负性
string MostCommonLabel(vector <vector <string> > remain_state){
int p = 0, n = 0;
for(unsigned i = 0; i < remain_state.size(); i++){
if(!remain_state[i][MAXLEN-1].compare(yes)) p++;
else n++;
}
if(p >= n) return yes;
else return no;
}
//判断样例是否正负性都为label
bool AllTheSameLabel(vector <vector <string> > remain_state, string label){
int count = 0;
for(unsigned int i = 0; i < remain_state.size(); i++){
if(!remain_state[i][MAXLEN-1].compare(label)) count++;
}
if(count == remain_state.size()-1) return true;
else return false;
}
//计算信息增益,DFS构建决策树
//current_node为当前的节点
//remain_state为剩余待分类的样例
//remian_attribute为剩余还没有考虑的属性
//返回根结点指针
Node * BulidDecisionTreeDFS(Node * p, vector <vector <string> > remain_state, vector <string> remain_attribute){
//if(remain_state.size() > 0){
//printv(remain_state);
//}
if (p == NULL)
p = new Node();
//先看搜索到树叶的情况
if (AllTheSameLabel(remain_state, yes)){
p->attribute = yes;
return p;
}
if (AllTheSameLabel(remain_state, no)){
p->attribute = no;
return p;
}
if(remain_attribute.size() == 0){//所有的属性均已经考虑完了,还没有分尽
string label = MostCommonLabel(remain_state);
p->attribute = label;
return p;
}
double max_gain = 0, temp_gain;
vector <string>::iterator max_it = remain_attribute.begin();
vector <string>::iterator it1;
for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++){
temp_gain = ComputeGain(remain_state, (*it1));
if(temp_gain > max_gain) {
max_gain = temp_gain;
max_it = it1;
}
}
//下面根据max_it指向的属性来划分当前样例,更新样例集和属性集
vector <string> new_attribute;
vector <vector <string> > new_state;
for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++){
if((*it2).compare(*max_it)) new_attribute.push_back(*it2);
}
//确定了最佳划分属性,注意保存
p->attribute = *max_it;
vector <string> values = map_attribute_values[*max_it];
int attribue_num = FindAttriNumByName(*max_it);
new_state.push_back(attribute_row);
for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++){
for(unsigned int i = 1; i < remain_state.size(); i++){
if(!remain_state[i][attribue_num].compare(*it3)){
new_state.push_back(remain_state[i]);
}
}
Node * new_node = new Node();
new_node->arrived_value = *it3;
if(new_state.size() == 0){//表示当前没有这个分支的样例,当前的new_node为叶子节点
new_node->attribute = MostCommonLabel(remain_state);
}
else
BulidDecisionTreeDFS(new_node, new_state, new_attribute);
//递归函数返回时即回溯时需要1 将新结点加入父节点孩子容器 2清除new_state容器
p->childs.push_back(new_node);
new_state.erase(new_state.begin()+1,new_state.end());//注意先清空new_state中的前一个取值的样例,准备遍历下一个取值样例
}
return p;
}
void Input(){
string s;
while(cin>>s,s.compare(end) != 0){//-1为输入结束
item[0] = s;
for(int i = 1;i < MAXLEN; i++){
cin>>item[i];
}
state.push_back(item);//注意首行信息也输入进去,即属性
}
for(int j = 0; j < MAXLEN; j++){
attribute_row.push_back(state[0][j]);
}
}
void PrintTree(Node *p, int depth){
for (int i = 0; i < depth; i++) cout << '\t';//按照树的深度先输出tab
if(!p->arrived_value.empty()){
cout<<p->arrived_value<<endl;
for (int i = 0; i < depth+1; i++) cout << '\t';//按照树的深度先输出tab
}
cout<<p->attribute<<endl;
for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){
PrintTree(*it, depth + 1);
}
}
void FreeTree(Node *p){
if (p == NULL)
return;
for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){
FreeTree(*it);
}
delete p;
tree_size++;
}
int main(){
Input();
vector <string> remain_attribute;
string outlook("Outlook");
string Temperature("Temperature");
string Humidity("Humidity");
string Wind("Wind");
remain_attribute.push_back(outlook);
remain_attribute.push_back(Temperature);
remain_attribute.push_back(Humidity);
remain_attribute.push_back(Wind);
vector <vector <string> > remain_state;
for(unsigned int i = 0; i < state.size(); i++){
remain_state.push_back(state[i]);
}
ComputeMapFrom2DVector();
root = BulidDecisionTreeDFS(root,remain_state,remain_attribute);
cout<<"the decision tree is :"<<endl;
PrintTree(root,0);
FreeTree(root);
cout<<endl;
cout<<"tree_size:"<<tree_size<<endl;
return 0;
}C4.5源码实现
C4.5作者Ross Quinlan在其个人网站上给出了源码下载链接,原汁原味当然更好。网站链接点击这里。他的个人网站上还有关于C5.0的内容,建议有兴趣的同学前往阅读。
CART
CART(Classification And Regression Tree,分类回归树)由L.Breiman,J.Friedman,R.Olshen和C.Stone于1984年提出,是一种应用相当广泛的决策树学习方法。值得一提的是,CART和C4.5一同被评为数据挖掘领域十大算法。
CART算法采用一种二分递归分割的技术,将当前的样本集分为两个子样本集,使得生成的的每个非叶子节点都有两个分支。因此,CART算法生成的决策树是结构简洁的二叉树。
1.分类树
作为一种决策树学习算法,CART与ID3以及C4.5不同,它使用基尼系数(Gini coefficien)对属性进行选则。在《上》中我们曾提及基尼系数的计算公式:
假设我们拥有如下表1所示的动物分类信息表: 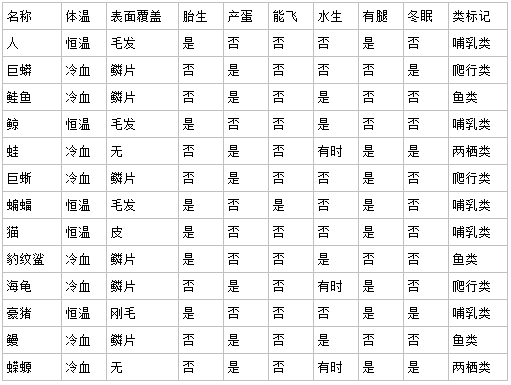
那么对于非恒温动物,包含爬行类3个、鱼类3个、两栖类2个,因此,
Gini1=1-[(3/8)^2 + (3/8)^2 +(2/8)^2 ]
而对于恒温动物,只包含5个哺乳类,同样,
Gini2=1 - 1^2 = 0
同熵一样,如果样本集合D被某个属性A是否取某个值分成两个样本集合D1和D2,则在属性A的条件下,集合D的基尼指数定义为: 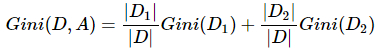
对于上述按恒温和非恒温属性划分动物,
Gini(D, A)= 8/13 * Gini1 + 5/13 * Gini2
在一定程度上基尼指数(Gini(D))反应的是集合D的不确定程度,跟熵类似。Gini(D, A)反应的是经过特征A划分后集合D的不确定程度。基尼系数越大,样本集合的不确定性也就越大。因此最好的属性划分是使得Gini(D, A)最小的划分。
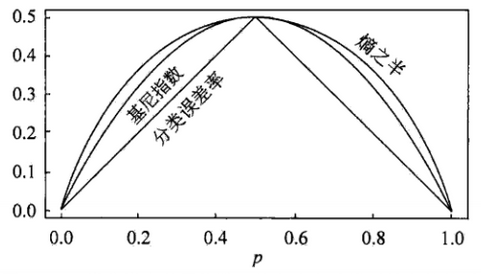
下图显示了二分类问题中基尼系数、熵(单位比特)之半1/2*H(p)和分类误差率的关系。横坐标表示概率p,纵坐标表示损失。可以看出基尼系数和熵之半曲线很接近,都可以近似的代表分类误差率。
CART的生成过程与《上》中决策树生成过程类似,每一次选择使基尼系数最小的属性作为切分点直到满足停止条件为止。算法的停止条件是节点中的样本个数小于预定阈值,或者样本集的基尼系数小于预定阈值(样本基本属于同一类),或者没有更多特征。
2.回归树
除了分类决策之外,CART也可以进行回归决策。
假设X和Y分别为输入和输出变量,Y为连续变量,训练数据集D为:
一个回归树对应着输入空间的一个划分以及在划分的单元上的输出值。假设已经将输入空间划分为M个单元R1,R2,…,RM,在每个单元Rm上有个固定的输出Cm,则回归树表示为:
问题是怎么对输入空间进行划分。一般采用启发式的思路,选择第 j 个Feature Xj和他的取值s分别作为切分变量(splitting variable)和切分点(splitting point),并定义两个区域:
然后采用平方误差损失求解最优的切分变量j和切分点s。具体地,求解
每一个切分变量和切分点对(j,s)都将输入空间分成两个区域,然后分别求每个区域的输出值,使得误差最小,很显然输出值应该是那个区域所有样本值的平均值,即:
举例说明,下面有一个简单的训练数据,根据这个数据集我们生成一棵回归树。
由于x只有一个Feature,我们不用选择j,下面我们考虑如下的切分点s: 1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5 然后求出对应的R1,R2,c1,c2,以及总的误差:
经过计算,可以得到如下结果:
很显然应该取s=6.5作为切分点,此时:
R1={1,2,3,4,5,6},R2={7,8,9,10},c1=6.24,c2=8.91
决策树为:
然后每个(j,s)对里找出使总误差最小的对作为最终的切分变量和切分点,对切分后的子区域重复这一步骤,直到满足停止条件为止。这样就生成了一颗回归树。此时的回归树成为最小二乘回归树(least squares regression tree)。
3.剪枝
当分类回归树划分得太细时,会对噪声数据产生过拟合作用。因此我们要通过剪枝来解决。决策树剪枝分前剪枝(预剪枝)和后剪枝两种形式。在《上》中曾介绍过, 前剪枝是在构建决策树的过程时,提前停止,这种剪枝一般不能得到很好的效果。而后剪枝首先通过完全分裂构造完整的决策树,允许过拟合,然后采取一定的策略来进行剪枝。常用的后剪枝策略包括:
- 降低错误剪枝 REP(Reduced Error Pruning)
- 悲观错误剪枝 PEP(Pessimistic Error Pruning)
- 基于错误剪枝 EBP(Error Based Pruning)
- 代价复杂度剪枝 CCP(Cost Complexity Pruning)
- 最小错误剪枝 MEP(Minimum Error Pruning)
CART使用的就是后剪枝中的CCP策略。对于CART中的每一个非叶子节点计算它的表面误差率增益值α。
其中,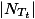
r(t)是节点t的误差率。p(t)是节点t上的数据占所有数据的比例。p(t)是子树Tt的误差代价,如果该节点不被剪枝。它等于子树Tt上所有叶子节点的误差代价之和。我们所需要做的就是找到α值最小的非叶子节点,令其左右孩子为NULL。当多个非叶子节点的α值同时达到最小时,取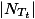
源码实现(C++版)
在这里使用的数据是上述表一中的数据,感谢华夏35度的源码贡献。
#include<iostream>
#include<fstream>
#include<sstream>
#include<string>
#include<map>
#include<list>
#include<set>
#include<queue>
#include<utility>
#include<vector>
#include<cmath>
using namespace std;
//置信水平取0.95时的卡方表
const double CHI[18]={0.004,0.103,0.352,0.711,1.145,1.635,2.167,2.733,3.325,3.94,4.575,5.226,5.892,6.571,7.261,7.962};
/*根据多维数组计算卡方值*/
template<typename Comparable>
double cal_chi(Comparable **arr,int row,int col){
vector<Comparable> rowsum(row);
vector<Comparable> colsum(col);
Comparable totalsum=static_cast<Comparable>(0);
//cout<<"observation"<<endl;
for(int i=0;i<row;++i){
for(int j=0;j<col;++j){
//cout<<arr[i][j]<<"\t";
totalsum+=arr[i][j];
rowsum[i]+=arr[i][j];
colsum[j]+=arr[i][j];
}
//cout<<endl;
}
double rect=0.0;
//cout<<"exception"<<endl;
for(int i=0;i<row;++i){
for(int j=0;j<col;++j){
double excep=1.0*rowsum[i]*colsum[j]/totalsum;
//cout<<excep<<"\t";
if(excep!=0)
rect+=pow(arr[i][j]-excep,2.0)/excep;
}
//cout<<endl;
}
return rect;
}
class MyTriple{
public:
double first;
int second;
int third;
MyTriple(){
first=0.0;
second=0;
third=0;
}
MyTriple(double f,int s,int t):first(f),second(s),third(t){}
bool operator< (const MyTriple &obj) const{
int cmp=this->first-obj.first;
if(cmp>0)
return false;
else if(cmp<0)
return true;
else{
cmp=obj.second-this->second;
if(cmp<0)
return true;
else
return false;
}
}
};
typedef map<string,int> MAP_REST_COUNT;
typedef map<string,MAP_REST_COUNT> MAP_ATTR_REST;
typedef vector<MAP_ATTR_REST> VEC_STATI;
const int ATTR_NUM=8; //自变量的维度
vector<string> X(ATTR_NUM);
int rest_number; //因变量的种类数,即类别数
vector<pair<string,int> > classes; //把类别、对应的记录数存放在一个数组中
int total_record_number; //总的记录数
vector<vector<string> > inputData; //原始输入数据
class node{
public:
node* parent; //父节点
node* leftchild; //左孩子节点
node* rightchild; //右孩子节点
string cond; //分枝条件
string decision; //在该节点上作出的类别判定
double precision; //判定的正确率
int record_number; //该节点上涵盖的记录个数
int size; //子树包含的叶子节点的数目
int index; //层次遍历树,给节点标上序号
double alpha; //表面误差率的增加量
node(){
parent=NULL;
leftchild=NULL;
rightchild=NULL;
precision=0.0;
record_number=0;
size=1;
index=0;
alpha=1.0;
}
node(node* p){
parent=p;
leftchild=NULL;
rightchild=NULL;
precision=0.0;
record_number=0;
size=1;
index=0;
alpha=1.0;
}
node(node* p,string c,string d):cond(c),decision(d){
parent=p;
leftchild=NULL;
rightchild=NULL;
precision=0.0;
record_number=0;
size=1;
index=0;
alpha=1.0;
}
void printInfo(){
cout<<"index:"<<index<<"\tdecisoin:"<<decision<<"\tprecision:"<<precision<<"\tcondition:"<<cond<<"\tsize:"<<size;
if(parent!=NULL)
cout<<"\tparent index:"<<parent->index;
if(leftchild!=NULL)
cout<<"\tleftchild:"<<leftchild->index<<"\trightchild:"<<rightchild->index;
cout<<endl;
}
void printTree(){
printInfo();
if(leftchild!=NULL)
leftchild->printTree();
if(rightchild!=NULL)
rightchild->printTree();
}
};
int readInput(string filename){
ifstream ifs(filename.c_str());
if(!ifs){
cerr<<"open inputfile failed!"<<endl;
return -1;
}
map<string,int> catg;
string line;
getline(ifs,line);
string item;
istringstream strstm(line);
strstm>>item;
for(int i=0;i<X.size();++i){
strstm>>item;
X[i]=item;
}
while(getline(ifs,line)){
vector<string> conts(ATTR_NUM+2);
istringstream strstm(line);
//strstm.str(line);
for(int i=0;i<conts.size();++i){
strstm>>item;
conts[i]=item;
if(i==conts.size()-1)
catg[item]++;
}
inputData.push_back(conts);
}
total_record_number=inputData.size();
ifs.close();
map<string,int>::const_iterator itr=catg.begin();
while(itr!=catg.end()){
classes.push_back(make_pair(itr->first,itr->second));
itr++;
}
rest_number=classes.size();
return 0;
}
/*根据inputData作出一个统计stati*/
void statistic(vector<vector<string> > &inputData,VEC_STATI &stati){
for(int i=1;i<ATTR_NUM+1;++i){
MAP_ATTR_REST attr_rest;
for(int j=0;j<inputData.size();++j){
string attr_value=inputData[j][i];
string rest=inputData[j][ATTR_NUM+1];
MAP_ATTR_REST::iterator itr=attr_rest.find(attr_value);
if(itr==attr_rest.end()){
MAP_REST_COUNT rest_count;
rest_count[rest]=1;
attr_rest[attr_value]=rest_count;
}
else{
MAP_REST_COUNT::iterator iter=(itr->second).find(rest);
if(iter==(itr->second).end()){
(itr->second).insert(make_pair(rest,1));
}
else{
iter->second+=1;
}
}
}
stati.push_back(attr_rest);
}
}
/*依据某条件作出分枝时,inputData被分成两部分*/
void splitInput(vector<vector<string> > &inputData,int fitIndex,string cond,vector<vector<string> > &LinputData,vector<vector<string> > &RinputData){
for(int i=0;i<inputData.size();++i){
if(inputData[i][fitIndex+1]==cond)
LinputData.push_back(inputData[i]);
else
RinputData.push_back(inputData[i]);
}
}
void printStati(VEC_STATI &stati){
for(int i=0;i<stati.size();i++){
MAP_ATTR_REST::const_iterator itr=stati[i].begin();
while(itr!=stati[i].end()){
cout<<itr->first;
MAP_REST_COUNT::const_iterator iter=(itr->second).begin();
while(iter!=(itr->second).end()){
cout<<"\t"<<iter->first<<"\t"<<iter->second;
iter++;
}
itr++;
cout<<endl;
}
cout<<endl;
}
}
void split(node *root,vector<vector<string> > &inputData,vector<pair<string,int> > classes){
//root->printInfo();
root->record_number=inputData.size();
VEC_STATI stati;
statistic(inputData,stati);
//printStati(stati);
//for(int i=0;i<rest_number;i++)
// cout<<classes[i].first<<"\t"<<classes[i].second<<"\t";
//cout<<endl;
/*找到最大化GINI指标的划分*/
double minGain=1.0; //最小的GINI增益
int fitIndex=-1;
string fitCond;
vector<pair<string,int> > fitleftclasses;
vector<pair<string,int> > fitrightclasses;
int fitleftnumber;
int fitrightnumber;
for(int i=0;i<stati.size();++i){ //扫描每一个自变量
MAP_ATTR_REST::const_iterator itr=stati[i].begin();
while(itr!=stati[i].end()){ //扫描自变量上的每一个取值
string condition=itr->first; //判定的条件,即到达左孩子的条件
//cout<<"cond 为"<<X[i]+condition<<"时:";
vector<pair<string,int> > leftclasses(classes); //左孩子节点上类别、及对应的数目
vector<pair<string,int> > rightclasses(classes); //右孩子节点上类别、及对应的数目
int leftnumber=0; //左孩子节点上包含的类别数目
int rightnumber=0; //右孩子节点上包含的类别数目
for(int j=0;j<leftclasses.size();++j){ //更新类别对应的数目
string rest=leftclasses[j].first;
MAP_REST_COUNT::const_iterator iter2;
iter2=(itr->second).find(rest);
if(iter2==(itr->second).end()){ //没找到
leftclasses[j].second=0;
rightnumber+=rightclasses[j].second;
}
else{ //找到
leftclasses[j].second=iter2->second;
leftnumber+=leftclasses[j].second;
rightclasses[j].second-=(iter2->second);
rightnumber+=rightclasses[j].second;
}
}
/**if(leftnumber==0 || rightnumber==0){
cout<<"左右有一边为空"<<endl;
for(int k=0;k<rest_number;k++)
cout<<leftclasses[k].first<<"\t"<<leftclasses[k].second<<"\t";
cout<<endl;
for(int k=0;k<rest_number;k++)
cout<<rightclasses[k].first<<"\t"<<rightclasses[k].second<<"\t";
cout<<endl;
}**/
double gain1=1.0; //计算GINI增益
double gain2=1.0;
if(leftnumber==0)
gain1=0.0;
else
for(int j=0;j<leftclasses.size();++j)
gain1-=pow(1.0*leftclasses[j].second/leftnumber,2.0);
if(rightnumber==0)
gain2=0.0;
else
for(int j=0;j<rightclasses.size();++j)
gain2-=pow(1.0*rightclasses[j].second/rightnumber,2.0);
double gain=1.0*leftnumber/(leftnumber+rightnumber)*gain1+1.0*rightnumber/(leftnumber+rightnumber)*gain2;
//cout<<"GINI增益:"<<gain<<endl;
if(gain<minGain){
//cout<<"GINI增益:"<<gain<<"\t"<<i<<"\t"<<condition<<endl;
fitIndex=i;
fitCond=condition;
fitleftclasses=leftclasses;
fitrightclasses=rightclasses;
fitleftnumber=leftnumber;
fitrightnumber=rightnumber;
minGain=gain;
}
itr++;
}
}
/*计算卡方值,看有没有必要进行分裂*/
//cout<<"按"<<X[fitIndex]+fitCond<<"划分,计算卡方"<<endl;
int **arr=new int*[2];
for(int i=0;i<2;i++)
arr[i]=new int[rest_number];
for(int i=0;i<rest_number;i++){
arr[0][i]=fitleftclasses[i].second;
arr[1][i]=fitrightclasses[i].second;
}
double chi=cal_chi(arr,2,rest_number);
//cout<<"chi="<<chi<<" CHI="<<CHI[rest_number-2]<<endl;
if(chi<CHI[rest_number-2]){ //独立,没必要再分裂了
delete []arr[0]; delete []arr[1]; delete []arr;
return; //不需要分裂函数就返回
}
delete []arr[0]; delete []arr[1]; delete []arr;
/*分裂*/
root->cond=X[fitIndex]+"="+fitCond; //root的分枝条件
//cout<<"分类条件:"<<root->cond<<endl;
node *travel=root; //root及其祖先节点的size都要加1
while(travel!=NULL){
(travel->size)++;
travel=travel->parent;
}
node *LChild=new node(root); //创建左右孩子
node *RChild=new node(root);
root->leftchild=LChild;
root->rightchild=RChild;
int maxLcount=0;
int maxRcount=0;
string Ldicision,Rdicision;
for(int i=0;i<rest_number;++i){ //统计哪种类别出现的最多,从而作出类别判定
if(fitleftclasses[i].second>maxLcount){
maxLcount=fitleftclasses[i].second;
Ldicision=fitleftclasses[i].first;
}
if(fitrightclasses[i].second>maxRcount){
maxRcount=fitrightclasses[i].second;
Rdicision=fitrightclasses[i].first;
}
}
LChild->decision=Ldicision;
RChild->decision=Rdicision;
LChild->precision=1.0*maxLcount/fitleftnumber;
RChild->precision=1.0*maxRcount/fitrightnumber;
/*递归对左右孩子进行分裂*/
vector<vector<string> > LinputData,RinputData;
splitInput(inputData,fitIndex,fitCond,LinputData,RinputData);
//cout<<"左边inputData行数:"<<LinputData.size()<<endl;
//cout<<"右边inputData行数:"<<RinputData.size()<<endl;
split(LChild,LinputData,fitleftclasses);
split(RChild,RinputData,fitrightclasses);
}
/*计算子树的误差代价*/
double calR2(node *root){
if(root->leftchild==NULL)
return (1-root->precision)*root->record_number/total_record_number;
else
return calR2(root->leftchild)+calR2(root->rightchild);
}
/*层次遍历树,给节点标上序号。同时计算alpha*/
void index(node *root,priority_queue<MyTriple> &pq){
int i=1;
queue<node*> que;
que.push(root);
while(!que.empty()){
node* n=que.front();
que.pop();
n->index=i++;
if(n->leftchild!=NULL){
que.push(n->leftchild);
que.push(n->rightchild);
//计算表面误差率的增量
double r1=(1-n->precision)*n->record_number/total_record_number; //节点的误差代价
double r2=calR2(n);
n->alpha=(r1-r2)/(n->size-1);
pq.push(MyTriple(n->alpha,n->size,n->index));
}
}
}
/*剪枝*/
void prune(node *root,priority_queue<MyTriple> &pq){
MyTriple triple=pq.top();
int i=triple.third;
queue<node*> que;
que.push(root);
while(!que.empty()){
node* n=que.front();
que.pop();
if(n->index==i){
cout<<"将要剪掉"<<i<<"的左右子树"<<endl;
n->leftchild=NULL;
n->rightchild=NULL;
int s=n->size-1;
node *trav=n;
while(trav!=NULL){
trav->size-=s;
trav=trav->parent;
}
break;
}
else if(n->leftchild!=NULL){
que.push(n->leftchild);
que.push(n->rightchild);
}
}
}
void test(string filename,node *root){
ifstream ifs(filename.c_str());
if(!ifs){
cerr<<"open inputfile failed!"<<endl;
return;
}
string line;
getline(ifs,line);
string item;
istringstream strstm(line); //跳过第一行
map<string,string> independent; //自变量,即分类的依据
while(getline(ifs,line)){
istringstream strstm(line);
//strstm.str(line);
strstm>>item;
cout<<item<<"\t";
for(int i=0;i<ATTR_NUM;++i){
strstm>>item;
independent[X[i]]=item;
}
node *trav=root;
while(trav!=NULL){
if(trav->leftchild==NULL){
cout<<(trav->decision)<<"\t置信度:"<<(trav->precision)<<endl;;
break;
}
string cond=trav->cond;
string::size_type pos=cond.find("=");
string pre=cond.substr(0,pos);
string post=cond.substr(pos+1);
if(independent[pre]==post)
trav=trav->leftchild;
else
trav=trav->rightchild;
}
}
ifs.close();
}
int main(){
string inputFile="animal";
readInput(inputFile);
VEC_STATI stati; //最原始的统计
statistic(inputData,stati);
// for(int i=0;i<classes.size();++i)
// cout<<classes[i].first<<"\t"<<classes[i].second<<"\t";
// cout<<endl;
node *root=new node();
split(root,inputData,classes); //分裂根节点
priority_queue<MyTriple> pq;
index(root,pq);
root->printTree();
cout<<"剪枝前使用该决策树最多进行"<<root->size-1<<"次条件判断"<<endl;
/**
//检验一个是不是表面误差增量最小的被剪掉了
while(!pq.empty()){
MyTriple triple=pq.top();
pq.pop();
cout<<triple.first<<"\t"<<triple.second<<"\t"<<triple.third<<endl;
}
**/
test(inputFile,root);
prune(root,pq);
cout<<"剪枝后使用该决策树最多进行"<<root->size-1<<"次条件判断"<<endl;
test(inputFile,root);
return 0;
}总结
C4.5算法是在ID3算法的基础上采用信息增益率的方法选择决策属性。 C4.5改进了ID3偏向选择值多属性以及只能处理离散属性等缺点。ID3算法和C4.5算法虽然在对训练样本集的学习中能尽可能多地挖掘信息,但其生成的决策树分支较大,规模较大。为了简化决策树的规模,提高生成决策树的效率,又出现了根据GINI系数来选择测试属性的决策树算法CART。
CART算法采用一种二分递归分割的技术,与基于信息熵的算法不同,CART算法对每次样本集的划分计算GINI系数,GINI系数越小则划分越合理。CART算法总是将当前样本集分割为两个子样本集,使得生成的决策树的每个非叶结点都只有两个分枝。因此CART算法生成的决策树是结构简洁的二叉树。
参考文献及推荐阅读
- 统计学习方法,李航著;
- http://leijun00.github.io/2014/09/decision-tree/
- http://www.cnblogs.com/zhangchaoyang/articles/2709922.html
- http://www.cnblogs.com/zhangchaoyang/articles/2196631.html
- http://blog.csdn.net/yangliuy/article/details/7322015
(by希慕,新浪微博:@希慕_North)











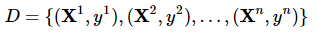
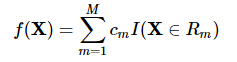

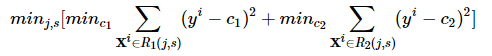
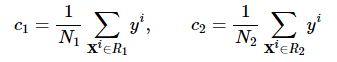

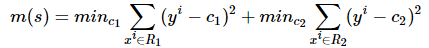

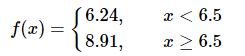

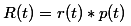













 266
266











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








