K-means 聚类算法及其代码实现

序言

K-means算法是非监督学习（unsupervised learning）中最简单也是最常用的一种聚类算法，具有的特点是:

• 对初始化敏感。初始点选择的不同，可能会产生不同的聚类结果
• 最终会收敛。不管初始点如何选择，最终都会收敛。

本文章介绍K-means聚类算法的思想，同时给出在matlab环境中实现K-means算法的代码。代码使用向量化（vectorization1）来计算，可能不是很直观但是效率比使用循环算法高。

K-means算法

本节首先直观叙述要解决的问题，然后给出所要求解的数学模型，最后从EM2 算法的角度分析K-means算法的特点。

问题描述

首先我们有N个数据 D={x1,x2,...,xN} ，我们想把这些数据分成K个类。首先我们没有任何的 label 信息，所以这是一个unsupervied learning的问题。这个问题有一些难点，在于我们并不知道 K 选择多大时分类是合适的，另外由于这个问题对初始点的选择是敏感的，我们也不好判断怎么样的初始点是好的。所以，我们定义一个距离的概念，这个距离可以是很多种，例如就用最简单的欧式距离 ∥⋅∥ 来作为判断标准，又因为这里对每个点，使用距离或者是距离的平方，其实并没有什么影响，所以为了计算方便，我们就直接使用距离的平方 ∥⋅∥2 作为标准。我们想找到 K 个中心，数据离哪些中心近我们就将其定义为哪一类，同时我们的 K 个中心能够使这个分类最合理也就是每个点到其中心的距离的和最小。用语言描述为

找 K 个中心，数据属于距离其最近的中心一类，这 K 个中心能使所有数据距离其中心的距离和最小。

为了更好的理解，我将在下节给出一些数学符号来定义清楚问题。

问题定义

上小节我们知道要把数据分成 K 个类别，就是要找出 K 个中心点，我们将这些 K 个中心点定义为 {μk}|Kk=1 . 同时，对于数据 D={x1,x2,x3,...,xN} ，我们定义一个类别指示变量（set of binary indicator variables3） {rnk|rnk∈{0,1}} ，表示 xn(n∈(1,2,...,N)) 是否属于第 k 个中心点的类，属于就是1，不属于就是0。因为我们定义数据点属于离他最近的中心点的类，所以 rnk 的计算过程为：

rnk=⎧⎩⎨1,k=argminj||xn−μj||0,otherwise.(1)

我们的目标就是要得到 K 个中心点，能够使每个数据点到其中心点的距离（距离的平方）和最短，也就是让目标函数 

J=∑n=1N∑k=1Krnk||xn−μk||2(2)

最小。

问题求解

这一部分将介绍使用EM算法4来求解K-means问题。关于EM算法求解总体分为两种步骤

• E(expectation): 求期望最大。初始化时，随机生成 K 个中心点 {μk}|Kk=1 。然后使用公式 (1) 决定数据的类别。
• M(Maximization): 这里的极大化取决于你的问题，我们这里是要最优化目标函数。所以在这一步我们保持数据的类别不变，要使用公式 (2) 更新中心点，也就是要求出 
  
  μk=argminukJ(3)
  
  这个等式。 
  这里我们注意到，因为保持了类别不变，也就是说目标函数只有 μk 一个变量，等式 (3) 变成了 
  
  μk=argminukJ(μk)
  
  式子。所以我们对目标函数求极值，也就对 μk 求导并令其为零，得到 
  
  2∑n=1Nrnk(xn−μk)=0
  
  这样的式子。求解可以得到 
  
  μk=∑nrnkxn∑nrnk(4)
  
  的表达式。
• 重复以上两步，直到收敛。

至此，我们就完成了对K-means方法的求解。接下来，我们将通过实例以及代码实现来理解K-means。

K-means实现

这一节主要通过实例和代码，来充分理解K-means算法，完成聚类分析，并在最后分析收敛效果。

实例分析

我们的数据来源是Old Faithful Geyser，我们想将其分成 K 个类。但在处理之前需要对其进行归一化，我对数据进行了标准归一化，数据文件以及源代码都已经放在我的github上面了。

代码分析

都代码还是先整体再局部吧。我们先对代码整体设计如下

function [costDis] = runKMeans(K,fileString)
X=load(fileString);
%determine and store data set information
N=size(X,1);
D=size(X,2);
%allocate space for the K mu vectors
Kmus=zeros(K,D); % not need to allocate it but it is still worthy
%initialize cluster centers by randomly picking points from the data
rndinds=randperm(N);
Kmus=X(rndinds(1:K),:);
%specify the maximum number of iterations to allow
maxiters=1000;
for iter=1:maxiters
    %do this by first calculating a squared distance matrix where the n,k entry
    %contains the squared distance from the nth data vector to the kth mu vector
    %sqDmat will be an N-by-K matrix with the n,k entry as specfied above
    sqDmat=calcSqDistances(X,Kmus);
    %given the matrix of squared distances, determine the closest cluster
    %center for each data vector 
    Rnk=determineRnk(sqDmat);
    KmusOld=Kmus;
    plotCurrent(X,Rnk,Kmus);  
    pause(1);
    Kmus=recalcMus(X,Rnk);
    %check to see if the cluster centers have converged.  If so, break.
    if sum(abs(KmusOld(:)-Kmus(:)))<1e-6
        disp(iter);
        break
    end
end
costDis = sum(min(sqDmat,[],2));
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

首先读入数据，X为 N×D 维的矩阵。然后初始化中心点Kmus 为 K×D 维度的矩阵。接下来进入循环，先使用函数calcSqDistances() 计算数据与各中心点之间的距离，然后determineRnk()根据距离决定数据属于哪一类，然后recalcMus()根据确定好的数据的类重新计算出新的中心点，最后重复循环直到收敛。

接下来是各个内部函数，首先是距离计算函数。我们要得到的矩阵第 n 行第 k 列元素代表的是 ||xn−μk||2 ，也就是

(X(n:,)-Kmus(k:,))*(X(n:,)-Kmus(k:,))'
 
 
1
 
 
1

这样就能够计算出一个元素的值，这里面还要用到一点矩阵运算的技巧，因为

||xn−μk||2=(xn−μk)(xn−μk)T=xnxTn−2xnμTk+μμT(5)

可以发现，其实对数据和中心点矩阵的每一行元素，只要计算自己与自己的距离，然后减去两倍向量乘积的值就可以了。所以我们应该对每个矩阵先自己相乘得到自己的距离，比如对数据点这个距离就通过

Data_sq = diag(X*X');   % N by 1
 
 
1
 
 
1

来计算得出。 
计算距离的代码为

function SQD = calcSqDistances(X,Kmus)
% compute the squared distance w.r.t. each center point for every data
% X; N by D; Kmus: K by D
% ||x-u||^2 = xx' - 2xu' + uu'  N by K
N = size(X,1);
D = size(X,2);
K = size(Kmus,1);
Data_sq = diag(X*X');   % N by 1
Kmus_sq = diag(Kmus*Kmus');    % 1 by K
trans = 2*X*Kmus';  % N by K
SQD = repmat(Data_sq,1,K) - trans + repmat(Kmus_sq',N,1);
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
 
 
1
2
3
4
5
6
7
8
9
10
11
12

决定类的函数，其实通过公式 (1) 已经很容易理解了，直接放代码了

function RnkMat = determineRnk(sqDmat)
% calculate the label for each cluster
% 1 for belong, 0 for not belong
N = size(sqDmat,1);
K = size(sqDmat,2);
RnkMat = zeros(N,K);
[~,minIndex] = min(sqDmat,[],2);
positionVec = 1:N;
idxVec = N*(minIndex-1) + positionVec';     % or we can ues this
% idxVec = sub2ind([N,K],positionVec',minIndex); but it is slower than my
% code implementation
RnkMat(idxVec) = 1;
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13

最后就是更新中心点的函数，也是根据EM算法中的公式 (4) 就可以得到了。

function Kmus = recalcMus(X,Rnk)
% get the Kmus from the mean value of the cluster
% mu_k = frac{\sum_n{r_{nk}X_n}{\sum_n{r_{nk}}}
% X: N by D
% Rnk: N by K
% Kmus: K by D
N = size(X,1);
K = size(Rnk,2);
D = size(X,2);
sumCluster = Rnk'*X;    % K by D
numCluster = sum(Rnk)';  % K by 1
normMat = repmat(numCluster,1,D);
Kmus = sumCluster./normMat;
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14

最后是一个小trick在主程序画图过程中的plotCurrent() 函数后面跟着一个停顿函数pause(1) 会在循环过程中产生动态效果，如下图所示（忽略恶心的水印） 

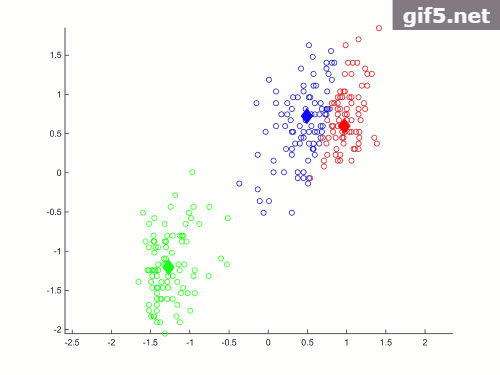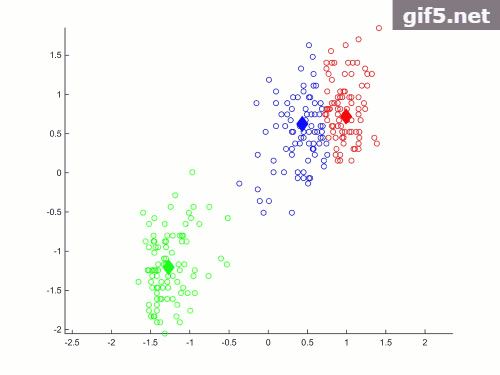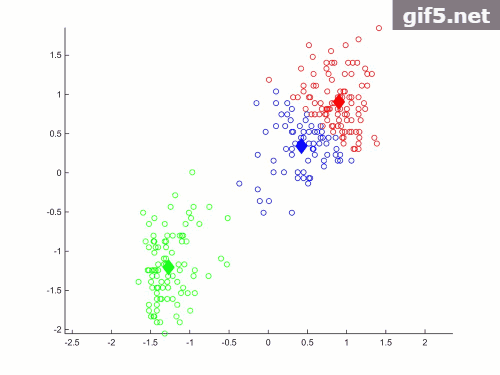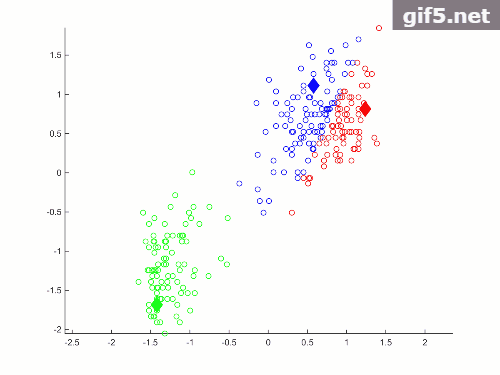
绘图函数是这样的

function    plotCurrent(X,Rnk,Kmus)
[N,D]=size(X);
K=size(Kmus,1);
clf;
figure(1);
hold on;
InitColorMat= [1 0 0;   
               0 1 0;   
               0 0 1;
               0 0 0;
               1 1 0; 
               1 0 1; 
               0 1 1;
               0.5 1 0.5];
KColorMat=InitColorMat(1:K,:);
colorVec=Rnk*KColorMat;
muColorVec=eye(K)*KColorMat;
scatter(X(:,1),X(:,2),[],colorVec)
scatter(Kmus(:,1),Kmus(:,2),200,muColorVec,'d','filled');
axis equal;
hold off;
end
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

结果分析

随着K的变化，整体的距离变化为如图所示，动态变化上图已经展示。 

调试代码为

% KMeans_script
% for i = 1:100
filename = 'scaledfaithful.txt';
%%
K = 2;
k2_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k2_cost = runKMeans(K,filename);
    k2_cost_all = k2_cost_all + k2_cost;
end
k2_cost_avg = k2_cost_all/max_num;
%%
K = 3;
k3_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k3_cost = runKMeans(K,filename);
    k3_cost_all = k3_cost_all + k3_cost;
end
k3_cost_avg = k3_cost_all/max_num;
%%
K = 4;
k4_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k4_cost = runKMeans(K,filename);
    k4_cost_all = k4_cost_all + k4_cost;
end
k4_cost_avg = k4_cost_all/max_num;
%%
K = 5;
k5_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k5_cost = runKMeans(K,filename);
    k5_cost_all = k5_cost_all + k5_cost;
end
k5_cost_avg = k5_cost_all/max_num;
%%
K = 6;
k6_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k6_cost = runKMeans(K,filename);
    k6_cost_all = k6_cost_all + k6_cost;
end
k6_cost_avg = k6_cost_all/max_num;
%%
K = 7;
k7_cost_all = 0;
max_num = 100;
for num_comput = 1:max_num
    k7_cost = runKMeans(K,filename);
    k7_cost_all = k7_cost_all + k7_cost;
end
k7_cost_avg = k7_cost_all/max_num;
%%
cost_K = [k2_cost_avg, k3_cost_avg, k4_cost_avg, k5_cost_avg, k6_cost_avg, k7_cost_avg];
K = 2:7;
plot(K, cost_K, 'rx-','LineWidth', 3)
xlim([2 7])
ylim([20 100])
xlabel('K')
ylabel('cost function value')
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
 
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

虽然无法找到一个最优的K值，但相对来说，k=4或5的时候效果还是不错的。当K=4的时候，收敛图为 

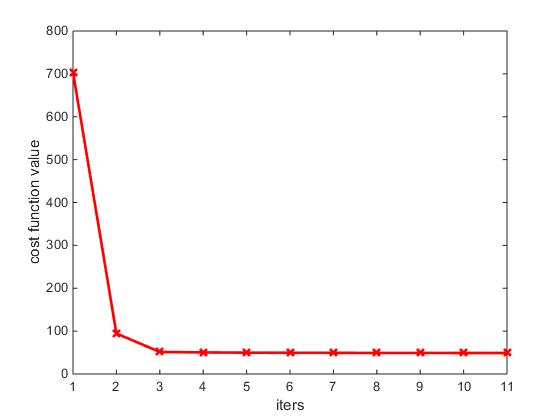
可以发现，收敛的还是非常快的。

总结

本文介绍了聚类算法中常用的K-means算法。从EM算法求解K-means算法问题，并给出了matlab下实现K-means的算法程序。所有的程序和数据均可以从我的github上面下载。希望对大家有所帮助！

---

参考文献

---

1. Array programming in wikipedia 
   https://en.wikipedia.org/wiki/Array_programming ↩
2. 最大期望算法 
   https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm ↩
3. 模式识别与机器学习 
   http://users.isr.ist.utl.pt/~wurmd/Livros/school/Bishop%20-%20Pattern%20Recognition%20And%20Machine%20Learning%20-%20Springer%20%202006.pdf ↩
4. 最大期望算法 
   https://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm ↩