实现本文python程序链接
#K-means聚类算法
#1、相关概念及过程
##1.1、聚类概念
它把n个对象根据他们的属性分为k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。
##1.2、聚类过程
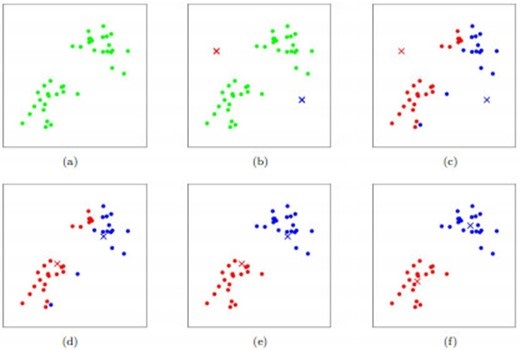
过程的图片描述:
如图所示,数据样本用圆点表示,每个簇的中心点用叉叉表示。
过程的文字描述:
- (a)刚开始时是原始数据,杂乱无章,没有label,看起来都一样,都是绿色的。
- (b)假设数据集可以分为两类,令K=2,随机在坐标上选两个点,作为两个类的中心点。
- (c-f)演示了聚类的两种迭代。先划分,把每个数据样本划分到最近的中心点那一簇;划分完后,更新每个簇的中心,即把该簇的所有数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”,直到每个簇的中心不在移动为止。
#2、注意问题
##2.1、 k数目确定
###2.1.1、重复试验确定法
给定一个合适的类簇指标,比如平均半径或直径;K值设定一定范围,重复试验,看簇类指标的变化规律,找出最合适的K值。只要我们假设的类簇的数目等于或者高于真实的类簇的数目时,该指标上升会很缓慢,而一旦试图得到少于真实数目的类簇时,该指标会急剧上升。
- 簇类指标:
类簇的直径:是指类簇内任意两点之间的最大距离。
类簇的半径:是指类簇内所有点到类簇中心距离的最大值。
平均质心距离:每个簇内所有点到该簇质心距离的平均值
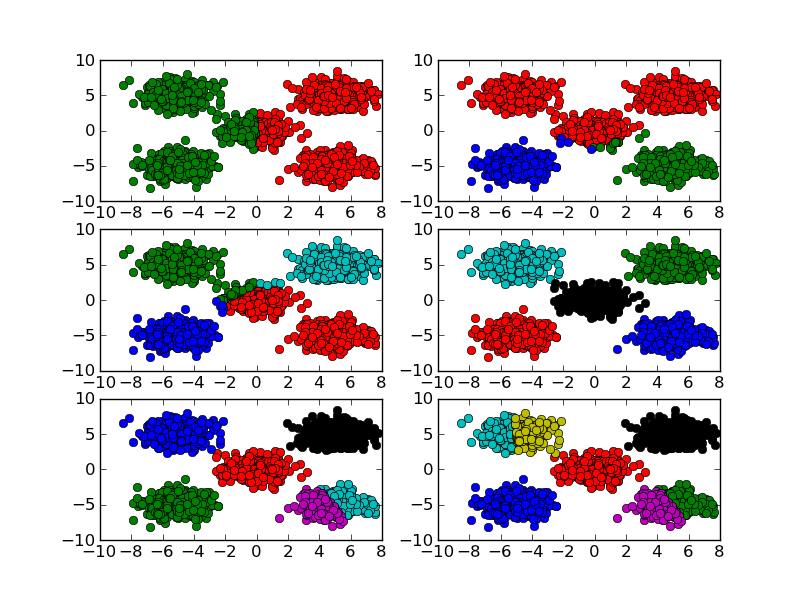
K取值从2到7时的聚类效果:
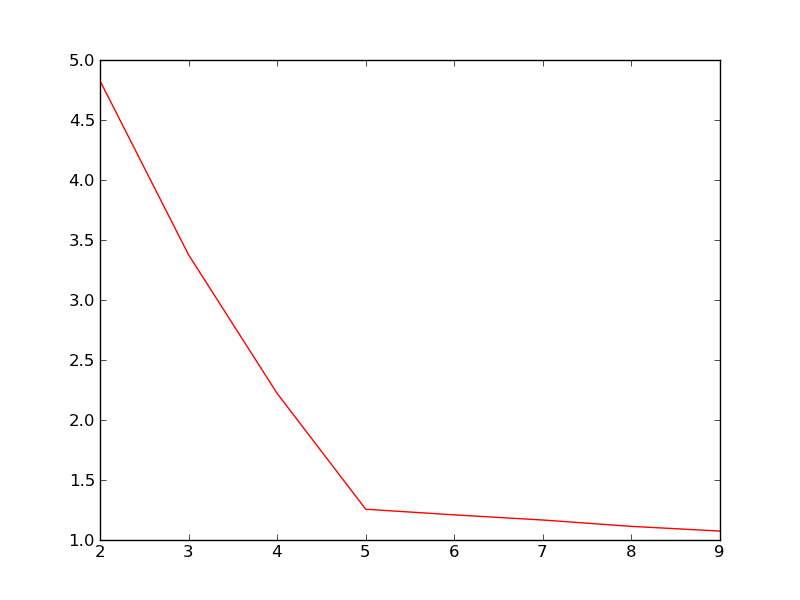
K取值从2到9时的类簇指标的变化曲线:
此处类簇指标是K个类簇的平均质心距离的加权平均值。从上图中可以明显看到,当K取值5时,类簇指标的下降趋势最快,所以K的正确取值应该是5.
###2.1.2、canopy算法
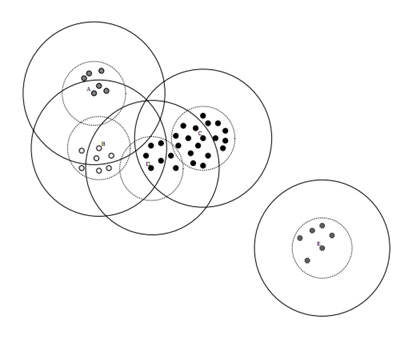
canopy符号含义解释:
canopy过程描述:
1.$ 一组存放在数组里面的数据D$;
2.
两
个
距
离
阈
值
T
1
,
T
2
,
且
T
1
>
T
2
(
大
圈
为
T
1
,
小
圈
为
T
2
)
,
T
1
和
T
2
的
值
可
以
用
交
叉
校
验
来
确
定
;
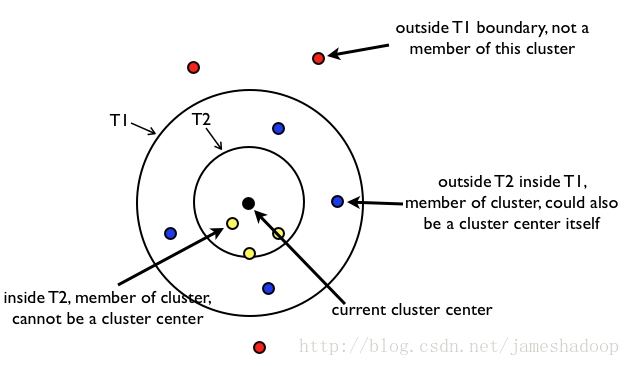
两个距离阈值T1,T2,且T1>T2(大圈为T1,小圈为T2),T1和T2的值可以用交叉校验来确定;
两个距离阈值T1,T2,且T1>T2(大圈为T1,小圈为T2),T1和T2的值可以用交叉校验来确定;
3.
随
机
取
D
中
的
一
个
数
据
d
作
为
中
心
,
并
将
d
从
D
中
移
除
;
随机取D中的一个数据d作为中心,并将d从D中移除;
随机取D中的一个数据d作为中心,并将d从D中移除;
4.
计
算
D
中
所
有
点
到
d
的
距
离
d
i
s
t
a
n
c
e
;
计算D中所有点到d的距离distance;
计算D中所有点到d的距离distance;
5.
将
所
有
d
i
s
t
a
n
c
e
<
T
1
的
点
都
归
如
到
d
为
中
心
的
c
a
n
o
p
y
1
类
中
,
(
注
:
d
i
s
t
a
n
c
e
<
T
1
包
含
d
i
s
t
a
n
c
e
<
T
2
和
T
2
<
=
d
i
s
t
a
n
c
e
<
T
1
)
;
将所有distance<T1的点都归如到d为中心的canopy1类中,(注:distance<T1包含distance<T2和T2<=distance<T1);
将所有distance<T1的点都归如到d为中心的canopy1类中,(注:distance<T1包含distance<T2和T2<=distance<T1);
6.
将
所
有
d
i
s
t
a
n
c
e
<
T
2
的
点
,
都
从
D
中
移
除
;
将所有distance<T2的点,都从D中移除;
将所有distance<T2的点,都从D中移除;
7.
重
复
步
骤
4
到
6
,
直
到
D
为
空
,
形
成
多
个
c
a
n
o
p
y
类
。
重复步骤4到6,直到D为空,形成多个canopy类。
重复步骤4到6,直到D为空,形成多个canopy类。
canopy最终效果:
###2.1.3 层次聚类
层次聚类算法是将所有的样本点自底向上合并组成一棵树或者自顶向下分裂成一棵树的过程,这两种方式分别称为凝聚和分裂。
- 凝聚层次算法:
初始阶段,将每个样本点分别当做其类簇,然后合并这些原子类簇直至达到预期的类簇数或者其他终止条件。
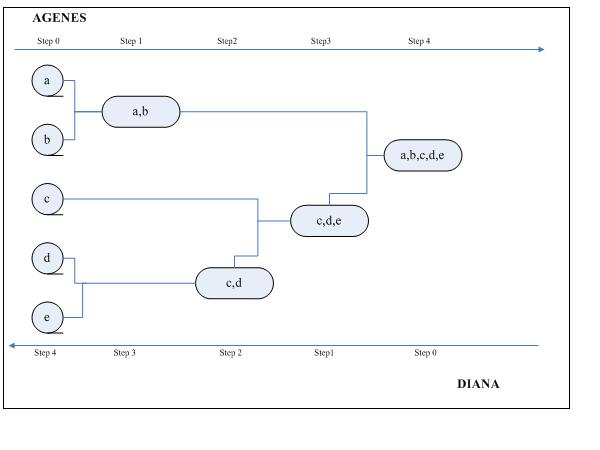
传统的凝聚层次聚类算法有AGENES,初始时,AGENES将每个样本点自为一簇,然后这些簇根据某种准则逐渐合并,例如,如果簇C1中的一个样本点和簇C2中的一个样本点之间的距离是所有不同类簇的样本点间欧几里得距离最近的,则认为簇C1和簇C2是相似可合并的。
- 分裂层次算法:
初始阶段,将所有的样本点当做同一类簇,然后分裂这个大类簇直至达到预期的类簇数或者其他终止条件。
传统的分裂层次聚类算法有DIANA,初始时DIANA将所有样本点归为同一类簇,然后根据某种准则进行逐渐分裂,例如类簇C中两个样本点A和B之间的距离是类簇C中所有样本点间距离最远的一对,那么样本点A和B将分裂成两个簇C1和C2,并且先前类簇C中其他样本点根据与A和B之间的距离,分别纳入到簇C1和C2中,例为4, 因 为 D i s t a n c e ( A , O ) < D i s t a n c e ( B , O ) 那 么 O 将 纳 入 到 类 簇 C 1 中 因为Distance(A,O)<Distance(B,O)那么O将纳入到类簇C1中 因为Distance(A,O)<Distance(B,O)那么O将纳入到类簇C1中
过程如下:
##2.2、初始质心选择
###2.2.1、最大距离选择法
首先随机选择一个点作为第一个初始类簇中心点,然后选择距离该点最远的那个点作为第二个初始类簇中心点,然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点,以此类推,直至选出K个初始类簇中心点。
###2.2.2、预处理法
选用层次聚类或者Canopy算法进行初始聚类,然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。
##2.3、不同距离公式
- 闵可夫基距离:
(2.3.1) d ( X , Y ) = ∑ i = 1 n ∣ x i − y i ∣ p p d(X,Y)=\sqrt[p]{\sum_{i=1}^{n}|x_{i}-y_{i}|^{p}}\tag{2.3.1} d(X,Y)=pi=1∑n∣xi−yi∣p(2.3.1) - 当p=1时,为曼哈顿距离:
(2.3.2) d ( X , Y ) = ∑ i = 1 n ∣ x i − y i ∣ d(X,Y)={\sum_{i=1}^{n}|x_{i}-y_{i}|}\tag{2.3.2} d(X,Y)=i=1∑n∣xi−yi∣(2.3.2) - 当p=2时,为欧几里德距离:
(2.3.3) d ( X , Y ) = ∑ i = 1 n ∣ x i − y i ∣ 2 d(X,Y)=\sqrt{\sum_{i=1}^{n}|x_{i}-y_{i}|^{2}}\tag{2.3.3} d(X,Y)=i=1∑n∣xi−yi∣2(2.3.3) - 皮尔逊相关系数
(2.3.4) ρ X , Y = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] σ X σ Y \rho_{X,Y}=\frac{E\left[(X-E(X))(Y-E(Y))\right]}{\sigma_{X}\sigma_{Y}}\tag{2.3.4} ρX,Y=σXσYE[(X−E(X))(Y−E(Y))](2.3.4) - 余弦相似度
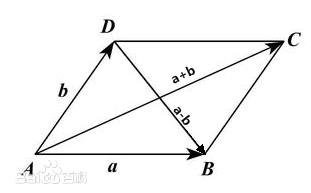
向量加法: A B ⃗ + B C ⃗ = B C ⃗ \vec{AB}+\vec{BC}=\vec{BC} AB+BC=BC
向量减法: A B ⃗ − A D ⃗ = D B ⃗ \vec{AB}-\vec{AD}=\vec{DB} AB−AD=DB
余弦定理: ( a ⃗ − b ⃗ ) 2 = ( a ⃗ ) 2 + ( b ⃗ ) 2 − 2 ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ c o s A (\vec{a}-\vec{b})^2=(\vec{a})^{2}+(\vec{b})^{2}-2|\vec{a}|\cdot|\vec{b}|\cdot cosA (a−b)2=(a)2+(b)2−2∣a∣⋅∣b∣⋅cosA
二次项展开: ( a ⃗ − b ⃗ ) 2 = ( a ⃗ ) 2 + ( b ⃗ ) 2 − 2 a ⃗ b ⃗ (\vec{a}-\vec{b})^2=(\vec{a})^{2}+(\vec{b})^{2}-2\vec{a}\vec{b} (a−b)2=(a)2+(b)2−2ab
根据上面两式得: a ⃗ b ⃗ = ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ ⋅ c o s A \vec{a}\ \vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot cosA a b=∣a∣⋅∣b∣⋅cosA
余弦相似度为: (2.2.5) c o s A = a ⃗ b ⃗ ∣ a ⃗ ∣ ⋅ ∣ b ⃗ ∣ cosA=\frac{\vec{a}\ \vec{b}}{|\vec{a}|\cdot|\vec{b}|}\tag{2.2.5} cosA=∣a∣⋅∣b∣a b(2.2.5)
- 杰卡德相似性度量
(2.2.6) J ( X , Y ) = ∣ X ⋂ Y ∣ ∣ X ⋃ Y ∣ J(X,Y)=\frac{|X\bigcap Y|}{|X\bigcup Y|}\tag{2.2.6} J(X,Y)=∣X⋃Y∣∣X⋂Y∣(2.2.6)
- 杰卡德距离
(2.2.7) J δ = 1 − J ( X , Y ) = ∣ X ⋃ Y ∣ − ∣ X ⋂ Y ∣ ∣ X ⋃ Y ∣ J_{\delta}=1-J(X,Y)=\frac{|X\bigcup Y|-|X\bigcap Y|}{|X\bigcup Y|}\tag{2.2.7} Jδ=1−J(X,Y)=∣X⋃Y∣∣X⋃Y∣−∣X⋂Y∣(2.2.7)
##2.3、质心的计算
一般来说,求点群中心点的算法你可以很简的使用各个点的坐标的平均值。
c i = 1 m ∑ x ∈ C i x c_{i}=\frac{1}{m}\sum_{x\in C_{i}}x ci=m1x∈Ci∑x
##2.4、终止条件的确定
一般是目标函数达到最优(前后两次迭代误差在给定范围内)或者达到最大的迭代次数即可终止。对于不同的距离度量,目标函数往往不同。当采用欧式距离时,目标函数一般为最小化对象到其簇质心的距离的平方和,如下:
误差平方和(sum of the squared error,SSE)
S S E = ∑ i = 1 K ∑ x ∈ C i d i s t ( c i , x ) 2 SSE=\sum_{i=1}^{K}\sum_{x\in C_{i}}dist(c_{i},x)^2 SSE=i=1∑Kx∈Ci∑dist(ci,x)2
SSE为所有点到其所属簇质心的距离的总和。
c i = 1 m ∑ x ∈ C i x c_{i}=\frac{1}{m}\sum_{x\in C_{i}}x ci=m1x∈Ci∑x
对簇内点在每个维度求平均值,为质心。
| 符号 | 描述 |
|---|---|
| x | 对象 |
| C i C_{i} Ci | 第i个簇 |
| c i c_{i} ci | 簇 C i 的 质 心 C_{i}的质心 Ci的质心 |
| c c c | 所有点的质心 |
| m i m_{i} mi | 第i个簇中对象的个数 |
| m m m | 数据集中对象的个数 |
| K K K | 簇的个数 |






















 1142
1142

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








